Часто в олимпиадных задачах, чтобы оценить асимптотику алгоритма, требуется знать примерное число делителей поступающего на вход числа. Точнее, требуется знать максимальное число делителей среди всех чисел до, скажем, миллиарда.
Самая грубая оценка - O (sqrt(N)), а именно, не более двух квадратных корней из N.
Но часто это оказывается слишком грубой оценкой, неоправданно завышенной.
Обычная используемая мной оценка - O(кубического корня из N). Эту таинственную оценку я услышал когда-то давно от кого-то, и никогда её не понимал, но пользовался ей, и она работала.
Совсем недавно мы делали стресс-тест, и на числах до миллиарда она подтвердилась - число делителей не превосходит двух кубических корней из числа. Этого "доказательства" вполне достаточно, чтобы и дальше применять эту оценку на практике. Но найти ей математическое объяснение ну никак не получалось.
Сегодня в очередной раз решил поискать на эту тему в интернете. На этот раз нашёл то. что нужно, на удивление быстро: en.wikipedia.org/wiki/Divisor_function. Здесь много всякого интересного, но вот главная вещь, поразительная для меня формула:
"для любого eps>0 выполняется: d(n) = o(n^eps)"
Выходит, на самом деле число делителей ведёт себя на бесконечности не только лучше квадратного, кубического и прочего корней из числа n; оно вообще является субполиномиальной величиной!
Другие оценки:
- Wigert: "d(n) ~ n ^ (log2 / log log n)" (ну я примерно передал порядок, на самом деле там формула посложнее)
- Дирихле: "СУММА_{i=1..n} d(i) / n ~ log n + 2 gamma - 1"
P.S. Некоторым это может показаться бояном, но я знаю, что многие до сих пор даже не знают, что число делителей меньше квадратного корня, не говоря уже о таких "крутых" оценках :)
P.P.S. Для олимпиад, где обычно в таких задачах мы имеем дело с числами до 10^9 - 10^12, эти оценки малополезны (здесь надо по-прежнему брать корень кубический), но они интересны чисто как математический факт.











было бы очень круто, если б такие лекции появились на codeforces в электронном формате. И вообще теоретический раздел, думаю, был бы очень полезен и интересен.
ваши слова реализованы
то есть например у числа 2^5*3^4*7^2 будет количество делителей: 6*5*3
Вообщем : длинная арифметика в факторизованном виде.
<delete>
Часто бывает нужна оценка суммы количества делителей чисел с 1 до n. Помогает оценка nln(n). Кому интересно вкратце рассказываю как она получается. Каждое число d, такое что 1<=d<=n считается как делитель у n/d чисел (среди чисел от 1 до n кратные d:d,2d,3d.... Их n/d штук) То есть в итоге сумма количеств подсчитанных делителей равна n/1+n/2+n/3+....+n/n (если быть точным то везде округление вниз) В итоге если n вынести за скобочку получается n(1/1+1/2+1/3+...+1/n)=n*h(n), где h(n) — n-ное гармоническое число. (Оно приблизительно равно ln(n). Те кому интересно об этом можно почитать http://ru.wikipedia.org/wiki/Гармонический_ряд или в книге Кнута "Конкретная математика").
суммы количества делителей? суммы делителей?
Сумма d(k) по всем k=1..n. Оценка очень известная. К сожалению, решить задачу "разложите все числа в диапазоне [a;b] на множители" за O((b-a)*log(max(a,b)) это не особо помогает.
Объясняю что я имел ввиду. С одной стороны суммарное количество делителей можно посчитать в лоб (для каждого числа от 1 до n можно найти количество делителей этого числа, а потом суммировать n полученных чисел) С другой стороны можно для каждого числа от 1 до n посчитать в скольких числах (от 1 до n) он является делителем, а потом суммировать уже эти числа. В этом случае получается оценка на то что хотели. Как бы двойной подсчет. Согласен, немного криво написал.
Не, cooler правильно понял, что я не понял определение того, что мы хотим посчитать.
Разве нельзя решить эту задачу за O(sqrt N)?
Сумма количества делителей чисел от 1 до N — количество точек под гиперболой xy=N. (рассматриваем первую четверть)
Эта задача решается за корень — бежим по i от 1 до sqrt(N) с округлением вниз и прибавляем к ответу 2*(N/i с округлением вниз).
Так мы посчитали количество точек под гиперболой с координатой x<=sqrt(N) и количество точек с координатой y<=sqrt(N). Очевидно, все точки уже подсчитаны, но некоторые дважды. Избавимся от лишних, вычтя (sqrt(N) с округлением вниз)^2.
Вроде бы все. Вернусь домой, приведу в порядок формулы.
Да ваш способ в целом тоже верен. Но он не дает более хорошей оценки на суммарное кол-во делителей чисел от 1 до n (видимо n*ln(n) это точная оценка), а цель была именно в этом.
А зачем было стрессить до 10^9, если можно легко и непринужденно посчитать на достаточно большом отрезке [a;b] (a,b <= 10^18) точное значение min(k/(d(k))^3)?
Но ведь задача "найти максимальное количество делителей среди всех чисел до K" вроде как решается значительно более быстрым алгоритмом, чем задача "найти количество делителей конкретного числа K". Так зачем тогда называть тему "Число делителей числа N", а говорить о промежутке?
Кстати, совсем на днях закончился 3-й тур НетОИ ( http://www.olymp.vinnica.ua/index_ua.php?lng=ru&cid=1155 ), так там задача "найти максимальное количество делителей среди всех чисел до K" (до 1019) оказалась одной из самых решаемых...
(Sorry, не уверен, должно ли в ссылке быть именно 1155 или какое-то похожее, а сайт сию секунду under constuction...)
А что там решать то, если все уже давно решено. Возьмем числа с наибольшим количеством делителей тут, ну и если вообще ничего делать не охота, то возьмем само количество делителей тут. Побольше бы таких задач на интернет олимпиадах...
Для тех, кому интересно, доказательство субполиномиальности d(n).
zadacha ochen prostaya no hitraya!!! ))))
Количество и суму делителей можно найти за факторизацией числа. Т.е. за разложением числа на простые делители. Пусть p_i количество простого делителя a_i.
Количество делителей
(p_1+1)*(p_2+1)*...*(p_n+1), где n это количество простых делителей.
Сума делителей
(a_1+a_1^2+...+a_1^p_1)*(a_2+a_2^2+...+a_2^p_2)*...*(a_n+a_n^2+...+a_n^p_n)+1
so what?
Совсем недавно мы делали стресс-тест, и на числах до миллиарда она подтвердилась - число делителей не превосходит двух кубических корней из числа.σ0(6240) = 48, в то время как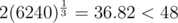 . Не работает, переделывай
. Не работает, переделывай
5 лет числа перебирал?
Раз уж на то пошло, σ(6) = 4, 2(6)1 / 3 = 3.63 < 4.
Не, здесь "числа" — это миллиарда. Следует читать так:
Совсем недавно мы делали стресс-тест, и на числах до миллиарда она подтвердилась - число делителей не превосходит двух кубических корней из этого самого миллиарда.Такое утверждение не соответствует используемой оценке же.
Зато его можно использовать. Если сказано, что n <= 1000000000, а моё решение работает за sigma(n)^2, то оно зайдёт, так как число операций будет не больше 2000^2 = 4000000. Не важно, что при каких-то значениях n оно будет работать за n^2 (при этом n маленькое).
Вот оптимальные оценки для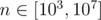 для различных констант от 2 до 10:
для различных констант от 2 до 10:
Также следует отметить, что равенство в последних трех неравенствах достигается на числе 4324320 = 25 × 33 × 5 × 7 × 11 × 13 — у него 384 делителя.
Как в фиолетовые упал, так сразу перестали плюсы ставить?
Добро пожаловать в клуб!
Поскольку никто так и не написал какая же там константа при оценке кубического корня. Проверил числа до 100 миллионов. Количество делителей не больше 3.52729 кубических корней их этого числа. Оценка достигается на числе 2520. По факту можно просто считать, что точно не больше 4 кубических корней из числа.
Bad previous comment