vovuh's blog

Codeforces Round #531 (Div. 3) Editorial
By vovuh, history, 6 years ago, In English

1102A - Integer Sequence Dividing

Tutorial
Solution 1
Solution 2

1102B - Array K-Coloring

Tutorial
Solution

1102C - Doors Breaking and Repairing

Tutorial
Solution

1102D - Balanced Ternary String

Tutorial
Solution (Vovuh)
Solution (PikMike)

1102E - Monotonic Renumeration

Tutorial
Solution

1102F - Elongated Matrix

Tutorial
Solution 1
Solution 2
  • Vote: I like it
  • +32
  • Vote: I do not like it

Comments Comments (30)
| Write comment?
»
6 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Hey awoo , can you explain your solution for D ? I was thinking on similar lines but messed it up in placing 1's.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    I thought of it the following way. You start with either a single amount greater than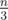 or a single amount less than 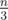(the both zeros case is trivial).

    Case 1: Replace some of characters x with other characters. I just assumed that if the character to replace with is smaller than x then you should replace some prefix of x occurrences and if it's greater than x then suffix of occurrences. It should be easy to prove. Then the order of applying functions matters only if x = 0 or x = 2 (determining the order is trivial).

    Case 2: Replace some character with character x. Following the same ideas you also determine when prefix/suffix is the best and the order of application.

    The code itself is really self-explanatory. I believe that the proof is the hardest part of it.

    → Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Hey vovuh , can you explain about E? What are the possible answers for 4 1 3 3 7

There should be only three 3 closed subsegments. So answer = 2^2 = 4 But possible arrays for b is - 0 0 0 0 - 0 0 0 1 - 0 1 1 1 I can't think of the fourth answer as 0 1 1 0 can't be the answer Thanks in advance:)

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    0 1 1 2

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Thanks:) Got it So can we say that if there are m subsegments. Then answer will be 2^(m-1), Because left most subsegments have the value 0 and all other subsegments have two options either have value of their left subsegment or increase previous value by 1 Is it correct

      → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Shouldn't the answer be 8 (2^3) because there are four closed segments ( [4], [1], [3,3], [7])

    The eight renumerations are as follows :
    0 0 0 0 0
    0 0 0 0 1
    0 0 1 1 1
    0 0 1 1 2
    0 1 1 1 1
    0 1 1 1 2
    0 1 2 2 2
    0 1 2 2 3

    → Reply
»
6 years ago, # |
← Rev. 3   Vote: I like it +7 Vote: I do not like it

We can also have another approach for Problem B (1102B - Array K-Coloring), which is also quite nice, and runs only in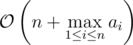 time complexity.

First of all, obviously if any value x exists more than k times, then there will be no coloring scenarios possible.

We'll traverse the array linearly from left to right, and color an element right after traversing it.
Let's initiate an array cnt storing the frequency of elements, a.k.a. cnt[i] is the number of elements with value i found so far.
Also, let's denote Max as the maximum index of any used colors. Initially Max = 0.
For each i (1 ≤ i ≤ n), we'll do the following:

  • Let's denote x = ai. Increase cnt[x] by 1.
  • Normally, color the i-th element by the color with the index equals to the current value of cnt[x]. Obviously, it will guarantee that no two elements with equal value will have the same color.
  • Since we have to color the array with all colors from 1 to k, we should keep in mind if the current element and all following it can be colored using the unused colors (which means all colors z with Max + 1 ≤ z ≤ k). So if it's possible (we can mathematically figure out the criterion as Max + (n - (i - 1)) = k), instead of coloring follow the above plan, we'll follow the current element (and, as a chain reaction, all elements following it, using the same plan) using the color with index Max + 1. The criterion of all equal-value elements having pairwise different colors is still obviously guaranteed, since the color we just used is something haven't been used before, and the situation shows that we'll use that color only once (the next element (if exists) will be colored by the next color, until Max reaching k, which also marks the end of the array).
  • Remember to update Max before traversing the next element.

Since this solution depends on the value of elements in a, so in case they're huge integers (maybe Int64 or such), we can use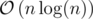 map data structure to implement cnt array — the complexity would be .

The explanation seems long, but the it's mainly my explanation and proof for it. The implementation itself is pretty neat if you might ask. You can see it here: 48189557

P/s: I realized this comment of mine is longer than the source code itself :D

→ Reply
»
6 years ago, # |
  Vote: I like it +5 Vote: I do not like it

This Div 3 contest was quite interesting.

My code to D does a little more work than the editorial solution but I think my explanation might be a little easier to understand. :)

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +2 Vote: I do not like it

    I solved it using these steps link.

    1. try to fill '0' from the left side of the array.
    1. fill '2' from the right side of the array.
    1. now for filling '1' if we replace '0' then do this from the right side of the array and if we are replacing '2' then do form left side of the array.
    → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    nice approach

    → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    Thanks a lot for sharing your approach and solution. It made it look very simple.

    → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Anyone help me to find the error in problem D? Why my solution 48190526 is getting WA in TC 13.

→ Reply
»
6 years ago, # |
  Vote: I like it +2 Vote: I do not like it

I think that my solution for E is a little bit easier to understand 48143299

1) a[i] == a[j] <=> b[i] == b[j] We can notice that our b value cannot become less with index increase, so if we are between two equal numbers, we can't increment our function value, because when we will come to this number (which is equal for our first number), we can't support a[i] == a[j] <=> b[i] == b[j].

So, we simply find the first and the last occurrences for every number in a[] (occur[n] = {first_oc, last_oc})

ans = 1 (because we can always make b[] = [0] * n);

Let's keep in memory value named depth, which will represent enclosure rate (just like in bracket sequences)

Simply iterate from 0 to n — 1:

if occur[N].first == i: depth++;

if occur[N].second == i: depth--;

if our depth is zero, we can put b[i + 1] = b[i] or b[i + 1] = b[i] + 1, so our ans become doubled.

I think that my explanation is incomprehensible, so you can check out the code! 48143299

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In solution 1 of F, how do you ensure that the Hamiltonian path starts with i? I can see that you have changed the initial values in the DP for that but I am still not able to understand that. Can you please explain a bit?

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it +3 Vote: I do not like it

    I just make it overly unoptimal to start from any other vertex. That way any path that could have made the overall answer better will start from the vertex I want.

    → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Where i can read about Hamiltonian path?

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Could somebody please help me figure out why my O(n) solution is getting TLE for E? https://codeforces.me/contest/1102/submission/48244158

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Try using 'set' instead of 'unordered_set'. I had the exact same problem of getting stuck on test 48 and changing to 'set' solved the issue. It seems that this particular test is a anti-hashing testcase made to stop people who used 'unordered_set' in their code. Relevant: https://codeforces.me/blog/entry/62393

    → Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

for the problem F's first solution, can any one explain why the initialization is dp[1 << j][j] = (j == i ? INF : 0); instead of dp[1 << j][j] = (j == i ? 0 : INF); As we assume the i is the starting point, then any other node except i should be initialized to INF?

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Yes, i is the starting point. But we are looking for the minimum weight of the Hamilton cycle. Setting dp[1 << j][j] (j != i) to 0 means that, the minimum weight for the other starting points are already 0, so that function calc won't consider them anymore. 

    dp[mask][v] = max(dp[mask][v], min(mn1[u][v], calc(mask ^ (1 << v), u)));
// if the return value of calc(mask ^ (1 << v), u) is 0, 
// it won't in anyway be able to improve dp[mask][v],
// so in this way other starting points are ignored.

    And INF is the normal initialization, since we are looking for minimum weight and in status 1 << i, there is only one point i and no edge (weight) has appeared.

    → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In F, solution1, what is the significance of

forn(j, n) dp[1 << j][j] = (j == i ? INF : 0);

in the main function's last nested for loop?

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    It ensures that path starts with i.

    → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

vovuh I have completely understood solution 1. But got stuck in solution 2. can you please explain what array dp ,used, g and function check and calc are doing in 1102F — Elongated Matrix SOLUTON2

→ Reply
»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

The second solution of F can be optimised to O(2^n . n. log(MAXN))

As it is possible to check for hamiltonian path in O(2^n . n) time

https://codeforces.me/blog/entry/337

→ Reply