Lets discuss problems.
How to solve A Alice and path, F Fizz and Bazz, J Cubic path?
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 156 |
| 6 | adamant | 152 |
| 6 | djm03178 | 152 |
| 8 | Qingyu | 151 |
| 9 | luogu_official | 149 |
| 10 | awoo | 147 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Feb/20/2025 19:55:21 (f1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











A: the last step is reversed with 'b'. The others are obtained by reversing the string and replacing 'l' with 'r' and vice versa.
F: if ai isn't divisible by 3 — print 'B', by 5 — print 'F'. Otherwise print 'B'. The probability of you being correct on divisible by 15 numbers is enough to make less than 1200 mistakes.
J: code bruteforce and either hardcode all answers or optimize it.
In A, I got WA, but tried this idea: delete consecutive 'r' x 6 and 'l' x 6 and 'b' x 2 as they don't change a triangle and direction. Then for any number (0 .. 5) of consecutive 'r' or 'l' change it to the same letter concatenated 6 minus that number times. Then reverse string. Finally append 'bb'. E.g.
lbrrrr->rrblllllbb. Can you write a test against this approach?Upd. Thanks Gassa for colaboration. We found that my program (but not an approach mensioned) failed at test case like
LLLLRRRRRRLLLL, because I useds/(L|R)\1*/ $1 x ( 6 - length $& ) /egi(here $& stays for full match, $1 — for match inside parentheses, \1 — for backreferencing to $1, modifiers: e — evaluate, g — many times, i — ignore case), and after deletion of 6R, it becomes 8L (which is >0..5). Correct way was to use match limits:(L|R)\1*->(L|R)\1{0,4}(and then deletion of 6L/6R/2B and addition of 2B become redundant).print scalar reverse <> =~ s/\n//r =~ s/(L|R)\1{0,4}/ $1 x ( 6 - length $& ) /egir;(dollar signs are replaced to non-ascii because no latex formatting)B, C, D?
C. Anti-Distance. One can realize that the answer distance is |x1 - x2| + |y1 - y2| plus some moves (even number) for getting around some boxes. The need for getting around boxes arises when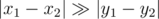 or
or 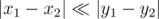 .
.
Need for overturning arises in four directions, all four are symmetric (by rotating 90 deg).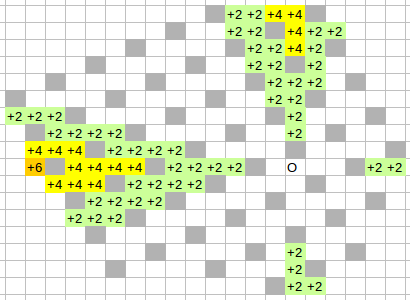
One can simplify searching directions from 4 to 2 by swapping coordinates of O and X if e.g. x1 > x2.
One can rotate coordinates of O and X if e.g. y1 > y2. After rotation, one needs to adjust box-pattern. Note that box-field is self-repeating 5x5 squares. So one can move both O and X by any axis (<5 cells) until it gets adjusted. This simplify searching downto only 1 pair of two cases.
When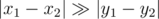 , one can move X closer to O without overturns by decreasing delta x and delta y. When delta y is decreased by 1, then delta x is decreased by 2 or by 3 depending on a direction of an approach (as patterns differ). When delta y becomes zero, one needs to calculate a number of boxes between xleft and xright and multiply by 2 (as it is a distance of getting around).
, one can move X closer to O without overturns by decreasing delta x and delta y. When delta y is decreased by 1, then delta x is decreased by 2 or by 3 depending on a direction of an approach (as patterns differ). When delta y becomes zero, one needs to calculate a number of boxes between xleft and xright and multiply by 2 (as it is a distance of getting around).
Your Spoiler 1 is a nice visualization of the problem!
B: do sqrt decomposition, in each block calculate prefix and suffix sums and also find sum for each group of consecutive blocks, also make a segment tree (it's ~ 3n queries). Then for big queries do a lookup (it's 2 operations) and for small queries use a segment tree. It may be too much still, but if you shuffled everything first, then expected number of small queries is small and this gets AC
С: rotate(and shrink) everything a little bit, so that centers of unusable cells are in integer coordinates. You get some bigger "squares". Suppose you want to go from some cell in the square (x1, y1), to the "same" cell in square (x2, y2). Not proved fact: you need 4min(|x1-x2|, |y1-y2|))+3(max(|x1-x2|, |y1-y2|))-min(|x1-x2|, |y1-y2|))) actions. Now, make a bfs near one or both of starts and then use the formula.
D: solution if those were programs (I do not know to code this as functional scheme in finite time).
We have log n iterations where we have some graph and exchange log n bits: first program gives an id of vertex v1 in the clique that has least degree, second program gives an id of vertex v2 in the clique that has biggest degree. After that each program calculates subgraph that has only vertices that are connected to v1(and v1) and that are not connected to v2 (and v2). 3 cases possible
deg(v1) > deg(v2). Then there's no answer
deg(v1) <= n/2. Then graph becomes ~2 times smaller
deg(v2) >= n / 2 Then graph becomes ~2 times smaller
Stopping condition should be checked more carefully,
tunyash, I wonder if you had a simpler solution than this, and how long it took to write one if not.
The problem itself (if you take out the binary circuits) is well-known communication complexity problem (I've hoped that it is only moderately known in the competitive programming community). I wanted to give a problem based on it for a long time and before the championship I thought that I can do it. Unfortunately the way I initially planned failed and there were only two days before the championship so I've decided to do everything in the straightforward way.
I've cursed this idea, the problem and myself many times when I implemented the solution for about 4 hours and then debugged it for another 3 (it is so awfully unpleasant to debug a circuit inside communication protocol).
I've hoped that the participants will come up with something easier to implement than me and that since they code much faster they will make it :) Apparently it was way too tedious.
I am sorry that I've spoiled a nice problem with this gargantuan implementation, but there are a lot nice ideas in communication complexity and probably better ways to wrap it as an ACM problem.
B: Separate the array into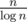 blocks of length
blocks of length  . Compute the operation on all prefixes and suffixes of the blocks. After that build a new array b of length
. Compute the operation on all prefixes and suffixes of the blocks. After that build a new array b of length 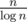 where
where 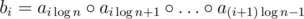 .
.
One can build a data structure with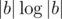 initial operations such that the data structure could compute
initial operations such that the data structure could compute  in 1 operation for any
in 1 operation for any 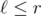 . I denote this number as
. I denote this number as 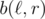 and respectively
and respectively 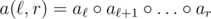 .
.
Assume for now that we have a data structure like this. How to solve the initial problem? In order to find the answer for the query x1, ..., xk you can compute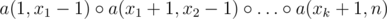 .
.
The needed structure can be constructed as follows: divide the array A in two halves and compute the operation on the suffixes of the first half and on the prefixes of the second one. With that we can compute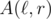 if
if 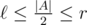 in one operation. The next step is to recursively construct the structure for the both halves of the array. The depth of recursion is
in one operation. The next step is to recursively construct the structure for the both halves of the array. The depth of recursion is 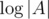 therefore the complexity is
therefore the complexity is 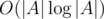 .
.
The only part we did not cover is how to deal with the situation when we need to answer a query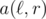 and both
and both 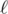 and r are in the same block. How can we deal with it? We can randomly shuffle the array. After that one can compute the expected number of queries for the same block and convince themselves that it is o(n).
and r are in the same block. How can we deal with it? We can randomly shuffle the array. After that one can compute the expected number of queries for the same block and convince themselves that it is o(n).
what if both l and r in the same block?
I've written a short paragraph about it in the end. The key idea is that in this problem you can shuffle the array arbitrary and the expected number of queries inside blocks is very low (I think it is line O(1)). That is the reason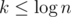 .
.
Yep, we actually did that too in our solution, just wanted to check if there was another idea for that.
I've just splitted everything into blocks by 8 elements (for 2000), and then you can just build the segment tree inside each block
Or array of size 5, and count all subsegments of it.
I guess I was the one stupid enough not to consider random shuffling, here is my ugly solution which works without random:
Do a sqrt-decomposition, for each block calculate prefix- and suffix- sums, for each segment of blocks also compute a sum. Total number of queries to do it is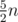 . If segment is not inside one block, we will answer it in 2 queries. For each block build the same sqrt-decomposition. We already spent 5n operations which is not great. But we can divide initial sequence into
. If segment is not inside one block, we will answer it in 2 queries. For each block build the same sqrt-decomposition. We already spent 5n operations which is not great. But we can divide initial sequence into 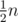 pairs (using
pairs (using 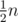 queries), and then build sqrt-decompositions on array of size
queries), and then build sqrt-decompositions on array of size 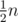 using only
using only 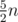 queries, so we have n more queries to spend on the data structure.
queries, so we have n more queries to spend on the data structure.
If segment is not inside smallest block, we will spend only 2 queries to answer it. One can calculate, that smallest blocks will be of size not more than 6, therefore segments strictly inside them will be of size not more than 4. We could answer them in 3 queries, but that's too much, so we will spend our n queries to calculate operations between neighbors. Now we can answer each segment in 2 queries.
It looks like because I divided initial sequence into pairs, I will have to do 2 more queries per segment. But that's not true: borders of my segments are x and x + 1 where x is deleted position, one of these borders is even. So, I will have to do 1 more query per segment (amortized). And 1 more query to unite the answers.
Is anyone interested in even more weird solution?
For simplicity let's assume that n is divisible by 35. Let's precompute the answer for each interval [l, r) such that:
We need (11 / 7)n + (1 / 5)n + (n / 35)2 / 2 ≤ 4n opertaions to get these values. Then, since any interval can be written as a disjoint union of at most 5 of these intervals, we need only 4 operations per query.
That is kinda cool :)
But don't you have to combine answers from segments afterwards, which means that you have to do in no more than 3 operations per segment?
Hmm, yes, I completely forgot about that. I guess I was just lucky.
I participated in the round and used an idea almostly the same with yours, but mine solution uses one less operation per segment.
Do a sqrt-decomposition, but make sure that every block has a length divisible by $$$4$$$. Then divide the blocks into even smaller blocks of length $$$4$$$. For every small block of length $$$4$$$ calculate all subsegment sums, using $$$6$$$ operations. Then use $$$2$$$ more operations to calculate the sum without the second or third element. Since for every two adjacent segments we query there is one missing element, we could use the pre-calculated value for both the segments. If there are more than one missing element in one block of size $$$4$$$, we can use brute-force to calculate the sum in that block. This method uses less than $$$4$$$ operations per segment, no matter how big k is and also doesn't rely on random.
D's idea is cute, but looks close to impossible to code in limited time.
I would be nice if you could write a program, not a boolean scheme.
it would be rather easy problem, though
Moreover, it would be well-known problem. "Included in textbooks on communicational complexity"-level of well-known.
Well, I think it is not really well-known in this community so it'd be nice to spread such ideas this way. I would better give the problem without making it implementation disaster.
I agree that the problem is nice and unusually "CP-style". So, yes, it was nice to see it :)
In problem A, there's the string reversing solution, already mentioned by awoo, and there are coordinate solutions, using either Cartesian coordinates or some integer lattice coordinates. Here is another short solution which was not yet mentioned.
1. Suppose that processing the whole input makes an overall change of direction. As each turn is a multiple of 60 degrees, the overall change of direction is also a multiple of 60 degrees. Here's the trick: no matter what was the input, repeating it 5 more times, for a total of 6 times, brings us to the starting point.
2. How do we know whether the direction has changed? Turns out that any input of odd length is fine: it changes the initial direction by either 60, 180, or 300 degrees. So, if the input is of even length, add one more arbitrary step to make it odd, and then proceed with the solution above.
The code is here.
Elegant solution!