Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
| Название |
|---|



Will the tutorial for Div 1-E be available in the future? Edit: it wasn't available just for a few minutes.
in c why we have increased size by 1 and multiply and in last subtract 1 please anyone give me proof
Hey. As for first question. In every block of "a" we can take 1st or 2nd, or 3rd or 4... char "a", or take nothin, so for every block of "a" we have block_a.size+1 cases. To get all global cases answer, we should multiply (block1_a.size+1)( block2_a.size+1)...() But we should ans-=1; because we got one case where we didnt take any "a" in this string.
can someone who can give proof of C ????
Div 2 C:
It doesn't depend at all if there exists any letter other than a or b in the given string. You can for sure ignore those letters, so the editorial says to erase them. Now, what you have is a string consisting only of a and b's. Also two consecutive b's can be merged as one. So your final string will look something like (a...a)b(a...a)b(a...)...
You can now consider this problem as sum of all possible product of subsets of a given set, where each element in the set is the number of a's delimited by b.
For example: In the string "aaabaabaaab", set formed will be {3,2,3,0} (0 can be ignored). Now if you have a set {a1,a2,...,aN}, then sum of all possible products of this set is equal to (1+a1)*(1+a2)*...*(1+aN)-1.
Proof:
Write the required answer as follows:
S = Sum of products of subset with (size=1)+(size=2)+...(size=N)
S = (a1+a2+...aN)+(a1.a2+a1.a3......+aN-1.aN)+...+(a1.a2.....aN)
After factorization,
S = (1+a1)(1+a2)...(1+aN)-1
Hope it helps..:)
It is really helpful for me thanks!!
if you don't understand the math here is my dp solution code
Basically dp[i] stores the number of valid subsequences from first i characters of the string. If the current character is not a then dp[i]=dp[i-1] otherwise we need to find the index of rightmost a to the left of i such that at least one b follow that a then dp[i]+=dp[index]
Hey, can anyone explain why do we need to increase the blocks size by 1? :p (Div2 — C)
Because if we have x 'a' symbols in the block we can pick the first 'a' from this block or the second 'a' or the third or ... or the n-th or we can just not pick any of 'a' from the block.
For a given block you need to decide the number of ways to pick an "a". As it is possible that you do not choose any "a" from that segment we need to add 1 to each segment. Addidtionally you'll be required to subtract 1 from your thus obtained answer as it includes the case where no "a" is selected in all the segments and thus an empty subsequence.
a + b + ab = (1+a)(1+b) -1; a + b + c + ab + bc + ac + abc = (1+a)(1+b)(1+c) -1 in this fashion we can calculate our ans i.e sum of product of every possible combination
Suppose we have a string aaabaabaaa which can be represented by set {3,2,3} which represent 3 consecutive a's followed by b, 2 consecutive a's followed by b and 3 consecutive a's. Now from the set {3,2,3} to choose a subsequence we can choose any one of the first 3 a's and we also have an option to choose non of the a's, therefore we have total (3+1) ways of choosing the first element in our subsequence, similarly for each consecutive a's we have one more way of choosing element from it i.e to choose nothing from it. Thats why we decrease total ways by 1 as it includes complete empty sequence where we chose nothing from all sets. Hope it clears your doubt.
As a comment on problem Div1-B : consider the trie of all strings that made of only 'a' and 'b' chars, It's a complete binary tree of height n. actually we should choose k leave of this tree such that the strings of these leaves be in the range [s,t] and the minimal sub-tree that consists these leaves and the root of the trie is as large as possible the final answer is the size of this sub-tree!
Ok! now we greedily add leaves and compute the answer! (counting,bfs or...) Now we can solve the more general case of this problem! :)) (for example: each string consists lowercase English letters!)
There is another approach for problem D (div 2), A (div 1), which consists on reducing to longest path on a tree as follows:
First of all, for each node 1, ..., n attach an extra node just connected to it. For example, let's attach node n + 1 to node 1, n + 2 to node 2,..., 2n to node n. So now we have a new tree with 2n vertices. All the new nodes and edges will have weight zero. So let's call this graph G.
Now, construct another graph G', which has the same set of vertices and the same edges of G. We let all the weights of the vertices of G' be zero. But we let the weight of an edge in G' be the mean value of the weights of their vertices in G minus the weight of the edge in G. So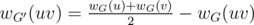 .
.
Now, if you look at this properly, when you consider a path between two nodes in G', it collects in each edge half of the value of the nodes involved and decreases according to the original value of the edge. So, what we want now is simply the longest possible path on a tree. This is a classical problem, and can be solved with a dfs (be careful, because here the weights may be negative!).
Can someone explain C with dp approach ?
I did using 3 parameters:
i: the current position in the string;
n: meaning if i have or not a 'b' in the current subsegment;
p: meaning if i already formed a valid subsegment.
Basicaly,
if the current caracter is 'a' and i already have a 'b' i can start a new subsegment or continuos a previous;
or, if the current caracter is 'a' and i don't have a 'b', i can just continuos the subsegment;
if is 'b' i set that i have a 'b';
else, i just go.
submission
Hello, In your approach as far as I can understand when n==0 it means we already have a 'b' in our subsequence and when n==1 it means we do not have a 'b' in our subsequence then why we call the function as solve(0,0,0) that is by setting n to 0 . Or Am I wrong somewhere ? Please explain why we will begin by assuming that we have a 'b'. UPD 1: I have figured it out that if we will not assume b in beginning than all the a's before the first 'b' will be ignored and our problem will not be divided into subproblems.
It's because when we start a new subsequence we didn't need to have a 'b' before the first 'a'.
More formally 'n' represent whether we can start a new subsequence from the current index or not.
I made it bottom up this way: The state will be the current index, with the guide question: "how many ways to make valid sequences 'til here?".
the answer for dp[i], will be all the ways to dp[i-1], plus, if the current char is 'a', you can start one new sequence here (so, plus one), or extend all the previous valid sequences before the last 'b' (because you must have an 'b' between 'a's), which means that you can extend all the valid ways until the index of the last 'b', that turn out to be dp[index_of_last_b].
solution: https://codeforces.me/contest/1084/submission/46886918
Anyone please help me to find the fault in my 46870177 of 1084B - Квас и Орехус.
Guy, I read your code and your error is make the division integer, if you variables is unsigned long long all your operation with your variables will give a result with this type,backing to the problem when you user (int) will give error when the division gives a large result. My submission 46889415 of your code.
In Div2 D or Div1 A
Test Case :
3
5 24 24
1 2 16
1 3 14
Although, the answer would be correct by approach described above. But I am interested in calculating answer when the turning vertex is 1. By this approach it will be (8+10+5) where 8 will come from 24-16 and 10 will come from (24-14). But in actual that path is not at all possible. Because if we start from 2 and reach to 1 gas is = 13 but to go to 3 we need 14, cann't go to 3. same will be the situation when we start from 3 and want to reach to 2.
Could anyone explain me why this is not affecting final answer to problem?
If at any moment the sum becomes negative then the path is not optimal since you can remove the negative part, so even if you incorrectly consider it, the answer wont change since there will be a better solution anyways.
Thanks!!
But how can you guarantee that there will always be a better solution ?
Because removing the negative prefix leads you to a bigger sum
Why
⌊v−(s+n−1)/n⌋not⌊v − s/n⌋ + (s % n) ? 1 : 0?That are the same thing.
Can anyone explain in detail how to solve Div. 2 D?(I will be very grateful.)
Google Kadane's algorithm (for finding maximum sub-array sum) and then compare that technique here also. It helps me!
After struggling for some time on this problem, I finally have a proof of the algorithm that the author is proposing. Here it goes (along with the detailed explanation on how to solve the problem):
First, some terminology, that I'll use (I assume that we initially root our tree at the vertex 1): Let's define the sum on a path starting at a vertex u and ending at a vertex v as the sum of weights of all the vertices on the path minus the length of all the roads on the path, and the sum on a path starting at a vertex u and leading to a vertex v as the sum of weights of all the vertices on a path (excluding v) minus the length of all the roads on the path. Note: In this, I consider that v is always an ancestor of v.
We propose that the answer is simply the maximum of the (sum of the 2 longest paths leading to a vertex v + w[v]) over all the vertices in the tree. In case there are lesser than 2 such paths having a positive sum, we can take the other path(s) as having a sum of 0, they simply include no other vertex except v.
To elaborate more on the paragraph above, we can perform a dfs starting from the root node and since we know that there are only 2 possibilities: either the optimal path passes through the vertex v that we are currently at or it does not. I can compute the answer as the max. of the 2 possibilities. The thing proposed above is the max. sum of a path that passes through the vertex v, the other possibility can be considered by recursively computing the answer over all the children of the vertex v.
This is almost a standard kind of an approach that can be solved by a dfs. Here is my code for reference: 46893082 .
Now, onto the proof of this approach, mainly the thing about how can it guarantee that at no instant the fuel becomes negative. We prove this by contradiction.
Let us assume that our algorithm finds an optimal path in which the fuel becomes negative somewhere in the middle. Let's assume that the path goes from a vertex a to a vertex b and the answer was found at a vertex x. In this case, I can decompose the path (a -> b) as (a -> x -> b). Now, there are 2 cases:
1) The fuel becomes negative on some edge on the path (a -> x): Let's assume that the corresponding edge is from u to v. Now, consider that the total fuel at u was x and the edge weight is y. Now, in this case, the max. sum on the path that gives us our optimal answer is the max. sum on the path (u -> b) + (x - y), and (x - y) < 0. So, following the path from (u -> b) gives us a greater sum than the optimal path, which is a contradiction to our choice of optimal path, and since (x — y) < 0 , our algorithm would not consider this as the longest path ending at v, but it would rather consider some other path having a positive sum or simply the path starting off at this vertex whose sum is 0. This shows that the algorithm would never fall into such a situation.
2) The fuel becomes negative on some edge on the path (x -> b): Let's assume that the corresponding edge is from u to v. The same reasoning as above can be applied and we can get a better path (having a greater sum) than the optimal path by starting off at vertex v, and since our final answer is the maximum over all the vertices, it would rather consider that path as the answer as the optimal path. Again a situation that is not possible.
This shows that on the path chosen by our algorithm, we would never run out of a fuel. Further, our algorithm considers for all the vertices the optimal path passing through them and takes their maximum. Thus, our algorithm gives us the correct answer.
Hope it helps. :)
great! it helps a lot!
Nice post! Can you help me out in this? I have used the in-out dp approach to solve this problem. I don't know why it is failing on test case 34. https://codeforces.me/contest/1084/submission/46897634
I don't actually know what's the in-out dp approach that you are referring to. But anyways, I don't think any other person would understand your code better than you do. So I'd suggest you to find out the reason for why it fails on your own. You might end up learning a new thing from that.
Will you please go through my test case just 6-7 comments above. I think that don't come in both of these categories.
Consider case 2 of my proof. Here, x = 1 and b = 3. The algorithm at vertex 1 considers the optimal path to be of value 13 + 10 = 23. This is the only possible path. But on this path, the fuel becomes negative. This happens at the edge (u, v) where u = 1, v = 3. Now, in this case, it is optimal to start at the vertex v = 3, where the answer = 24. I agree that it's an invalid path and the algorithm considers it. But that's exactly what case 2 states, if this would have been a path that our algorithm considered as the answer, the fuel would have become negative on the edge 1 -> 3 and we would have been better off starting off at 3. But yes you're right. Here the algorithm at the vertex 1 chooses a path that is not possible. So, we can't say that the algorithm actually finds a valid path passing through every vertex, but we can guarantee that it finds an optimal path based on the reasoning given by the above 2 cases.
Ok got it. Thanks for going through my test case.
вот ты говоришь, что в div1a путь может быть как сумма двух дп, а дп — это лучший путь вниз из этой вершины;
но ведь может быть так, что вниз путь есть, а обратного пути вверх нет, так как может не хватить бензина там.Can someone please explain problem number D of Div. 2 ?
Look at my reply to the above comment.
Why these downvotes ? I just wanted to ensure that he gets a notification in case he doesn't look at this blog post again thinking that he got no reply.
Спасибо за раунд, задачи были очень интересными.
Thanks for your fast Editorials. <3
Prob div1E: Will a greedy solution work instead?
For each rectangle I define net exclusive area to be: "exclusive" area of each rectangle (which is area not shared by any other rectangle) — a[i].
The greedy solution is to find the rectangle with the lowest exclusive next area and delete it(only if the value is negative) and update the neighbor rectangle values and continue the process.
If we have 3 rects and lowest negative value at middle. There is can be situation when optimal solution is only middle. But your algo will exclude it. For instance: 3 3 7 1 4 3 4 1 3
If deleted rect will be always utmost than it will give correct solution.
"If deleted rect will be always utmost than it will give correct solution." Can you explain this?
On samples where you algo will always delete rect that is utmost among left ones, you will get correct answer. Otherwise result correctness is not guaranteed.
Why do the rectangles in problem E have to be non-overlapping for the solution to work?
They are overlapping, but not nested. If they were, finding area of intersection would not be as easy as xj·yi.
Actually most of solutions will work without any changes. Obviously, optimal answer will not contain nested rectangles, so we can't get worse answer. Also if we left the same formula for intersection, pair of nested rectangles will give less score, than it should give actually. So we will not get the answer, that is bigger than optimal.
Thanks, I hadn't thought of that. The only thing is that yi will no longer be in decreasing order. The nested rectangles can also be removed in linear time for convenience before doing dp, if I'm not wrong.
Oh, I doubt that they can be removed, because they have different ai.
The test for example:
I didn’t say to remove them, just keep the solution unchanged. My argument is that in the solution itself there shouldn’t be any nested rectangles, and the dp formula somehow compensates that by giving a negative score to having nested rectangles. Am I missing something?
EDIT: Never mind, I misinterpreted your last comment.
As I see only reason is that with this assumption simpler to build envelope.
Even as sad in editorial total time "O(n) if rectangles are already sorted".
Не давайте ему писать разборы
can anyone explain me this part in Problem C (DIV 2): For each i (1≤i≤k), spi= 'a'. For each i (1≤i<k), there is such j that pi<j<pi+1 and sj= 'b'.
We must create an array 'p' of indices that correspond to the letters 'a'. Between all adjacent elements of this array should be an index corresponding to 'b'
For Div1E I've wondered that my O(nlgn) solution get TLE for 2sec with n=1e6. Even after using vector instead map and releasing tie between cin and cout.
There is an easier way to solve problem Div2 E.
Let dp[i] represent the number of all distinct prefixes that end at i and are not less than S's prefix or larger than T's prefix, initially dp[0] is 1, and we treat strings as one based.
Initially, dp[i] = dp[i — 1] * 2, because you can expand all previous options by an 'a' or 'b'.
However, this recurrence counts prefixes larger than t and smaller than s, but the over counted strings can be at most 2, which happens if s[i] == 'b', or t[i] == 'a'. but in these cases you can remove them individually. (They can happen when you use S[1..i], and extend it by an 'a', or use T[1..i], and extended it by a 'b')
Once all prefixes are calculated, the answer is the sum of the dp array, but any dp[i] can't contribute larger than K prefixes ( since we need at most K distinct strings), so instead dp[i] contributes by min(dp[i],k)
This approach could also be extended if the question did not limit to using only 'a' and 'b' but had rather used the entire lowercase letters.
Solution: https://codeforces.me/contest/1084/submission/46911068
Thanks man! I loved this solution
so elegant !
helped a lot
In 1083E, shouldn't the formula be dpi =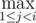 dpj + xi.yi - xj.yi - ai. Otherwise it will just give the area covered by all the rectangles.
dpj + xi.yi - xj.yi - ai. Otherwise it will just give the area covered by all the rectangles.
And what is the convex hull trick? Can someone explain/provide a link.
Never mind found it: Convex Hull Trick
Could someone explain what sequences do I need to count in Div2-C? Are they "aaa..." or" aaa...baaa..."?
Can anyone explain div 2E ? In the editorial, I understood till the part where problem is reduced to (k-2) strings and the common prefix of S and T are removed. But after that (from second paragraph), I can't understand much. I have understanding of both tries as well as binary tree. Can anyone help?
Each string is a path in trie. We want to choose k pathes between s and t and maximize c, which is equal to number of vertexes in union of them. For every "a" in string s and every "b" in string t we have complete binary tree in trie with some height.
In complete binary tree with height h we can consider multiset {h, h - 1, h - 2, h - 2, h - 3 (4 times), ...}. It can be proved that maximal union of l vertical ways in complete binary tree is sum of first l elements of this array, and if we want to choose some number of ways in two trees, we can combine their multisets. Let's store this huge set as array p, where pi is count of element h - i. For complete binary tree p looks like {1, 1, 2, 4, ...}. We can sum arrays to combine multisets.
It's not difficult to sum arrays for O(n) complete binary subtrees fast.
Could somebody help me find out my mistake in my solution?
It fails on the 14th test case
https://codeforces.me/contest/1084/submission/46908137
So basically i have three 1-D arrays up,down and cross. Initially i root the graph at node "1" to form a tree
up[i] holds the value for the maximum gasoline possible ending for an upwards path ending at i
down[i] holds the value for the maximum possible gasoline on a downwards path starting at i
cross[i] holds the value for maximum possible gasoline on a path with i as the turning vertex
Initially up[i]=down[i]=cross[i]=gasoline[i] for all i
up[i] is nothing but maximum over up[i] and up[j]-(distance between i and j)+gasoline[i] for some child j of i
similarly down[i] is maximum over down[i] and gasoline[i]-(distance between i and j)+down[j] for some child j of i
cross[i] is (for all pairs of children j and k): maximum over
1) cross[i]
2) (going from j->k)
up[j]-(distance between i and j)+gasoline[i]-(distance between i and k)+ down[k]
3) similarly go from k->j
What is wrong with my logic? :( I have read a solution below but i would also like to know what is wrong with my solution.I'll be very grateful if you could help me out cause i've been struggling for a while. Thanks in advance
Is the runtime for problem C missing a Qlog2N term? On each query swapping two values, each of the logN updates to the segment tree's nodes may involve an LCA lookup in logN.
You can do it in O(1) using Sparse-Table.
Didn't know about that, thanks!
Actually if you store middle node for non-vertical path too, you'll need to compute lca not more than once per query, because it happens only when you merge to vertical paths and in result you get a non-vertical one. So you can still compute lca with binary jumps.
Interesting. How can you perform the case where two vertical paths add to a vertical path in O(1) if you are doing LCA with binary jumps?
If two paths together form a vertical path too, you can say, that it’s endpoints are nodes with the maximum and the minimum depth. After that you just check that all other nodes lie on a path between them.
How can you check that the other nodes lie between them without doing LCA lookups?
It is enough to have
isParent(u, v)function, which uses only in and out times.Div 2 C: Can anyone explain what's wrong with my code? Maybe I divide on ‘a’ — bloks incorrectly? 46914444
Your mod constant is wrong. It's 1e9 + 7, not 10e9 + 7.
No, it is correct.
It's wrong mate. In C++, 1e9 === 1,000,000,000. You have used 10e9 == 10,000,000,000.
Whatever you say, boss. :P
Besides, you access beyond the vector's range — the condition 'ptr != n' in the two inner while loops should be the first.
Guys, what is needed to solve Div2 Problem D? I know DFS but I am not able to understand the approach to be used for this problem. For me, the editorial above is providing no clue/ help. Can someone help me with some explanation on this problem?
Thank you.
For a node i, dp[i] denote the answer when you start at node i and move down. you calculate dp[i] as d[leaf] = w[leaf] and dp[i] = max{dp[j] + w[i] - c(i, j) : j is direct child of i }. Consider a path which has maximum value, this path has a node N which is at minimum depth, either the path starts at this node and goes straight down or passes through N and divides into two paths both of which moves down. So to calculate the answer you take maximum of
dp[i] — path moves straight down or,
dp[j1] + dp[j2] + w[i] - c(i, j1) - c(i, j2) — path passes through node i and moves down to j1 and j2 with j1, j2 as direct child of i.
and update the answer. here is the code https://codeforces.me/contest/1084/submission/46876865
If I understood correctly the explanation for div-1 B, it will be better to change "Let's add the first 1 at the end." to "Let's add the first 1 in the end.".
So the idea is like this, let's name our array a which has length m, we have to add [1, 1, 2, 4, 8, ...] (length is H) to our arrays last H elements. To do this we forget about first 1 and add second 1 to am - H + 1. We do this for each group. Then start from element a0 and add 2 * ai to ai + 1. And finally add every 1, which we intentionally forgot, for each group, at the needed index.
Thanks, you are right. I'll fix it.
Does this Div. 1 F require many constant optimalizations? I came up with the intended solution but got TLE on test 10 or 11 plenty of times.
Try submitting your solution with GNU C++ compiler without diagnostics.
Got Accepted. Thanks!
In the solution of div2 B you wrote that if sum of all a[i] is <=s the answer is -1, but actually if sum==s the answer is 0.
Can somebody explain what is going on in problem : https://codeforces.me/problemset/problem/1084/B ?
What does least mean in
kvass level in the least keg is as much as possible.?we can get 1 liter of kavss from any not empty kegs, and each time we pour 1 liter from a keg, the level of it will decrease by 1. After we get s liters, the levels in some kegs will be decreased. So our task is to maximize the lowest level.
How to do the Div1 C question, the editorial is unclear to me. I am not able to understand how the queries to swap the values of the two nodes will work with the segment tree. Please help
|p−x|+|x−1|+|p−1|=2(max(p,x)-1) CAn somebody explain this ??.. I am a newbie
If we expand modules we will get this:
So we know from problem situation that it is always true.
When you get the formula
|p−x|+|x−1|+|p−1|, you know that x >= 1 && p >= 1, so then you will convert it to|p-x| + x + p - 2. Then just expand the module and you will get the final formula.I am is a beginner and i was solve to proble A, but i have a problem with this cide:
include <bits/stdc++.h>
using namespace std; int main() { int n; cin >> n; vector a(n); for (int i = 0; i < n; i++) cin >> a.at(i); vector sorted(n); copy(a.begin(), a.end(), sorted.begin()); sort(sorted.begin(), sorted.end()); int x; for (int i = 0; i <= n; i++) if (sorted.back() == a.at(i)) { x = i; break; } int onX, nX; for (int i = 0; i < n; i++) { if (a.at(i) == a.at(x)) onX += x * 4 * a.at(i); nX = (i — x) * 2; if (nX < 0) i *= -1; nX += i * 2; nX += x * 2; nX *= a.at(i); } int sum = onX + nX; cout << sum << endl; return 0; }
When i was compiling that code using my compiler that was has result 16 (correct). But when i submitting this code on pretest 1 that not has result 16 (that result is 28, and sometimes resulting random number) What's wrong??
You are using values of uninitialized variables
nvm
DIV 2 -> Problem D — The Fair Nut and the Best Path
Can anyone please explain the meaning of line in italics in this statement?
Nut wants to rent a car in the city u and go by a simple path to city v. He hasn't determined the path, so it's time to do it. Note that the chosen path consists of only one vertex.
Please read the original statement again. It says "the chosen path CAN consist of only one vertex". This means the answer can be the amount of gasoline that can be filled at a particular station.
Very kind of you to answer.
But the problem was solved.
Thanks anyways.
And an upvote too...
Happy Coding.