SPOILER ALERT : If you didn't solve the problems in NEERC and you want to enjoy the problems, please don't read.
It looks there are few problems about general graph matching in the community. And there are a few teams who solved problem B in NEERC both online and onsite. However, the reduction from maximum cost perfection matching to this problem is simple to me. So I want to share some problems for practice.
You can find the template here and here.
The shortest code of the maximum cost matching problem is about 5.7k.
There is a simple way to find the cardinality of the maximum matching, which is half of the rank of the Tutte matrix. We can use Gaussian elimination to compute the rank of a matrix. By the way, if the maximum cost is no more than W, we can also find the maximum cost matching by Tutte matrix and polynomial interpolation in O(Wn3). It is easier to implement.
Here is a collection of general graph matching problems. I'm too lazy to write solutions to these problems. And I can't remember the solution to some problems clearly. You can discuss the problems here.
Chinese postman problem. Find a shortest closed path or circuit that visits every edge of a (connected) undirected graph.
Given an undirected weighted graph G, find a minimum weight subset E such that each vertex is incident on at least one edges in E.
Min cost cycle cover. A cycle cover of an undirected graph is a collection of vertex-disjoint cycles such that each vertex belongs to exactly one cycle. We require each cycle contains at least three vertices. In a weighted graph, the weight of a cycle cover is the sum of the weights of all its edges. Find the minimum total weight cycle cover.
Given an undirected positive weighted graph G, find the shortest simple path from s to t with even edges.
A problem from winter camp 2016 There are n balls and m baskets. There are e relationships such that ball u can be put into basket v. We can put at most 3 balls in each basket. And we want to put every ball into baskets. We want to maximize the number of baskets with at most 1 ball.
A problem from Chinese Team Test 2013 Find the maximum cut of an undirected planar graph. You need to partition the vertices into two sets S, T. Maximize
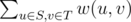 .
.Two matching. Given an undirected weighted graph G, find a minimum weight subset E such that the degree of each vertex in the subset E is no more than 2.
Undirected Vertex Geography. Alice and Bob are playing a game on an undirected graph. They move the token to the unvisited neighbor alternatively. The player who can't move loses. Determine the winner of each starting point. Algebra makes your life much easier in this problem.
Given a DAG. You can remove at most 2 vertices with zero in degree in each round. How many rounds do you need to remove all the vertices?










Auto comment: topic has been updated by jqdai0815 (previous revision, new revision, compare).
"about 5.7k" to you means that every self-respectful person must be able to memorize it?
You know that FFT is still considered to be quite hard algo, despite being 15 lines long?
I just want to discuss the possibility of implementing(copying) this algorithm in an ICPC contest.
No problem setter should want you to implement this in official contest where you can't copy-paste.
Problem B from last NEERC is a bad example of a hard problem for an official competition. Problem H is much better — harder to solve but relatively easier to implement.
The intended solutuon is maximum cardinality matching. I think this algorithm should be included in the team code library, and it is not too long (~1k). I think this problem is ok in an ICPC contest.
I agree with Coder. I don't like problems that require the knowledge of too advanced algorithms. Then the contests will be like "who learned the biggest amount of advanced algorithms?" and it will be just like studying. Problems that can be solved by a combination of simple algorithms and your own idea are much nicer.
I don't agree on you. I think Blossom is not that advanced in the algorithmic literature, and it's not hard in implementation. Compare this to discrete k-th root (It's Adelman blah blah, I saw it in some GP but forgot) or fast linear recurrence solver. Blossom is just a textbook algorithm.
However, your point is also valid, contests only asking for advanced algorithm is also bad. NEERC 2018 was balanced in that point, as it featured both problems.
Also, considering that ICPC WF even features physics problem, I think your wish is very unlikely to be realized, regardless if it's right or not..?
I would like to add that in that NEERC problem there was no need to write complicated (I don't think I am able to code it fast without team notebook) blossom algorithm. You don't need a certificate, so you just need to compute rank of Tutte matrix. Gauss algorithm is much easier I think.
Regarding blossom/Adleman I have exactly opposite view :P. Baby step giant step is pretty short and intuitive and Adleman was not about knowing it before but about coming up with it knowing BSGS. And I consider blossom as something really painful.
Our teamnote have a neat implementation by Konijntje. He explained this in his blog, unfortunately in Korean :(
The point is, whenever you have to "contract" the blossom, you don't really need that, but rather expand the blossom into two. Then, you don't need to explicitly mutate the structure, just storing blossom indices are OK. This is not addressed in wikipedia, and this trick makes implementation very easier.
Nice, that's pretty short. The problem with blossom is that it's so rare and so few people know it, but I can see it becoming more widespread once people find out there is an easy implementation.
Also, I noticed the weighted version is 3x as long as the unweighted one...
IMHO, the only difficult part of fast linear reccurence solving is taking a polynomial modulo another in . And it is often unnecessary (because O(n2) is good enough) or can be avoided by exploiting special structure of the characteristic polynomial in most problems involving fast reccurence solving I encountered.
. And it is often unnecessary (because O(n2) is good enough) or can be avoided by exploiting special structure of the characteristic polynomial in most problems involving fast reccurence solving I encountered.
Moreover, the idea behind the algorithm is quite intuitive and arises directly from solving the linear recurrence in the most straightforward way: say you have recurrence an + 2 = 2an + 1 + 3an. Its characteristic polynomial is x2 - 2x - 3. Then a4 = 2a3 + 3a2 = 2(2a2 + 3a1) + 3a2 = 7a2 + 6a1 = 7(2a1 + 3a0) + 6a1 = 20a1 + 21a0. Similarly,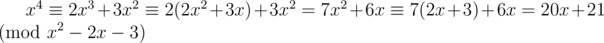 .
.
The transformations happenning are not just similar, they are exactly the same!
I don't think that it is more complicated than matrix multiplication from the theoretical standpoint. From practical standpoint, there are some troubles if naive polynomial multiplication and division are not fast enough for the problem — but in this case matrix multiplication won't work as well.
The "polynomial modulo" was exactly what I wanted to address. I agree is neat.
is neat.
In my opinion, problems requiring heavy library algorithms (especially those that are really rarely used in most contests) are bad in official competitions, but problem B from NEERC is an exception:
1) There were plenty of problems to solve, most of which required only some well-known algorithms like DFS. 9 problems were enough to get into gold medals.
2) It was easy to see that this problem requires some non-standard algorithm — one could prove that maximum matching problem in arbitrary graph can be reduced to this.
3) The problem was not straightforward. Knowing maximum matching algorithm and being able to code it was not sufficient to solving it.
4) The constraints were low and it was not required to restore the answer, so we could apply some techniques like Tutte matrix or even randomized Kuhn (I'm not sure actually whether it can get AC, but nevertheless) to solve the problem.
And now compare it to problem G from World Finals 2018, which, in my opinion, is an example of a bad ''library'' problem.
Any problem with 0 accepted is bad by any definition no matter how many other problems were there and how you try to justify it
Do you really think so? Is problem D from NEERC also a bad problem?
I made a mistake trying to discuss something seriously, will go back to trolling as usual
What does 5.7k mean in this context? 5.7k lines? 5.7k characters?
FFT in 15 lines? wow. Can you please provide a link to the implementation?
38799873
FFT is 14 non-empty lines, but you also need initFFT, which is 7 non-empty lines. I guess that my implementation is not shortest.
The following is a modest update to your FFT function implemented in 9 non-empty lines. The initFFT function is implemented in two C++ data structure constructors, and functions dealing with long long integer vectors are wrapped up in one data structure.
46649368
What the fuck is wrong with you
Nothing should be wrong in revising some appreciated code and sharing the update with its author.
spaces in brackets LUL LMAO ROFL
There is nothing too funny with spaces in brackets to make some code more reader friendly, in my humble opinion.
more friendly (unreadable)
The following is almost the same code except for using abbreviated names, restoring the initFFT function and leaving no spaces before and after the parentheses, brackets, and operators. This is definitely less funny and more serious code that may save few precious seconds in typing space characters and long identifier names during competitive programming contest. However, this is not the same situation when someone is only practicing or revising some code. Finally, the choice is yours as to which revision is more reader friendly.
46657091
Very interesting exercises. Thank you!
I believe we should calculate s — t cut, not global, in problem 6. Am I right?
A more detailed description is added.
Ooh, it was not :(
Seriously, how tf is that possible to find a maxcut in planar graph xD? I would have never thought it can be polynomially solvable
The set of edges in a cut is bipartite. Let's look at the faces of our graph: they form cycle basis, so the graph is bipartite iff they all have even length. In dual graph it means we have to choose maximum weight subset of edges so that all degrees are even. This is equivalent to problem 1.
The problems are very interesting! Now I kind of want to learn Edmonds algorithm.
OK, let's crowdsource solutions to these problems:
We need to assign each edge positive multplicity so that for every vertex sum of multiplicites of edges incident to it is even. Then we can find this circuit by finding Euler's cycle. We think of it as firstly putting multiplicities 1 and adding something to fulfill this condition. We create a new weighted graph on vertices with odd degree where we have edge between every pair of vertices and their weights are corresponding distances in original graph and we take min full matching in this new graph. Every edge corresponds to some path where we put multiplicities 2 instead of 1.
Maxcut == m — minimum number of edges needed to be deleted to make it bipartite. Planar graph is bipartite iff all its faces are of even length. We take dual graph and we look at odd faces and we create a very similar graph to that one from postman problem. We make a weighted clique on odd faces where weight of an edge is distance in dual graph. Such edge corresponds to deleting edges in original graph corresponding edges in dual graph connecting these two faces.
Stupid putting spoilers deleted my elaborate solution with proof, so I'm gonna keep this short. Put an edge iff two vertices are incomparable and answer is n — max matching.
You can find problem 8 in this pdf.
Problem 8 is in Codechef, and our ICPC team used it to check our blossom implementation.
The problem is well-known (CERC 2011 R and many more). It's really beautiful, and one of my favorite problem. However the proof is very simple, so I don't know how algebra helps here.
It's well known in Poland (it was known even before CERC 2011 where some people already knew it) and I have to admit it's one of my favorites problems as well :)
First, you can easily reduce this problem from checking if every edge is in the perfect matching by adding dummy vertices.
It can be solved by Rabin Vazirani lemma: If G has a perfect matching, and A is the Tutte matrix of G, G - {vi, vj} has a perfect matching iff (A - 1)i, j ≠ 0.
So it becomes a pure linear algebra problem. I'm more willing to find the inverse matrix than finding an augmenting path in a blossom graph xD
Let's color edges on a path in black and white alternatingly. Then black edges form a matching covering all vertices on a path except s and white edges form a matching covering all vertices except t. Let's build 2 copies of our graph, G0 and G1 for black and white matching respectively. For each v ≠ s, t v is either in both matchings or in neither. To achieve it, let's add edge v0 - v1 with zero cost. s should not be in black matching, so let's add new vertex s2 and edge s0 - s2. s should be in white matching, so no new edges for s1 needed. For t by similar logic we should add vertex t2 and edge t1 - t2. Min cost perfect matching in this graph corresponds to shortest path with even number of edges. By the way, if we add edge t0 - t2 instead t1 - t2 we will find shortest path with odd number of edges. Also this solution doesn't work with negative edges, any ideas on how to fix it?
Sorry, the edges should be non-negative here. The problem should be as hard as Hamilton cycle if edges can be negative.
First, take all negative edges. Let's delete all vertices covered by them. If there was an edge connecting uncovered and covered vertex, let's say that now it connects uncovered vertex to itself. Now all edges are nonnegative.
Let's look at the answer. If there is a path of length at least 3 then we can delete the middle edge on this path and our answer will improve. It means in optimat answer each connected component is a star(possibly with a single edge). For each star let's choose one edge in it. Then chosen edges form a matching. For all vertices not in this matching it's optimal to choose the shortest edge incident to that vertex. Let's build 2 copies of the graph and for each vertex v connect v0 and v1 with an edge with weight equal to the shortest edge incident to v multiplied by 2. Then the answer is min weight matching divided by 2.
For each edge v - u let's create separate copies of vertices v and u. For each vertex v our matching should contain exactly 2 edges incident to v. Let's create deg(v) - 2 additional vertices and connect them to all copies of v we created with 0 weight edges. Now perfect matching will match those deg(v) - 2 vertices to deg(v) - 2 copies of v and other 2 copies will correspond to edges in cycle cover.
It seems that an edge will be chosen twice in the matching.
No. Each edge has 2 vertices corresponding to it. It is taken iff the edge between those vertices is taken. Otherwise, both of those vertices are matched with one of additional deg(v) - 2 vertices. How could we take the same edge twice?
Let's prove that the answer from the above post is correct. It suffices to show that given a matching $$$M$$$ where each matched pair in $$$M$$$ is incomparable, we can remove all vertices in $$$n-|M|$$$ rounds.
Specifically, we will describe how to remove vertices and modify $$$M$$$ such that $$$n-|M|$$$ decreases by exactly one during the first round. Let $$$S_0$$$ be the set of all vertices with in-degree 0.
Case 1: $$$S_0$$$ contains a vertex not in $$$M$$$.
Remove any such vertex in the first round.
Case 2: $$$S_0$$$ contains a pair of vertices matched in $$$M$$$.
Remove any such matched pair in the first round.
Case 3: All vertices in $$$S_0$$$ are matched, but $$$S_0$$$ does not contain a matched pair.
Given $$$v\in S_0$$$, let $$$m(v)$$$ denote the vertex matched with $$$v$$$ in $$$M$$$ (note that $$$m(v)\not\in S_0$$$).
Lemma: There exist $$$a,b\in S_0$$$ such that $$$m(a)$$$ and $$$m(b)$$$ are incomparable.
If the lemma holds, then we can remove $$$(a,m(a)), (b,m(b))$$$ from $$$M$$$ and insert $$$(a,b), (m(a),m(b))$$$ into $$$M$$$, reducing to case 2. It remains to prove the lemma.
Proof of lemma: Let $$$x\leadsto y$$$ mean that there is a directed path from $$$x$$$ to $$$y$$$ in the original DAG; then $$$x$$$ and $$$y$$$ are incomparable if $$$x\not\leadsto y$$$ and $$$y\not\leadsto x$$$. Now let's construct a new directed graph $$$D$$$ on $$$S_0$$$ where $$$x\to y$$$ in $$$D$$$ if $$$y\leadsto m(x)$$$. Since every vertex in $$$D$$$ has out-degree at least 1 and $$$D$$$ has no self-loops, $$$D$$$ must have a directed cycle $$$v_0\to v_1 \to \dots v_{k-1}\to v_0$$$ with $$$k>1$$$ and all $$$v_i$$$ distinct. Since $$$v_{(i+1)\pmod k}\leadsto m(v_i)$$$ and $$$v_{(i+1)\pmod k}\not \leadsto m(v_{(i+1)\pmod k})$$$, we must have $$$m(v_i)\not\leadsto m(v_{(i+1)\pmod k})$$$ for all $$$i$$$. Also, there must exist some $$$j$$$ such that $$$m(v_{(j+1)\pmod k})\not\leadsto m(v_j)$$$, or the original DAG would contain a cycle. Then $$$m(v_j)$$$ and $$$m(v_{(j+1)\pmod k})$$$ are incomparable, so the lemma is proven.
What are some good sources on implementing general matching? Both maximum cardinality and maximum weight versions. I can find some versions (e.g. here) but I'm not sure if it is feasible to fit them into a codebook. Is there something reasonable running in o(n3)? Or does one usually just compute the rank of the Tutte matrix? Thanks!
versions (e.g. here) but I'm not sure if it is feasible to fit them into a codebook. Is there something reasonable running in o(n3)? Or does one usually just compute the rank of the Tutte matrix? Thanks!
This is an algebraic approach to maximum cardinality matching with a certificate.
The algebraic approach is slow, but it's easy to implement and remember.
When it comes to finding a maximum matching instead of the cardinality, it becomes much more complicated. I think the combinatorial one is better.
There are also some randomized (heuristic) and super short approaches here to find the maximum cardinality matching, and we don't know how to fail them now.
http://acm.timus.ru/problem.aspx?space=1&num=1099
This problem asks you to find max. cardinality matching in a general graph and print edges.
Randomized solution gets WA 12 while both blossom and algebraic solutions get AC.
Submissions for randomized and algebraic ones.
According do Burunduk1 there are graphs where the probability for randomized algorithm to find max. cardinality matching is exponentially small.
I read his claim here, unfortunatelly in Russian. He doesn't specify what type of graph it is.
http://acm.math.spbu.ru/~sk1/courses/1718f_au2/conspect/conspect.pdf
I increased the randomized time from 5 to 500 and it got accepted now.
Actually, the problem puzzled me several years that if there are hard cases under the constraint we can accept in the algorithm contest (like n ≤ 1000).
There is an implementation of the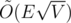 algorithm by Min_25 on github. It's long, so not really suitable for ACM codebooks.
algorithm by Min_25 on github. It's long, so not really suitable for ACM codebooks.
There's also a long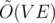 code for weighted general perfect matching by Min_25 on github.
code for weighted general perfect matching by Min_25 on github.
So many red coders discussing on this topic meaning this is probably way too difficult for me to understand. I was wondering it would be nice if the blogger put a rating on the blog. If it is above 2400 then I will probably ignore it.
NAC 2021 Problem H can be solved with a technique from exercise 4. Interestingly it is not an intended solution.
If we assume that the special edges are the perfect matching of the graph, the problem is equivalent of determining unique matching. (More specifically, it asks for a "counterexample" if the graph does not have a unique perfect matching.) Unique perfect matching can be determined by calling the maximum matching algorithm $$$O(N)$$$ times, but there is a well-known characterization that the 2-connected graph can't have a unique matching. I think this illustrates the difference between my solution and the official solution.