Editorials came in so early :)

Thank you Jeel_Vaishnav and Ashishgup.

Good contest,expect for the order of E and F.

Did anyone solve problem E with LP solvers? If yes, what's the solver needed? I am using simplex and it gives TLE :/

I love how there are Java and C++ code!

Is there any proof for the author's solution of D?

In F, final part may be a little bit easier. The root node is the node separated from any of two leafs by exactly h - 1 nodes (among the found 2h - 1 nodes). Still O(H²) though.

In the final part of F, you can use std::sort like this:

std::sort(path.begin(), path.end(), 
  [&](int u, int v) {
    if (u == v) return false; 
    return Query(leftmost, u, v);
  }
);

This decreases the complexity of fixing the order to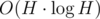 . Moreover selection algorithm will make it O(H).

Auto comment: topic has been updated by Jeel_Vaishnav (previous revision, new revision, compare).

What the F ;)

My solution of F -
Take any 2 random nodes, say u and v. The probability that root lies in the path of u and v is 1/2.

Perform query(u, i, v), query(u, v, i) and query(i, u, v) for all i.
if query(u, i, v) = Yes, then i lies in the path of u and v
if query(u, v, i) = Yes, then i lies in the subtree of v
if query(i, u, v) = Yes, then i lies in the subtree of u

We can find subtree sizes of u and v, and thus we'll get the level of u and v. We already know the level of the root. So, by checking the number of nodes in the path of u and v, we'll get to know whether root lies in the path or not.

If root lies in the path, then we can find the order of the nodes which are in the path (as mentioned in the editorial), and thus find the root.

Ashishgup can you plz provide explanation of your code for problem multiplicity.

Problem — Views Matter What will be the output for Input ?

3 3
3 1 1

shouldn't the output should be " 2 " instead of " 1 " Since " 3 " blocks can manage top and right view.

Illustration

*
*
* * *

Top View — 3
Right View — 3 After Changes

*
  *
    *

Top View — 3
Right View — 3 Help me, is this correct or did I misunderstood something. Task number — 5

Excuse me, could someone please show me what I have done wrong with the WA solutions ?

Correct sol : https://codeforces.me/contest/1061/submission/46112942

WA sol : https://codeforces.me/contest/1061/submission/46097011

Summarization: In both sol, what I am trying to do is too keep the all the ends of renting time of TVs, and for the current shows, I will decide to attach it to a TV or assign it to a new one, optimally. The only difference in two solutions is the sorting of the [li, ri]. In the WA, the array was sorted in accordance to ri, while in the correct one it was sorted according to li

wa in testcase 43 of problem D

https://codeforces.me/contest/1061/submission/46100789

What is wrong with the solution?

dp[i][j]={ dp[i−1][j]+dp[i−1][j−1] if a[i] is a multiple of j dp[i−1][j] otherwise } Can anyone explain me this equation.

I have another approach for F.

First case : k < 18

Starting from a random node (let's call it X), I basically find all of its k children and parent (if it's not the root). To do this, just find another random node which hasn't been marked yet (marking process is written below) and ask for the next node which lies on the path from our current node to it.

After finding one of its neighbor (lets call it Y), I mark all the nodes Z that ask(X, Y, Z) = "Yes", cause they are negligible.

You can easily notice that the parent of the current node is the vertice with the biggest number of vertice Z that satisfied the condition above.

If a vertice have exactly k neighbors, it's the root of the tree.

So there will be at most log(n) * n * 2 * k questions need to be asked in this case

Second case : k > 17

One thing to notice is that in this case, the depth of the tree is at most 3.

Now the idea is from a random node, find the longest simple path starting from this node and you will know exactly which node is the root on this path.

For instance, let n = 421 and k = 20 and you've found the longest path starting from node X which its length is 3 then you can be sure that the second node lying on this path is the root of the tree (sorry for poor explanation).

Now, to find the longest path starting from a node X, my solution is to get 50 other random vertices and find ask for the length from X to these nodes. One can easily see that the probability of getting one of the longest paths in this way is >= 0.5 for each random node we ask.

After getting nodes from one of the longest paths, you can easily sort this path in the correct order and find the answer.

Is there any way to test problem F on my machine?

I thought that the checker for F could be adversarial. Like if your algorithm is to randomly pick nodes until you get leafs where the root is their Lowest Common Ancestor, then the adversarial checker would give you neighboring nodes instead. It could defer assigning final positions to the nodes unless query answers lead to contradictions.

I think I have a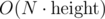 algorithm that does something like  ≈ 50N queries when the checker is as adversarial as possible and the tree height is 10 (which is the max for the problem).

I start with picking two random nodes a, b and making queries (a, x, b) until I find a node in between. That's N - 2 steps. Then I find the depth of x and all nodes reachable through it's parent by fixing a, x and making queries (a, x, y) and then fixing b, x and making all queries (b, x, y). After 2N - 4 queries you know which ones of a, b are above x, the depth of x, and all nodes reachable through x:s parent. If x is the root, we will detect it, because we know it's depth.

Then the idea is to find a node z on the path from x to the root, and continue going up from z. We pick any node t in the subtree reachable from x through it's parent. Then we check what nodes are on the path between x and t in  ≤ N - 2 steps. We also check the depth of t in  ≤ 2N - 4 steps. Then we sort the path from x to t to find the highest node on it. Sorting can be quadratic, but that's fine, because the path is  ≤ 19 elements long, and the longer it is, the higher up in the tree we will get.

Are the complexities for E correct? Min-Cost-Max-Flow should take O(nm) iterations (like Edmonds-Karp), and in each iteration Bellman-Ford takes O(nm), which gives O(n^2m2). In our case, since m = O(n) we would get O(n⁴).

I would appreciate if someone could help me understand why this submission 46126706 fails and this one gets AC 46126678. The only difference between them is in function f :(.

ll f(ll l, ll r){
	return (y * (r - l))%mod;
}

ll f(ll l, ll r){
	return (y * (r - l));
}

In problems like D, I always sort them by their ending time and all of them passed. Now It fails in test 43. Learned a new thing. Thanks.

Another similar approach for problem F: Get two random vertex (u, v). The probability that these are two leaf from distincts subtrees of the root is 1 / 8, so the probability of fail is 7 / 8 and after 40 random pick of (u, v) the probability of fail is around 0.004. For each pick ask for all the nodes that are in the path from u to v, if these number is exactly 2 * (depth - 1) - 1 then these are two leaf from distincts subtrees and the root is there. Only left check what of these nodes are the root, this can be done with n query, because for a fixed vertex and all the others the root is the only node that are in exactly in n - 1 - (n - 1) / k paths. 46130299

Pretty and short sweepline + greedy approach for problem D: 46130297

I am wondering whether problem C can get accepted submission using python ..

EDIT: I can get accepted using PyPy. Does anyone know whether there is some explanation regarding python submission for contest?

Here is my submission for C: 46183737. I get TLE, probably because my loops to calculate the divisors for every number is too slow. Is there something simple I can fix, or is my method just too slow?

Also, the author has a much more complicated way of calculating divisors. Is his way fast enough to use for pretty much every problem where it is beneficial to precalculate the divisors of numbers?

As per the editorial of F, all the 60n queries are exhausted in Part 2 and 3 only. How do we afford the additional queries for the Finally part? Please let me know what am I missing here.

upd
it was mistake in my idea
sorry for the trouble

In Problem C how can we find all the divisors of a number . Isn't it hard to construct all divisors by having only prime divisors ?

in order to find a leaf, we can act like this:

int find_leaf()
{
    u=rand(),v=rand()
    for i=1 to n 
        if query(u,v,i) 
            v=i; 
    return v; 
} 

then we can get a leaf in O(n),use n querys only.

Can someone please check my solution for C. Multiplicity It fails at tc no. 17 https://codeforces.me/contest/1061/submission/100703688

A solution with better probability of passing for Problem F than the editorial:

The main difference is that I can find any leaf deterministically. Pick two arbitrary nodes $$$D$$$ and $$$E$$$, set $$$a=D$$$ and $$$c=E$$$ then I can find a leaf node such that $$$E$$$ lies in the shortest path from $$$D$$$ to that leaf.

To do that: loop from $$$1$$$ to $$$n$$$, and whenever we find $$$j$$$ such that $$$query(a, j, c)$$$ is $$$TRUE$$$, then we update $$$c$$$ to $$$j$$$. Easy to prove, that this always finds a leaf of the desired property.

Now find any leaf $$$L_{1}$$$

Now, we just take $$$20$$$ random nodes, probability that at least one of them lies in a different subtree from $$$L_{1}$$$ is $$$1/2^{20}$$$. So we find a leaf from each of these nodes. Then check if they are $$$2h-1$$$ apart as in the editorial.

I like how they convert 2D to 1D in Prob C. learnt something new