Palindromic Query - Codeforces

6 лет назад, # |

← Rev. 2 →

Mistake in approach.

→ Ответить

6 лет назад, # ^ |

Thanks for your reply.

But I am not clear about the merging procedure. Can you please tell me more about this part "number of palindromes between this parts (left end in first half and right in second)."

→ Ответить

6 лет назад, # ^ |

← Rev. 2 →

why even O((r - l) * logn)? You can preprocess string using Manachar's algorithm, and then for each i in [l, r], you can find the number of palindromes in between the parts, centered at i in O(1), so it's just O(r - l).

but I don't understand, how it will be O(nlog²n) in total, because you will have to merge even for queries. Can you please elaborate.

→ Ответить

6 лет назад, # ^ |

← Rev. 2 →

[deleted]

→ Ответить

6 лет назад, # ^ |

We know that there can be at most n palindromes in a string of size n

No there can be n² palindromes, for example consider aaaaaa.

so that won't work :|

→ Ответить

6 лет назад, # ^ |

Sorry, you are right.

→ Ответить

6 лет назад, # ^ |

← Rev. 3 →

Mistake in approach.

→ Ответить

6 лет назад, # ^ |

"each interval will be smaller in at most logn merges"

No, you may even have to merge already merged intervals, with a simple interval. So that won't be O(nlogn)

→ Ответить

6 лет назад, # ^ |

You are absolutely right! I will try to invent something better and correct :)

→ Ответить

6 лет назад, # |

← Rev. 2 →

Sqrt-decomposition solution is costly but may pass, depending on TL.

Whenever you add/remove some index, you have to add/remove palindromic substrings ending at that index, which you can find using binary search (hash the string and it's reverse).

Total complexity will be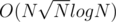 $\text{[math]}$

→ Ответить

6 лет назад, # ^ |

How will you find palindromic substrings ending at some index by binary search?

→ Ответить

6 лет назад, # ^ |

Hashing

Hash the given string and it's reverse, Now you can binary search on the maximum length that can be a palindrome ending at that index (in the direction you want). To check if the substring of given length is palindrome, you just compare hash of string with it's reverse, for that substring.

→ Ответить

6 лет назад, # ^ |

← Rev. 2 →

That is not correct, you can do it for center of string, otherwise function is not monotonic and you can not use binary search:

Just look at string aba, there is two palindromes and binary search will check first ba and say, ok it is not palindrome answer is smaller than 2.

→ Ответить

6 лет назад, # ^ |

oh ok.. missed it :(

→ Ответить

6 лет назад, # ^ |

1:1 in hacks, we are playing until 2 ;)

→ Ответить

Noam527

6 лет назад, # |

+20

It is easier to explain by considering only palindromes centered at indicies (so, odd length), the idea is the same anyway. For each index i, r_i will be the longest radius of a palindrome centered there (in other words, the amount of palindromes centered at index i). Directly from manacher, this takes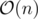 $\text{[math]}$ to calculate.

For a query [l, r], we first compute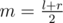 $\text{[math]}$ . Now we want to calculate

$\text{[math]}$

Again, thanks to symmetry, I'll only explain how to compute the left term.

$\text{[math]}$ .

The sum over i can be found in constant time. As for the other term, if we create some array r_i' = r_i - i during the preprocessing, then the queries are asking for some over range of min(C, r_i') where C is constant. You can solve this in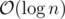 $\text{[math]}$ per query using wavelet tree, and I guess it's also solvable with a persistent segtree.

→ Ответить

6 лет назад, # ^ |

← Rev. 2 →

Thanks for your reply. This is an interesting approach.

Well, I am interested to know about this idea- min(i-l+1,r[i])=i+min(1-l,r[i]-i).

I have brute forced for different i,l and r[i] and found that this is true. But curious mind wants to know the proof of this. If you can come up with a proof feel free to share this with me.

Thanks again.

→ Ответить

6 лет назад, # ^ |

min(i - l + 1, r_i) = min(i + (1 - l), i + (r_i - i)) = i + min(1 - l, r_i - i)

→ Ответить

Noam527

6 лет назад, # ^ |

min(x + a, y + a) = a + min(x, y). I think this is fairly obvious, but you can do case analysis anyway:

x < y: min(x + a, y + a) = x + a = a + min(x, y).
x ≥ y: min(x + a, y + a) = y + a = a + min(x, y).

Now just plug a = i, x = 1 - l, y = r_i - i

→ Ответить