Sums and Expected Value — part 1

#	User	Rating
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

#	User	Contrib.
1	cry	167
2	Um_nik	163
3	maomao90	162
3	atcoder_official	162
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	Dominater069	153
9	nor	153

part 2: https://codeforces.me/blog/entry/62792

Watch my lecture-stream tomorrow (Thursday) at 14:00 CEST — ~~https://www.youtube.com/watch?v=qdlPY37MBPo~~ https://www.youtube.com/watch?v=U_h3IjreRek. I will go through theory and problems from this blog. The only prerequisite is knowing what is probability. The next (harder) part on Monday.

The video will be available later, with timestamps for each problem — so you don't have to watch everything.

Definition of EV

Let's say we bought a lottery ticket for 2$. We will win 10$ with probability 10%, and 20$ with p-bility 2%. On average, it gives us 0.1·10 + 0.02·20 = 1.4, so we are worse off after buying the ticket. The computed average is called the expected value.

The expected value (EV, expectation) is the average value of an event/experiment. For example, EV of the number of pips rolled on a 6-sided die is 3.5:

$\text{[math]}$

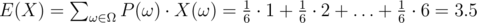
Linearity of EV (super important theorem):

E(X + Y) = E(X) + E(Y)

Technique "Contribution to the sum"

If we want to find the sum over many ways/possibilities, we should consider every element (maybe a number, or a pair or an edge) and count how many times it will be added to the answer.

EV easy problems

Aces We choose 10 cards at random from a standard deck of 52 cards. Find EV of the number of aces.
Inflation The price of a tv is 1000$. Each of the next N days, the prices goes up by 5$ or 10$ (each with p-bility 50%). Find EV of the final price.
Bonus: What if it goes up by 1% or 2% each day?
Max of two You roll a 6-sided die twice. Find EV of the bigger of two scores.
Max of N You roll a 6-sided die N times. Find EV of the biggest score.
A few possible solutions.
Birthdays You teach informatics in a class with 20 students. When someone has a birthday, you must let the whole class to play games instead of learning algorithms and using Excel. Maybe some students have birthday on the same day, so there would be fewer than 20 wasted days during a year? Find EV of the number of days when at least one student has birthday.
Bonus/fact: Birthday paradox.
First heads Find EV of the number of coin tosses until you get heads.
How to check your answer with a program?
Two heads Find EV of the number of coin tosses until you get heads two times in total.
Two heads in a row Find EV of the number of coin tosses until you get heads two times in a row.
Volleyball 12 teams, including Poland, play in the volleyball tournament. Teams are divided into 4 groups, each with 3 teams. In each group, every team plays against every other team, and then two best teams advance to the elimination stage. In case of a perfect tie, two random teams advance. The elimination stage has quarterfinals, semifinals and the final match. In every match, a random of two teams wins (50% each).
Find p-bility that Poland will win the whole tournament. Find EV of the number of matches won by Poland. Find EV of the number of matches won by Poland, assuming that they won the whole tournament (in other words, find EV of the number of matches won by the winner of the whole tournament).

Problems for "contribution" technique

Hills Given a sequence of length N (N ≤ 10⁵), count triples of indices i < j < k that a_i < a_j > a_k.
Bonus: Count zig-zags of length 10, i.e. i₁ < i₂ < ... < i₁₀ that a[i₁] < a[i₂] > a[i₃] < a[i₄] > ... < a[i₁₀].
Paths in tree Given a tree of length N (N ≤ 10⁵), find the sum of lengths of all paths. (Solve this without not-trivial dp or centroids.)
Bonus: Find the sum over squares of lengths of paths.
Sum over subsets There are N competitions, the i-th with prize a_i. You're quite good and you will win each competition with p-bility 50%. Find EV of the total won prizes.
Equivalently: Find the sum over total prize over all 2^N possibilities, and print answer modulo 10⁹ + 7. (This answer divided by 2^N gives the answer from the first version.).
Math encoder (Code Jam Kickstart 2017 round B) You are given a sequence of N numbers (N ≤ 2000 or N ≤ 10⁵). We're to choose one of 2^N - 1 non-empty subsets, uniformly at random. Find EV of the difference between the maximum and minimum element in the subset.
Equivalently: Find the sum over the difference over all subsets, and print the answer modulo 10⁹ + 7.
Imbalanced array (CF Educational Round 23) Same as the previous problem, but choose a random of N·(N + 1) / 2 intervals.
Bonus: Do it in O(N) if the input contains a permutation of numbers 1 through N.
Randomizer (CF 313 D) You're given a convex polygon with N vertices (N ≤ 2000 or N ≤ 10⁵). We choose a random subset of vertices, what gives us a new (small) convex polygon. Find EV of the perimeter of the new polygon.
Well, the CF problem was a bit harder, with computing area and using Pick's theorem.
Random CH You're given N points (N ≤ 200 or N ≤ 2000), no three are collinear. Each point disappears with p-bility 50%. Find EV of the size of the convex hull of remaining points.
(The size of CH is the number of its vertices.).
Eating ends You're given a sequence of length N (N ≤ 2000 or N ≤ 10⁵). N - 1 times we will remove the first or the last element, each with p-bility 50%. Find EV of the last remaining number.
Well, the implementation is hard because of precision issues.
Sum-length Given a sequence of length N (N ≤ 10⁵), find the sum over sum·len³ over all intervals. Print the answer modulo 10⁹ + 7.
There are a few possible solutions, including one that we will discuss in the next part.

#include <bits/stdc++.h> using namespace std; int n; // O(N^2) double solve1(vector<double> &arr){ double ans = 0; n = arr.size(); for(int i=0;i<n;i++){ for(int j =i+1;j<n;j++){ double x = arr[j] - arr[i]; double p = powl(2,j-i-1); double c = p * x; ans += c; } } ans /= powl(2,n-1); return ans; } // O(N) double solve2(vector<double> &arr){ double ans = 0; n = arr.size(); double ev_max = 0; double ev_min = 0; for(int i=0;i<n;i++){ double x = arr[i]; double p = powl(2,n-i-1); double c = p * x; ev_min += c; } for(int i=n-1;i>=0;i--){ double x = arr[i]; double p = powl(2,i); double c = p * x; ev_max += c; } ans = ev_max - ev_min; ans /= powl(2,n-1); return ans; } int main() { vector<double>arr = {1,1,2,3,4,5,7}; sort(arr.begin(),arr.end()); double ans1 = solve1(arr); double ans2 = solve2(arr); cout<<"ans1="<<ans1<<"\n"; cout<<"ans2="<<ans2<<"\n"; return 0; }

Comments (126)

Show archived | Write comment?

otaliptus

6 years ago, # |

← Rev. 2 →

Is this an easy problem about this topic?

→ Reply

brdy

For Paths in tree (2) can anyone (with spoiler maybe) explain how to do this with contribution method. For some reason centroid and dp solutions comes to mind but not contribution method.

Unless this is what is meant by contribution method in the context of the problem:

My idea

farmersrice

6 years ago, # ^ |

+21

check number of nodes on left side of edge

check number of nodes on right side of edge

edge contributes weight of (nodes on left side) * (nodes on right side) to sum

Kofta

4 years ago, # ^ |

Doesn't that approach counting some pathes more than one time?

No, why?

For example a tree of 5 nodes

Edges: (1, 2) (1, 3) (3, 4), (3, 5)

When i count the number of paths that passes through edge (1, 3), it will count path 1 -> 3 -> 4 as one of the paths

and when i count the number of paths that passes through (3, 4), it will count path 1 -> 3 -> 4 as one of the paths too

doesn't it count the same path more than one time or am I missing something?

Yes, the path is counted twice, since there are 2 edges, and therefore the contribution is 2. You don't add path lengths to the contribution, you only add the edge, which is +1.

I hadn't notice that he asked for sum of lengths not the sum of paths

that's clear now, Thank you

kanisht_09

7 weeks ago, # ^ |

I think first we need to calculate the subtree of size of node, i.e sub[i] = subtree size of ith node. The ans will be sum of sub[i]*(N-sub[i]) for all the N nodes of the tree.

vivek_shah

Thanks for such awesome blog.
I tried to work on above problems myself. For problem, Max of N under EV easy problem, I am not sure whether my approach is correct or not. So can someone please confirm, whether it's correct or let me know where I am going wrong.

Spoiler

Is it correct approach ?

Roundgod

← Rev. 7 →

One may use the basic definition for EV to find out the answer. Consider, what's the probability that the maximum outcome equals to x? That's not very easy to figure out. But instead, one thing is easy to figure out: the probability that the maximum outcome is less than or equal to x, which is just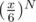 $\text{[math]}$ , let's denote it f(x), then the probability that the maximum outcome equal to x is just f(x) - f(x - 1), which I consider as one of the easiest ways to think of this problem.

UPD: The answer is therefore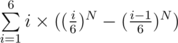 $\text{[math]}$ . You can then simplify it as you want.

Thanks a lot for sharing your approach!

Errichto

+12

Start in 15 minutes.

vijju123

-21

Very much looking forward to it — especially because its one of the new topics I am trying to be good at.:D

irishabhkhatri

5 years ago, # ^ |

Errichto I think you need to take care of your contribution LMAO.

GirGiti

-10

what is LMAO??

Not-Afraid

click

Brankonymous

Can somebody explain why test examples for this problem is 0.8 and 0.26?

If you have one probability 0.1 and other one 0.2 why it isn't 0.3?

hychyc

Because the problem asked the probability of Andrey not getting upset, in other words, the probability of Andrey getting exactly one answer. If you ask both of them, the probability of getting one answer is (A) the first gets the answer and the second doesn't, which is 0.1*(1-0.2) = 0.08, or (B) the first doesn't get the answer and the second does, which is (1-0.1)*0.2 = 0.18. Adding them up you get 0.26 chance not getting upset.

F16

Errichto Thanks for the lecture. The first few minutes of the video seems to be missing. Any chance of re-uploading the missing part.

After the stream, Youtube takes some time to dump/process the video and make it visible for later. Every time for a while only the last 2:00:00 are available. The whole thing is accessible now. (so after each stream you will have to wait some time to see the beginning again)

Is ans of Problem 8 in EV problem (which was left as homework) 8?

My working-

Lets call Expected value R.

Base case- We can get HH in first 2 tosses itself, with probability of $\text{[math]}$ .

$\text{[math]}$ (Not reduced purposefully).

Recurrence- If we dont get HH, then we used 2 tosses. The probability of not getting HH is $\text{[math]}$ , so with probability of $\text{[math]}$ we will get (2 + R)

Final Expression-

$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$

Is it correct? :)

Good approach, but you have a mistake. If the first two tosses are TH, then you can't say that you restart the process the EV of the remaining tosses is R. Instead, after the first T you should restart (after 1 toss in case of "TH").

Ouch! Yes, my bad! Thanks for feedback. I will try to get it right this time then :)

garnab27

Did you solve it finally? Is it R = 5 ?

Yes, I also got R=5. I think its time to request Errichto to reveal final answer now? :)

mno123

Answer is 6. I think you added expected tosses to get one H for TH. But it doesn't guarantee two consecutive H.

224

Ans is 6.

1/2 probability for T => 1/2(1+r)

1/4 probability for HH => 1/4(2)

1/4 probability for HT => 1/4(2+r)

r=1/2(1+r) + 1/4(2) +1/4(2+r)

so r=6

You can assume two different states, the initial state and the state where you already tossed one head. List two equations and solve them. You can find out that they are exactly the states in the AC Automaton. :)

Actually, there's a known formula first proposed by Solov'ev in 1966 for calculating the expected number of tosses needed until a certain pattern occurs in linear time combined with KMP algorithm. There's also a interesting game based on similar situations called Penney's game. I remember encountered one problem concerning Penney's Game in a CMU Contest in Ptzcamp. You can learn more about it if you are interested. :)

Linear time? Don't we need Gaussian elimination there?

adamant

Timus 1677. Doesn't seem to be solvable with gaussian elimination. Not straightforward at least.

Let's build KMP automaton. Now let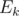 $\text{[math]}$ to be expected value of time you need to get from 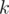$\text{[math]}$ -th state to the last one. Then 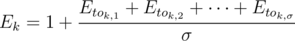$\text{[math]}$ , here σ is size of alphabet and 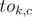$\text{[math]}$ is transition from k by letter c. Judging only by this, formula, I can say that it's solvable at least in O(n²) by Gaussian elimination because you have almost none elements above main diagonal...

You can also solve it in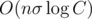 $\text{[math]}$ by binary searching E₀ and checking whether E_n turns out lower or greater than 1. It doesn't seem good since answer could be very large. So I'm curious how to solve it in linear time.

UPD: I got it! You should consequently express E₁, E₂, ... through E₀, this will solve the problem in O(nσ) at the end!

radoslav11

Nvm. You express E_i + 1 with the formula for E_i.

The thing is that k-th equation actually allow you to express (k + 1)-th term. Like, from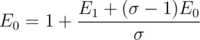 $\text{[math]}$ you can say that 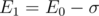$\text{[math]}$ , and so on you may keep it like $\text{[math]}$ .

← Rev. 3 →

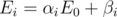Here's the formula: Say the pattern is A with length m, then we say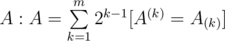 $\text{[math]}$ where A^(k) represent the suffix of length k of A while A_(k) represent the prefix of length k of A. Then the expected number of tosses until the first occurence of the pattern is just 2(A: A), which can obviously be computed in linear time, using, for example rolling hashes. I found this formula in Concrete Mathematics,Chapter 8, btw.

What about non-binary alphabet?

I guess it's just you replace the base by Σ where Σ is the alphabet size and at last multiply by Σ. Worked on a few examples, they all turned out to be right. :D

I think it can be proved using generating functions, as it was done for the binary case in Concrete Mathematics.

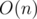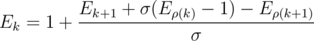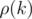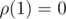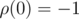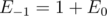Oh, I got another way to get $\text{[math]}$ solution. You can rewrite my initial formula as $\text{[math]}$ where $\text{[math]}$ is prefix function of first k letters with $\text{[math]}$ , $\text{[math]}$ and $\text{[math]}$ . This will allow you to write that $\text{[math]}$ .

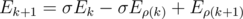Thank you. That gave me a new approach to try this- my previous approach got complicated because of TH case :(. Thanks for the resources :)

hocky

This is the exact solution first I thought of after seeing the One-Head Equation. The approach is dynamic programming like.

Let $$$R_{0}$$$ be the EV when your current sequence doesn't have any leading H, for example "...HTT_"
Let $$$R_{1}$$$ be the EV when your current sequence has 1 leading H, for example "...TTH_"

$$$R_{0}$$$ and $$$R_{1}$$$ can be written as:
$$$R_{0} = \frac{1}{2}(R_{0}+1)+\frac{1}{2}(R_{1}+1)$$$ (1st Equation)
$$$R_{1} = \frac{1}{2}\cdot1+\frac{1}{2}(R_{0}+1)$$$ (2nd Equation)

You can substitute the 2nd Equation to the 1st
$$$R_{0} = \frac{1}{2}(R_{0}+1)+\frac{1}{2}(\frac{1}{2}\cdot1+\frac{1}{2}(R_{0}+1)+1)$$$
$$$R_{0} = \frac{1}{2}(R_{0}+1)+\frac{1}{2}(\frac{1}{2}\cdot1+\frac{1}{2}R_{0}+\frac{1}{2}+1)$$$
$$$R_{0} = \frac{1}{2}(R_{0}+1)+\frac{1}{2}(2+\frac{1}{2}R_{0})$$$

Unable to parse markup [type=CF_MATHJAX]

$$$R_{0} = \frac{1}{2}R_{0}+\frac{1}{2}+1+\frac{1}{4}R_{0}$$$
$$$R_{0} = \frac{3}{4}R_{0}+\frac{3}{2}$$$
$$$4R_{0} = 3R_{0}+6$$$
$$$R_{0} = 6$$$

Yet, you can do not only two-heads, but a whole pattern match.

jenish9599

Problem 8:

Let's R be the EV.

Case 1: In first try, I got T, I wasted 1 move and the probability of this event is $\text{[math]}$ and the total number of flips required is R+1.

Case 2: In first try I got H and in second try I got T,So I wasted two moves,now the probability of this event is $\text{[math]}$ and the total number of flips required is R+2.

Case 3: I got HH, I am done in 2 moves with probability $\text{[math]}$ .

So, Final Expression:

$\text{[math]}$

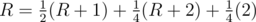
So after solving this we can get R = 6.

Is this correct ??

Yes, it is — https://ideone.com/J3bAiY.

rawnix

My (more complicated) approach:

$$$R = \frac{1}{4}(2) + \frac{2}{4}(2+R) + \frac{1}{4}[2+\frac{1}{2}(1)+\frac{1}{2}(1+R)]$$$

The first term is for the case when we get HH in the first two tosses with 1/4 probability and using two tosses.

The second term is for the cases TT and HT in the first two tosses with combined probability 1/2 and two wasted tosses plus the expected number of tosses to get two heads in a row.

Now, when we get TH in the first two tosses with 1/4 probability, we have already wasted two tosses. After these two tosses, we can get H with half probability (thus we have used one more toss), and we can also get T with half probability (one toss is wasted plus the expected number of tosses to get two heads in a row).

On solving, we'll get the answer R = 6.

allllekssssa

How to find the sum over squares of lengths of paths?

I know only with FFT, but for sure there is some nice solution.

-14

He discussed this in the later part of his stream. The basic summary was, that, for each edge, we count number of path it belongs to. (It might seem unintuitive at first, but take it like this- The approach needs all edge weights one, length of path is nothing but number of edges in it, and we are summing up how many paths this edge belongs to.)

So, he derived a formula that-

For each edge, if there are U nodes down the subtree, answer for that edge will be -

E_i = U * (N - U) (Number of nodes in sub-tree *Number of nodes outside it)

Summing this for all edges gave the answer. You can root tree at any arbitrary vertex.

Thanks for explanation!

But, I thought about sum over squares of lengths of paths. It is more complicate for me.

Sorry! Misread your question. Too late to delete that comment now... will be more careful. I m also stuck on that bonus one :(

AnonymousBunny

+13

There is nice direct trick for this, not related with expected values.

First, calculate squared distance from the root to all other vertices. Now perform dfs on the tree and when you enter vertex u you should add 1 on its subtree and subtract 1 for all other vertices. When you leave the vertex, you should do vice versa. Thus, at all times you'll be having distance from current vertex to all other vertices and you can easily do thingls like calculate sum or even sum of squares of distances to all other vertices.

It works in $\text{[math]}$ and only thing it requires is segment tree + Euler tour to make 1-1 correspondence between segments in array and subtrees in tree.

I actually gave problem on that in hackerrank week of code 23, link :)

← Rev. 4 →

I think this problem is solvable in O(nm) if we are required to compute the sum over mth power of lengths of paths. Let dp_v denote the answer for subtree rooted at v, so we basically need maintain a set of numbers with the following three operations: 1. merge two sets 2. add 1 to every number in the set 3. query the sum over mth power of the numbers in the set. If we maintain the sum of ith power for the numbers in the set for every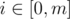 $\text{[math]}$ and compute the dp values using the formula 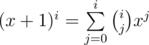$\text{[math]}$ , it would result in a O(nm²) solution. However, we can maintain the ith descending powers power for the numbers in the set for every 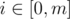$\text{[math]}$ , and use the simple formula 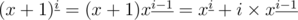$\text{[math]}$ , the dp can be calculated in O(nm) time, and we can precompute Stirling numbers of the second kind in O(nm) and use the formula 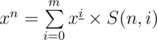$\text{[math]}$ to recover the answer.

You need more than that from the structure. Please specify how exactly are you going to calculate answers?

P.S. I think it won't solve problem from hackerrank

OK. I was just talking about the problem that asks one to find out the sum over mth power of lengths of paths for a tree. To be specific, we store dp_v, i the sum over the ith descending power of the length bewtween all vertices in the subtree of v and v.

But what about overtree of vertex? I guess, you're doing some new dfs, keeping it on the stack?..

Yes. You need two dfs, one from top to bottom, and one from bottom to top, just as many tree dp problems require, and what you eventually get for each vertex v is the sum over mth power of lengths of paths with one end at v. Summing up and dividing by two will yield the answer.

Lixoskywalker

For the special case with unweighted edges, we can solve it in O(n * (log²(n) + log(m))) using centroid decomposition and FFT.

I have never managed to code it properly, though.

ILoveBitches

allllekssssa how to solve it with fft? Thanks.

tdas

Use centroid decomposition, encode every child-subtree of the node we are fixing in CD as a polynomial, find the product of this polynomials, the i-th coefficient of the product is the amount of paths that pass through the node we are fixing and have size i.

soul_voyage

For Q1 P(getting an ace) = (C(4,1) + C(4,2) + C(4,3) + C(4,4))/C(52,10) Is this correct?

greatindian

You can consider each of the cards individually and calculate their contribution. For eg the 1st one has a probability of 1/13 to be an ace. Similarly, you can carry out the process for 10 cards: (1/13)*10=10/13.

Why is probability of getting an ace by picking 10 random cards at once should equal to P(geeting an ace) by picking one by one cards 10 times?

You are drawing cards from a shuffled deck so the order does not matter while considering 10 cards. You don't have to worry whether the first card is an ace or not. For eg: what is the probability of 2nd card to be an ace when you don't know what the 1st card is: 1/13. Similarly using linearity of EV you can cover all the cases.

dmkz

I think, that this solution is incorrect, because in your solution and Errichto solution probability of 5 aces in 10 randomly picked cards = $$$(1/13)^5$$$ greater than zero, but should be equal to zero.

UPD. Buuut this is brute force for 5 randomly picked cards, and answer is $$$(1/13) \cdot 5$$$, I don't understand why it works correctly

+15

How does my solution say what is p-bility of 5 aces?

The solution is to use the linearity of expectation. The expected value of results of 13 events is equal to the sum of expected values of each of them, even if they are not independent.

Am I correctly understand, that you are include all probabilities in single event, then you know only expected value for one event and nothing about probabilities, and successfully get correct answer?

+10

I know a probability that the 7th card is an ace. It's $$$1/13$$$. This means that in $$$1000$$$ games, around $$$1000/13$$$ times (on average) I will get an ace from that card. Same for 1st card, 2nd card, and so on.

Yes, I don't care about p-bilities of having exactly some number of cards. That would lead to more complicated computations.

Ok, I understood, thanks for your answer

B_Consistent

11 months ago, # ^ |

How are we picking a card 1000 times without replacement in a deck of 52 cards
Doesn't average moves to 4 since they are 4 aces ?

armoking

My bad — I misunderstood your solution and tried convince dmkz that mistake in it :D
Well, there is another way to find correct answer. Let's mark all aces like a units, all other cards like a zeros.
Now, let's modulate current situation. You have a sequence of 4 units and 48 zeros. You wanna know — EV of quantity of units in first 10th numbers of permutation.
EV = P(x = 1) * 1 + P(x = 2) * 2 + P(x = 3) * 3 + P(x = 4) * 4
So it easy to proof, that P(x) in this case is equal to C(10, x) * C(42, 4-x) / C(52, 4), where C(n, m) = n! / (n-m)! / m!
So... the answers is the same)

How dare you ;p

Yeah, you can solve EV problems two ways usually: by definition like you did, or by linearity.

manish_joshi

How to solve the last part of Question 9 Volleyball ? I feel like it is somehow related to Bayes' theorem, but i am unable to calculate the expected wins of the winner.

In 9th question on volleyball, expected number of total matches won by winner = 3 + expected number of matches won by winner in group stage. What is expected number of matches won by winner in group stage? Is it 11/8

jimmy51997

https://codeforces.me/problemset/problem/601/B — Also a problem of Contribution technique (after being decomposed into simpler form). Try this out guys.

itachi_god

guys can anyone explain how to solve this question: link:https://www.codechef.com/AMR18ROL/problems/MARTING1

master_me

Can someone please explain the solution of Eating Ends? I can't understand the no. of ways for an element to remain till last.

shaanknight

For the 9th question of EV easy problems, is the answer to the problem EV of the number of matches won by the winner of the whole tournament 29/6 ?

There is a video with timestamps to each problem.

You are talking about the homework problem, right? I found the answer to be $$$35/8$$$.

The winning team has obviously won 3 matches (quarter-final, semi-final, and the final matches).

Now we only need to find the expected number of matches won in the group by a team given that the team advanced into the elimination stage ( we'll call this value $$$EV_2$$$, so $$$ EV = 3 + EV_2 $$$).

We can use Bayes' theorem for this.

Let's call $$$P(adv)$$$ the probability that the team advanced into the elimination stage. By symmetry, $$$P(adv) = 2/3$$$. Also, let $$$P(x)$$$ be the probability that the team won x out of 2 matches played in the group.

Now, $$$ EV_2 = 0 \cdot P(0|adv) + 1 \cdot P(1|adv) + 2 \cdot P(2|adv) $$$

No team can advance into the elimination stage by winning 0 out of 2 matches, so $$$ P(0|adv) = 0 $$$. This also implies $$$ P(1|adv) + P(2|adv) = 1 $$$

According to the bayes' theorem,

$$$ P(2|adv) = \frac{ P(adv|2) \cdot P(2) }{ P(adv) } $$$

We know that if a team wins 2 out of the 2 matches played in the group, it is definitely going to advance. So, $$$ P(adv|2) = 1 $$$. This gives us

$$$ P(2|adv) = \frac { 1 \cdot \frac{1}{4} }{ \frac{2}{3} } = \frac{3}{8} $$$

Also,

$$$ P(1|adv) = 1 - P(2|adv) = \frac{5}{8} $$$

Hence we get $$$ EV_2 = 1 \cdot \frac{5}{8} + 2 \cdot \frac{3}{8} = \frac{11}{8} $$$

Finally adding 3 to this we get, $$$ EV = \frac{35}{8} $$$

Please correct me if I'm wrong.

KingInTheNorth_

Yes, this is right, here is the monte carlo simulation.

gupta_samarth

5 years ago, # |

← Rev. 9 →

Hi. Just like EV easy problems 6-8, how to solve something flipped (updated) like Calculate Expected Value of "Number of consecutive triples of Heads" in $$$N$$$ coin tosses.

My approach, Let $$$R_n$$$ be required result for $$$n$$$ coin tosses. Then, we have that Case 1: if $$$nth$$$ toss is Tails, then we need to add $$$R_{n-1}$$$ to answer.

Case 2: if $$$nth$$$ toss is Heads, then we need to consider two cases again, if $$$n-1th$$$ toss is Tails, we add $$$\frac{ R_{n-2} }{2}$$$ to answer, if $$$n-1th$$$ toss is Heads then again if $$$n-2th$$$ toss is Tails then we add $$$\frac{R_{n-3}}{4}$$$, else we add $$$\frac{1 + R_{n-3}}{4}$$$.

So, $$$R_{n}$$$ = $$$R_{n-1} + \frac{R_{n-2}+R_{n-3}}{2}+ \frac{1}{4}$$$. It doesn't seem right to me. Also, since $$$R_0=R_1=R_2=0$$$, we get $$$R_3=\frac{1}{4}$$$, and $$$R_4=\frac{1}{2}$$$. So, basic examples do seem ~~correct~~ incorrect. Can someone verify this and/or give a different, perhaps easier approach. I like to ask for verification, because when I do so many cases, I always feel like I have done something wrong. Thanks a lot in advance.

UPD: Obviously incorrect, because $$$R_3=\frac{1}{8}$$$.

UPD2 : I think I found the error, I missed the multiplier of $$$\frac{1}{2}$$$ for $$$nth$$$ toss. So that makes it $$$R_n = \frac{R_{n-1}}{2} + \frac{R_{n-2} + R_{n-3}}{4} + \frac{1}{8}$$$. Now all I need for satisfaction, is to solve this recurrence with $$$R_0=R_1=R_2=0$$$ and get the formula provided by Errichto. ( Substitution of formula in place of $$$R_n$$$, for sufficiently large $$$n$$$ (such that we don't have to worry about max function ) does not satisfy the recurrence. ) Can someone point out what's wrong with this approach, thanks.

The EV of the number of consecutive triples of heads in $$$N$$$ coin tosses is $$$max(0, N - 2) \cdot \frac 18$$$ — each of $$$max(0, N - 2)$$$ consecutive triples of tosses has pbility $$$\frac 18$$$ and we use the linearity of expectation. But your formulas look strange.

Problems 6-8 are about the EV of the number of tosses till something happens, not the EV of the number of heads/whatever.

Yes, I know problems 6-8 are entirely different. Infact I wanted to flip it around. But how did you use linearity again?

Did you break it linearly on the starting positions of the triple? That explains $$$max(0,N-2)$$$. Cool. Thanks a lot.

Yes, you can think about it as the number of ways to choose the starting position of three consecutive tosses. But my definition was also enough — the number of ways to choose three consecutive tosses.

I think I figured out where it falls short, even after considering possibilities for last 3 tosses, we need to consider fourth last toss, so as to not forget counting triples formed from fourth last toss and some of last three except last as ending of the triples.

There is a training, contains 13 problems on probability theory and expected value, 10 of them published on codeforces and can be solved, 3 problems (A,B,C) for beginers can be solved on e-olymp: A. Difficult path, B. A coincidence, C. A full set.

harshhx17

Game on Trees, a nice problem on this topic.

Though I understood the solution better by thinking in way of contribution rather than Linearity of Expectation.

derrick20

Could someone just go through some/all the bonus parts so that I can have something to check my ideas with?

singhpriyank

A nice problem on expected value Your text to link here...

Ice_Cream

In Volleyball Find EV of the number of matches won by Poland, assuming that they won the whole tournament. I think the answer to the above question will be E(won by Poland) = E(won by Poland in the group stage) + E(won by Poland in the tournament) = 1 + 3 Is that right?

And the other question the EV of played matches of Poland will be E(played matches of Poland) = P(Poland lose in group stage) * 2 + P(Poland lose in the quarter-final) * 3 + P(Poland lose in the half-final) * 4 + P(Poland lose in the final) * 5 + P(Poland won the final) * 5 = 1/3 * 2 + 2/3 * 1/2 * 3 + 2/3 * 1/2 * 1/2 * 4 + 2/3 * 1/2 * 1/2 * 1/2 * 5 + 2/3 * 1/2 * 1 / 2 * 1/ 2 * 5 = 19/6 And I think the symmetric solution is quite elegent. Cool solution. Thanks to your blog

EV(won in group stage) = 1 is true for a team that we know nothing about. If Poland won the whole tournament, then we know they passed the group stage. This is some conditional probability (well, conditional EV). That EV should be slightly bigger than $$$1$$$.

Everything else in your post is correct, I think.

Your computation of P(x=1&tie|won) is strange, same for P(x=1&noTie|won). You seem to skip the assumption that they won.

Sorry for above, I re-did the calculations and got same result same as https://codeforces.me/blog/entry/62690?#comment-570262 and got 11/8 for E(no. of won in GS | won in the tournament), can you please point out what is wrong in there,

Is it wrong though? That's a long comment to analyze. What should be the answer? (I don't remember now)

you told here http://codeforces.me/blog/entry/62690?#comment-560466 answer will be 1 for EV(no of won in GS | won the tournament). Can you please explain the logic here?

Nope. I said: "EV(won in GS) = 1" is true for a random team. If you won a tournament, your EV is slightly bigger than 1.

So what should be the answer for "EV of the number of matches won by the winner of the whole tournament"

I don't remember. Write a program to check that ;) simulate the tournament 10000 times and take the average result. This is called Monte Carlo method.

Thanks for helping out, the two live streams on EV and exchange arguments were really helpful.

kocko

If anyone is interested, this article contains some nice examples (with exercises) of how to calculate the EV with some generalizations, as addition.

In the first problem, the expected value of number of aces, when 10 cards are drawn at random without replacement will be different than the EV when the cards are drawn with replacement.

Is this correct?

No. In both cases, the probability of an ace in $$$i$$$-th card is $$$1/13$$$ for every $$$i$$$, so the answer is $$$10 \cdot 1/13$$$.

For some reason, my mind was just not accepting this, so I calculated the answer in a brute force way, and was amazed to find the answer to be the same.

I find it quite astonishing that the answers are same for both the cases however both the cases look so different! For eg:- In "with replacement" case, the maximum number of aces you can draw is 10, where as in "without replacement" case, it is only 4.

Thanks a lot for this article and video!

If you toss a coin 10 times, you will get 5 heads on average.

If you toss a coin once and then write down the same result 9 more times, you will again get 5 heads on average (in those 10 results, that each is the same).

izban

But we all know that you should toss a coin to your witcher.

Trgt_2021_explosion

This is exactly where I am stucking — you are saying it is $$$1/13$$$ for every $$$i$$$. But How? For example If I got all 4 aces in the first 4 places itself then there is no ace in 48 cards remaining. Then how it's probabilty is $$$1/13$$$ for $$$i$$$ in range $$$[5,10]$$$? Please clarify this to me. Anyone?

For example If I got all 4 aces in the first 4 places

But you didn't get those aces. You don't need to compute EV under the condition that something happened in the first few moves. If I draw 10 cards in a row and don't tell you what are first nine cards, do you think the probability of tenth card being an ace isn't $$$1/13$$$?

Yess. Thank you. It means I was not knowing the defintion of Random selection. It means that in Random selection every selection is like first selection because we don't know what is the selection we have made so far. If I am wrong in this interpretation then please point it.

It seems that you treat "random selection" as some particular term with a definition. Nah, this is real life. If you now need to bet on the outcome of drawing a 10-th card, every value (2,3,...,ace) is equally likely so it's $$$1/13$$$, done. Here, we care about the probability for "10-th card being an ace".

It's more complicated to compute the probability for two cards being aces or "5-th card is ace, 10-th card isn't". But then you still shouldn't worry about the cards revealed before revealing those two cards you care about. You compute probability now.

There are thousands of articles, books and videos about probability. You should go through some to get a better understanding of the topic.

ben_dover

From a statistical perspective the important thing about linearity of expectation is that the variables do not need to be independent for linearity of expectation to hold.

Example from https://brilliant.org/wiki/linearity-of-expectation/

"Let that sink in for a moment, as it can be quite counter-intuitive! As an example, this means that the expected value for the amount of rain this weekend is precisely the expected value for the amount of rain on Saturday plus the expected value for the amount of rain on Sunday, even though we do not think that the amount of rain on Saturday is independent of the amount of rain on Sunday (for example, a very rainy Saturday increases the likelihood of a rainy Sunday)."

So even if $$$X$$$ and $$$Y$$$ have some interaction (not independent), we can still decompose expectation of $$$X+Y$$$ into components expectation of $$$X$$$ and expectation of $$$Y$$$.

Here is another example. Suppose you flip 6 coins. Let $$$X$$$ be the RV that counts the number of heads from the first three coins (coins 1, 2, 3). Let $$$Y$$$ be the RV that counts the number of heads from the odd numbered coins (coins 1, 3, 5). Clearly $$$X$$$ and $$$Y$$$ are not independent, because intuitively given a high value of $$$X$$$ a high value of $$$Y$$$ is more likely. Formally $$$P(Y=y) \ne P(Y=y|X=x)$$$. But we can still calculate the expectation of the sum by considering $$$X$$$ and $$$Y$$$ independently. $$$E[X+Y] = E[X] + E[Y]$$$

towrist

4 years ago, # |

If anyone is struggling (like I did) to find the actual rigorous meaning of a Random Variable, and what it means actually to "find the sum" of two random variables, here goes:

First of all, random variable is not AT ALL a variable. That's a very misleading name, and for me, was the source of much confusion. A random variable $$$X$$$ is defined as a function which maps occurrences to real values (at least in the scope of Competitive Programming). What it means that $$$X:S->R$$$ , where $$$S$$$ is the sample space, takes in an outcome (an element of the set $$$S$$$) as input and outputs a real value (an element of the set $$$R$$$). The function is defined according to the given problem. For example, if we want to find the "expected number of pips" in a dice throw, the function $$$X$$$ returns the number of pips in the occurrence.

Then what does it mean to add two random variables? If we define $$$X=X_1+X_2$$$, where $$$X_1$$$ and $$$X_2$$$ are two random variables, then $$$X$$$ is actually the composite sum function. This just means that for each occurence $$$w \in S$$$,

$$$X(w)=X_1(w)+X_2(w)$$$. (This is the definition of composite functions.)

Now, about the notation $$$P(X==x_0)$$$: Note that it is not obvious what it should mean, unless it is defined. We shouldn't just use our intuition to guess the meaning of symbols. This is because the $$$P$$$ function is defined only for events (you should read up on Axioms of Probability Theory if you are not sure about the exact definition of Probability itself), and it is not clear what $$$X==x_0$$$ even means.

Let $$$E$$$ be an event (an event is a subset of sample space, so each element of the set "event" is an occurrence. I used to mix up events and occurrence so here was a gentle reminder) consisting of all occurrences $$$w$$$ such that $$$X(w)==x_0$$$. Then $$$P(X==x_0)$$$ is defined as $$$P(E)$$$. So $$$P(X==x_0)$$$ can now be read as the probability of the event that the occurrence has preimage (output of a function) equal to $$$x_0$$$ for the function $$$X$$$.

For the definition of Expected Value of a Random Variable and a very simple proof of linearity of expectation you can click here

I am sorry if all of this is very obvious to experienced coders, but I wanted to put at one place all my thoughts about various definitions and results about random variables.

antontrygub

You know, I was recently looking for something like this. I have starred your comment into my favorites, thanks!

Glad to be of help ^_^

ritik_patel05

I didn't quite understood the dp approach for problem 4. Max Of N in EV Easy Problems. If anyone can explain, Thank you!

rgalpha

3 years ago, # |

What is the solution to the total no of matches won by the winner of the tournament? My attempt till now: The winner must win quarter-final, semi-final and final. So we need to only find expected no of matches won by a qualifying team in group stage.

To find that, I wrote all the cases (assuming team A is the team required to qualify and matches are in order AB BC and CA). A qualifies in the following cases: A B A (winners in order), A C A, B B A, A C C, A B C (followed by random selection of A), B C A (followed by random selection of A)

So the expected no of wins in group stage is: 2*(1/4) + 1*(1/4) + 1*(1/4)*(2/3) = 11/12. But this seems wrong because: Total wins = 3. And both qualifying teams will have same expected no of wins. So expected number of wins of not qualifying team = 3-2*(11/12) = 14/12 which is greater than 11/12.

I am surely missing something. Any help would be appreciated :)

3 years ago, # ^ |

1) You listed down six cases of A winning and I don't see how your formula considers all of them.
2) It seems that you computed "EV of A' wins but we don't count anything if A doesn't pass". You need to then divide it by "probability that A passes" in order to get "EV of A' wins if we know A passes".

Thank you for the prompt response. I understood my mistake. I also found the following link on conditional expectation helpful for better understanding: link

QuickAndSteady

Errichto I am having trouble in solving a particular type of expected value problems. In problems, where we move from one state to another with some probabilty and when we reach a special state, we are taken back to the initial state(the state from where we started), I am unable to take into account the part where we move to the initial state. I couldn't find any relevant resource to learn this concept. It would be very helpful if you could give some insight or briefly explain the generalized approach for these kind of problems.

Two problems related to the above concept:

ABC189_f

Codedrills_ICPC_Practice_Session_6

It would be very helpful if anyone can help me with this concept. Thanks in advance!

Kaey

I'll try to explain it with a simpler example. You have to calculate the ev of the number of coin tosses it takes to get heads once. You can notice that if you get tails you "restart" the game. If you call the EV $$$x$$$, you have that $$$x=1/2+(x+1)/2$$$, since there is $$$1/2$$$ probability to end the game in one toss and $$$1/2$$$ probability to repeat the game, which will end in $$$x$$$ moves on average. You can then easily solve the equation. This very same concept can be applied to the ABC problem.

dgupta0812

I also get confused in problems involving this concept. It would be great if someone can provide resources to understand such concepts and few problems to practice.