Hello, codeforces!
Sorry for the long break, but the last weeks of holidays and the first weeks of academic year took my attention. I hope today's trick will make you forgive me. :P
I invented this trick a few years ago, but for sure I wasn't first, and some of you already know it. Let's consider the following interactive task. There are n (1 ≤ n ≤ 105) hidden integers ai, each of them from range [1, 1018]. You are allowed to ask at most 103000 queries. In one query you can choose two integers x and y (1 ≤ x ≤ n, 1 ≤ y ≤ 1018) and ask a question ''Is ax ≥ y?'' The task is to find the value of the greatest element in the hidden array. The checker isn't adaptive.
Unfortunately, this task is only theoretical, and you cannot solve it anywhere, but it'll turn out, that solution can be handy in many other, much more complicated problems.
Even beginners should be able to quickly come up with a solution which asks n·log(d) queries (where d = 1018). Unfortunately, this is definitely too much. The mentioned solution, of course, does n independent binary searches, to find each ai.
Some techniques come to mind, for example we could do all binary searches at the same time, ask for each element if it's greater than 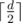 , or something, then forget about lower values... but no, things like that would aim only at really weak, random test cases. More, it seems that they wouldn't work on a first random max-test.
, or something, then forget about lower values... but no, things like that would aim only at really weak, random test cases. More, it seems that they wouldn't work on a first random max-test.
The limit on the number of queries slightly higher than the limit on n should give us a hint: for many elements of the array, we should ask about them only once (of course we have to ask about each of them at least once). So, maybe let's develop a solution which at least has a chance to do it. Here comes an idea: let's iterate over numbers in the hidden array like in the n·log(d) solution, but before doing the binary search, ask if ai that we are looking at right now is strictly greater than the greatest value that we've already seen. It is isn't, there is no point in doing the binary search here — we are only interested in greatest value.
Of course, this solution can do the binary search even n times, for example when the hidden array is increasing. Here comes a key idea: let's consider numbers in random order! It would definitely decrease the number of binary searches that we would do, but how much? Let's consider the following example (and assume that numbers are already shuffled):
10, 14, 12, 64, 20, 62, 59, 39, 57, 96, 37, 91, 88, 5, 76
A filled circle means that we do the binary search, an empty circle means that we skip this number.
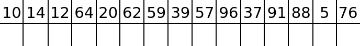
Of course, we should do the binary search when the prefix maximum changes (increases, in particular, it can't decrease). How many times will it happen on average? Let's focus on the global maximum. It's clear that for sure we have to do the binary search to find its exact value and that we won't do binary search anymore to its right. What with elements to its left? The situation turns out to be analogical. Where will be the global maximum in a shuffled array? Somewhere in the middle, won't it? So, we'll do the last binary search in the middle (on average), one before last in the middle of the left (on average again) half and so on. Now, it's easy to see that we'll do the binary search only O(log(n)) times! A total number of queries will be equal to n + O(log(n)·log(d)), which seems to be enough. It also can be proven or checked with DP/Monte Carlo, that probability that the number of binary searches will be high is very low.
OK, nice task, randomized solution, but how could it be useful in other problems? Here's a good example: 442E - Gena and Second Distance. Editorial describes the solution, so I'll mention only the essence. We want to maximize some result, and we have n ''sources'' that we can take the result from. In each of them we do the binary search to find the highest possible result from this source, and then we print the maximum of them. Looks familiar? The most eye-catching difference is that in this task we have to deal with real numbers.
Experience tells me that this trick is in most cases useful in geometry. It also reminds me how I discovered this trick: when I was solving a geometry problem in high school and trying to squeeze it in the time limit. I decided to check if current ''source'' will improve my current result and if not — to skip the binary search. It gave me many more points (it was an IOI-like problem) even without shuffling sources. Why? Test cases were weak. :D
So, did another blog about randomization satisfy your hunger? If you know more problems which could be solved with this trick, share them in the comments. See you next time! :D











This is maybe the coolest trick I've ever seen. Radewoosh told me this thing a few years ago and it helped me get a few AC's since then. I strongly recommend reading and understanding it well.
also: a gif, hurray!
I have
stolenset a problemfrom Cormen's bookwhere you have to find a second maximum in the array: 101149M - Ex Machina. This problem is not hard and has easier solution without this trick, but the trick is appliable.And what's the solution?
Find the first maximum using single elimination bracket. Second maximum is one of elements which has lost to the first maximum.
Hey dalex! I just solved the problem "normally" (the intended solution i guess) and it got AC in 46ms. I tried shuffling the indices just to try and it got AC in 62ms. I'm guessing that's not the point of the trick, right? How would you apply the trick on this problem? Thanks!
Normal solution is in my spoiler above.
And the solution with trick is:
Shuffle numbers, go through them, maintaining two maximums. Compare each number with second maximum first — most likely it will be less than second maximum, so no need to compare it with first maximum.
Aaah got it, i was thinking the whole time i was going to do 2*N queries, but i forgot the whole point of the trick, the random shuffle, lol. It got AC in the same time as the original solution, but it's easier to code and you can clearly see why it works.
Cool example, thanks dalex!
How do you simulate the shuffling of the hidden array?
I think by randomly choosing the position of the array where you do each query
vector<int> indices{0, 1, 2, ..., n-1}; random_shuffle(indices.begin(), indices.end());Is this hackable in the same way as some other randonized algorithms only with srand(0)?
Use std::mt19937.
See https://en.cppreference.com/w/cpp/algorithm/random_shuffle
Thank you!
Why global maxima will be always somewhere in the middle and how will maximum number of binary searchies be logn?
Not always. But the expected value of its position will be in the middle.
Here is some good intuition to why the element is probably in the middle: For every position, compute the average distance to all other positions, the element that is “closer” to all others is the middle
I was a little doubtful that this would work (due to the randomness). So I tried to simulate the checker program and the algorithm described in your blog. It works after all! I learnt a great deal today! Thanks Radewoosh!
Here's the actual proof:
Consider En as expectation of number of changes of the maximum in every prefix.
by considering the position of the maximum we get:
using two equations above we get:
so we proved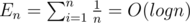
Okay, that's expected value, but more interesting thing is distribution. Like, what's the probability of taking k·En instead of En? Markov's inequality suggests it's at most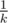 , but maybe there is some better estimate?
, but maybe there is some better estimate?
Well, just an idea: assume that the sequence is a permutation. If you take Xk as the random variable indicating whether we have a prefix maximum at the k-th position, then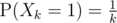 , and X1, X2, ..., Xn are all independent. A way to see it: if you have a permutation on k - 1 numbers, you can create k permutations on k numbers by picking the last element and taking the remaining numbers to preserve their relative order. The k-th element is the largest in exactly one of them.
, and X1, X2, ..., Xn are all independent. A way to see it: if you have a permutation on k - 1 numbers, you can create k permutations on k numbers by picking the last element and taking the remaining numbers to preserve their relative order. The k-th element is the largest in exactly one of them.
Having that, you could probably try to approach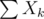 with some Chernoff bounds (hopefully I didn't do anything fundamentally wrong here):
with some Chernoff bounds (hopefully I didn't do anything fundamentally wrong here):
I'll assume for simplicity that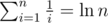 , the real result won't be far off. We have
, the real result won't be far off. We have 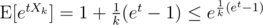 , and therefore
, and therefore 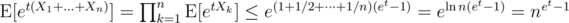 . Now, for any δ > 0 and t > 0, Chernoff gives us
. Now, for any δ > 0 and t > 0, Chernoff gives us 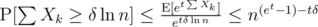 , minimized at
, minimized at 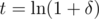 , which gives us
, which gives us 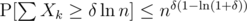 . For instance, for δ = 4, we have
. For instance, for δ = 4, we have 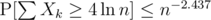 .
.
For our bounds, we can afford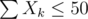 . When we plug in n = 105, δ = 4.34, we arrive at
. When we plug in n = 105, δ = 4.34, we arrive at 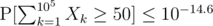 . And it's probably way lower than that.
. And it's probably way lower than that.
Edit: turns out I'm not that far off. A simple dp shows that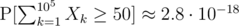 .
.
I was anticipated.
We are going to study the distribution. Some math is involved, come prepared.
Given a random permutation , let Xi be the random variable that has value 1 if σ(i) > σ(j) for any j < i and 0 otherwise. Our goal is to study the distribution of X1 + ... + Xn.
, let Xi be the random variable that has value 1 if σ(i) > σ(j) for any j < i and 0 otherwise. Our goal is to study the distribution of X1 + ... + Xn.
The first remark is that the random variables Xi are independent. This can be proven noticing that Xi depends only on the set of values in {σ(1), ..., σ(i - 1)} and on the value of σ(i). But this two information are independent from Xj for any j < i.
Furthermore, it is very easy to compute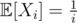 and
and 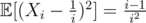 .
.
Having shown that the variables Xi are independent and having computed their expected value and variance, we can apply Bernstein Inequality on the random variables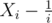 . Exploiting that
. Exploiting that  , if we plug in t = (λ - 1)Hn with λ > 1, Bernstein inequality tells us
, if we plug in t = (λ - 1)Hn with λ > 1, Bernstein inequality tells us
that is much stronger than the bound that you were suggesting. For example, if n is sufficiently large (like n ≥ 100), the above inequality implies
that you were suggesting. For example, if n is sufficiently large (like n ≥ 100), the above inequality implies
Let me add that it is very natural to apply Bernstein inequality when trying to bound the tail distribution of a sum of independent random variables. In some sense, Bernstein inequality is the correct version of Markov inequality. Indeed Markov inequality is extremely far from being optimal in almost any situation where the variables are independent, whereas Bernstein gives an almost sharp estimate quite often. The proof of Bernstein inequality is more involved than the one of Markov inequality but still elementary. If you want to learn it, take a look into A gentle introduction to concentration inequalities, specifically Section 4.
Although I have absolutely no idea how to work this out... since the maximum element is in a random position with equal distribution, then the expected value and the distribution in total are exactly equal to the depth of quicksort.
I trust quicksort, So I don't prove :).
Have been waiting for your blog, big thanks that you keep doing it!
:O
If community generally dislikes whining, it probably should also generally dislike bragging :)
P.S. I don't imply anything
Could someone explain how to solve the "almost a typical problem" mentioned in the editorial? I'm bad at geometry but me and kllp thought about this a lot yesterday and couldn't figure out how it can be done.
I mean this part: "Finding such point is almost a typical problem which can be solved in O(klogk) where k — number of intersections points of circles"
I think it should be done the same way you can find two closest points in the given set. Either do divide&conquer or sweep from left to right, and maintain recent points on set, sorted by y. When we have a new point (x, y), in set check everything with values from y - 2·R to (y + 2·R).
Thanks for the great idea!
I read about similar idea in some old Russian blog in a comment. The task is to find a minimal covering circle for a set of points, and it can be done in linear time with a help of shuffling points.
hmm, thought this trick is well known, first time meet them like 5 years ago in preparing tests for problem
and it close to another geometry feature: convex hull of random 2D points is O(logn)
And O(logd - 1(n)) in d dimensions.
And if you choose them uniformly from a disk, it's O(n1 / 3) (article).
You can do it in o(n) with a pivoting algorithm right? Like finding the median element.
Here's another way at looking at this trick, not sure if it actually makes mathematical sense :)
Suppose we have checked i numbers in random order and the maximum so far is m. For the next number, we would normally binary search between m and 1018. However, we know that it's quite likely that the next number is less than or equal to m — that happens with probability at least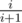 . So we need to do binary search with weights: m has weight
. So we need to do binary search with weights: m has weight 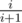 , and the numbers between m + 1 and 1018 have weight
, and the numbers between m + 1 and 1018 have weight 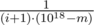 .
.
The optimal way to do said binary search boils down to exactly the algorithm you describe.
It is the same as insert 1, 2, ..., n into a treap with priority are shuffled_a[1], shuffled_[2], shuffled_a[3], .., shuffled_a[n].
Is it rated?
Is it a joke?
emm···emm···emm···emm···
Can anyone kindly explain how the numbers of binary search is O(logn)? Maybe I am facing difficulties getting the places where the binary searches should take place.
The blog says : " Some techniques come to mind, for example we could do all binary searches at the same time, ask for each element if it's greater than , or something, then forget about lower values... but no, things like that would aim only at really weak, random test cases. More, it seems that they wouldn't work on a first random max-test. "
Techniques like " taking a [d/2] and checking each ai if ai >= d/2 and continue filtering elements, till you have one element and do binary search to get its value " works only on weak, random test cases, can someone provide a corner case where this method fails I feel this technique may work
A simple case is all elements of array a with same value.
For array a with distint elements we can build array {1018 - 99999, 1018 - 99998, 1018 - 99997, ..., 1018} of size 10^5 and you would only discard elements at the last steps of binary search.
That`s a very good trick, thanks!
Really cool! It works for yesterday's F
https://codeforces.me/contest/1101/problem/F
Edit: ok it's now in the editorial https://codeforces.me/blog/entry/64483
Thanks for this blog and it makes me came up with a strange idea:) It means that the length of increasing subsequence that include the maximum number is O(log n) in average.And I have been known that the LIS of a permutation is O(sqrt(n)).Then I want to know that how many permutations that one of the LIS's ending is number i? For example,for n=3,there is 1 permutation for number 1 (3 2 1),and 2 permutations for number 2 (1 3 2 and 3 1 2), and 5 permutations for number 3 (exclude 3 1 2).
This useful technique also appears in this paper: "Geometric Applications of a Randomized Optimization Technique".
In case someone is having a hard time understanding the time complexities of randomised algorithms/data structures, there's a pretty cool paper called 'Randomized Reduction', by Brian Dean, which uses the 'randomized reduction lemma' to explain their time complexities in a simple and intuitive fashion.
This problem was featured 4 years later in BAPC ($$$n \leq 10,000$$$, same $$$a_i$$$ range, 12000 queries). You can solve it here: https://www.acmicpc.net/problem/26001