Как эффективно обрабатывать запросы вида "Найти сумму элементов, таких что x < a[i] < y на отрезке l < i < r" с изменением в элементе с помощью дерева отрезков?
→ Обратите внимание
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 164 |
| 1 | maomao90 | 164 |
| 3 | Um_nik | 163 |
| 4 | atcoder_official | 160 |
| 4 | adamant | 160 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 8 | Dominater069 | 154 |
| 8 | nor | 154 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 14.11.2024 19:47:34 (l3).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











ну когда ты строишь дерево отрезков , в функции build там где l==r проверяй если число соответствует твоему условию то t[v]=a[l]; а если нет то t[v]=0;
3d Mo
Пусть для каждой вершины дерева отрезков мы храним весь ее подотрезок в двоичном сбалансированном дереве (например, в декартовом дереве). Понятно, что для изменения в элементе небодимо обновить этот элемент в отрезках. Теперь рассмотрим запрос суммы. Понятно, что весь отрезок запроса мы можем разбить на
отрезках. Теперь рассмотрим запрос суммы. Понятно, что весь отрезок запроса мы можем разбить на  отрезков, которые есть в дереве отрезков. Теперь для каждого такого отрезка нам необходимо найти сумму всех элементов, для которых верно x < ai < y. Это легко сделать с помощью двоичного сбалансиванного дерева (дополнительно храним и обновляем сумму на поддереве), в котором хранится весь этот отрезок.
отрезков, которые есть в дереве отрезков. Теперь для каждого такого отрезка нам необходимо найти сумму всех элементов, для которых верно x < ai < y. Это легко сделать с помощью двоичного сбалансиванного дерева (дополнительно храним и обновляем сумму на поддереве), в котором хранится весь этот отрезок.
Итого получаем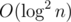 на запрос и
на запрос и 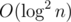 на обновление элемента.
на обновление элемента.
Если запросы даны offline, то можно для каждой вершины дерева отрезка найти все значения, которые там будут в какой-либо момент, и сжать их (для каждой вершины свое сжатие). После этого мы можем использовать более "статическую" структуру, например, дерево Фенвика. Запрос будет тоже за O(log2n), но вроде константа бинпоиска (сжатие) + Фенвика меньше, чем у декартова дерева.
Хорошее замечание :)
В некоторых задачах, например, 785E - Антон и перестановка, без этого довольно сложно поместиться в ограничения по времени.