CodeChef invites you to participate in the December CookOff 2012 at http://www.codechef.com/COOK29.
Time: 23rd December 2012 (2130 hrs) to 24th December 2012 (0000 hrs). (Indian Standard Time — +5:30 GMT) — Check your timezone.
Details: http://www.codechef.com/COOK29/
Registration: Just need to have a CodeChef user id to participate. New users please register here
Problem Setter: David Stolp
Problem Tester: Anton Lunyov
Editorialist: Pradeep Mathias
It promises to deliver on an interesting set of algorithmic problems with something for all.
The contest is open for all and those, who are interested, are requested to have a CodeChef userid, in order to participate.











"2130 hrs" is more than 88 days! I hope this is a typo! :D
2130 Hrs IST => 9:30 PM IST :P
Thank you for the contest! I liked the problemset very much.
Very interesting and balanced problemset! :)
Thanks for the nice contest. How many non-indian participants will receive Codechef T-Shirt?
Top 10 irrespective of nationality with get a goodie.
Oh, 5th problem! So simple solution! Really nice contest!
Finally, I've solved TREEROOT. Really nice constraints.
Thanks to David Stolp and Anton Lunyov for the great contest. The editorials will be available here: http://discuss.codechef.com/tags/cook29/
I bet you were thinking on a very hard way at first :)
Yes. Not only me, according to to comment's rating
А как дорешивать?
Скоро добавят. Вместо http://www.codechef.com/COOK29/problems/EXGCD по ссылке http://www.codechef.com/problems/EXGCD
Спасибо. Именно EXGCD и хочу допихать...
Там задачи высыпаются в раздел "Practice" согласно их сложности (по мнению авторов) почти сразу после контеста. Перебор + (ctrl + F) — единственный выход.
Edit: Tutorial is now available!
Can someone explain the idea behind "Expected Greatest Common Divisor". Looks like the editorial for this problem is a bit delayed.
I couldn't find a solution to the main problem: what is the number of 5-tuples (x1,...,x5) s.t. ai<=xi<=bi and gcd(x1,...,x5)=1. There was a simpler problem discussed on TopCoder forums, where the constraint was 1<=xi<=n.
Instead of directly answering your question, the solution (at least mine) first calculates the number of tuples where each element (and therefore GCD) is divisible by 1, 2, 3, ..., N = 200 000.
After that, the number of tuples with GCD being exactly 1, 2, 3, ..., N can be found in an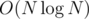 pass.
pass.
Thanks a lot for your answer. I did the 1st step of your comment, however I assumed the 2nd step would take O(N*N) time (till I saw your code :) ).