Editorial — Mathmania, Codefest' 18

№	Пользователь	Рейтинг
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

№	Пользователь	Вклад
1	cry	164
1	maomao90	164
3	Um_nik	163
4	atcoder_official	160
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
8	Dominater069	154
8	nor	154

Shooting Game

Let P_A and P_B be the probability of Alice and Bob hitting the target respectively. Then the chances of Alice winning the game are:

P_A + (1 - P_A)(1 - P_B)P_A + (1 - P_A)²(1 - P_B)²P_A + ...

which equals 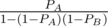$\text{[math]}$ using GP formula. Similarly, for Bob it would be $\text{[math]}$ .

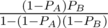Equating both we get, 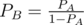$\text{[math]}$ . Return -1 in case you get P_B greater than 1.

SolveForTrisha

Let x be an n^th root of unity. Then, xⁿ = 1. So, xⁿ - 1 = 0 has roots 1, α₁, α₂....α_n - 1. We can write this as follows :

$\text{[math]}$

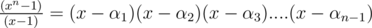
Placing x = 1, - 1 in the above equation and multiplying them, one can get the desired result.
If n is even the expression evaluates to 0 otherwise n.

Polynomial Guess

Consider the polynomial:

f(x) = x(x - 1)(x - 2)(x - 3)(x - 4)(x - 5)

Let g(r) be the value of 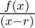$\text{[math]}$ at x = r and y(r) be the given values of the polynomial for r = 0 to 5.

The desired polynomial can be written as :

$\text{[math]}$ Placing x = 6 in above equation, the desired result can be obtained.

Code

#include <bits/stdc++.h>

#define ll          long long
#define pb          push_back
#define pii         pair<int,int>
#define vi          vector<int>
#define vii         vector<pii>
#define mi          map<int,int>
#define mii         map<pii,int>
#define all(a)      (a).begin(),(a).end()
#define x           first
#define y           second
#define sz(x)       (int)x.size()
#define endl        '\n'
#define hell        1000000007
#define rep(i,a,b)  for(int i=a;i<b;i++)
using namespace std;

class PolynomialGuess{
public:
	int findValue(int[] p) {
		return -p[0]+6*p[1]-15*p[2]+20*p[3]-15*p[4]+6*p[5];
	}
};

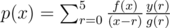
FunctionGame

The main part of the solution here is using the equation : φ(x^r) = x^r - 1φ(x) , 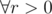$\text{[math]}$ . Rest is just solving GP sums and calculating φ values from 1 to m.

Code

#include <bits/stdc++.h>

#define ll          long long
#define pb          push_back
#define pii         pair<int,int>
#define vi          vector<int>
#define vii         vector<pii>
#define mi          map<int,int>
#define mii         map<int,pii>
#define all(a)      (a).begin(),(a).end()
#define x           first
#define y           second
#define sz(x)       (int)x.size()
#define hell        1000000007
#define endl        '\n'
#define rep(i,a,b)  for(int i=a;i<b;i++)
using namespace std;
ll phi[1000006];
int expo(int base,int exponent,int mod){
    int ans=1;
    while(exponent!=0){
        if(exponent&1) ans=(1LL*ans*base)%mod;
        base=(1LL*base*base)%mod;
        exponent>>=1;
    }
    return ans%mod;
}
void computeTotient(int n){
	for (int i=1; i<=n; i++)
        phi[i] = i;
    for (int p=2; p<=n; p++){
    	if (phi[p] == p){
    		phi[p] = p-1;
    		for (int i = 2*p; i<=n; i += p)
    			phi[i] = (phi[i]/p) * (p-1);
    	}
    }
}
class FunctionGame{
	public:
	int findValue(int m,int n){
		computeTotient(1e6);
		ll ans=n;
		rep(i,2,m+1){
			ans=ans+phi[i]*((((expo(i,n,hell)+hell-1)%hell)*expo(i-1,hell-2,hell))%hell);
			ans%=hell;
		}
		return ans;
	}
};

PrimeMaker

Since, the operations allowed are only modifying / deleting a digit and value of n is at max 10⁶, the maximum number that can be formed is of the rage 10n. The idea is to calculate all primes upto 10⁷ and take the minimum number of operations required to convert n to a prime p over all primes p.

Another solution is to observe that we can always get a prime number in the range n - 99 to n + 99 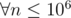$\text{[math]}$ . So, the maximum value of the answer can be 2 only. So, we just need to check whether the answer is 0 or 1. For answer to be 0, n should be prime. For answer to be 1 we have O(10 * d) candidates only where d is the number of digits in decimal representation of n. Each candidate can be checked in O(sqrt(n)).

Code

#include <bits/stdc++.h>

#define ll          long long
#define pb          push_back
#define pii         pair<int,int>
#define vi          vector<int>
#define vii         vector<pii>
#define mi          map<int,int>
#define mii         map<pii,int>
#define all(a)      (a).begin(),(a).end()
#define x           first
#define y           second
#define sz(x)       (int)x.size()
#define endl        '\n'
#define hell        1000000007
#define rep(i,a,b)  for(int i=a;i<b;i++)
using namespace std;

bool p[10000002];
vi primes;
void process_seive(int n){
    memset(p,1,sizeof p);
    rep(i,2,n+1){
        if(p[i]==0) continue;
        primes.pb(i);
        for(int j=2*i;j<=n;j+=i){
            p[j]=0;
        }
    }
}
int dp[10][10];
string s,prime;
int edit_distance(int x,int y){
    if(x==sz(s) and y==sz(prime)) return 0;
    if(dp[x][y]!=-1) return dp[x][y];
    int ans=hell;
    if(x<sz(s) and y<sz(prime)) ans=min(ans,edit_distance(x+1,y+1)+(s[x]!=prime[y]));
    if(x<sz(s)) ans=min(ans,edit_distance(x+1,y)+1);
    return dp[x][y]=ans;
}
class PrimeMaker{
public:
    int minimalOperation(int n){
        process_seive(10000000);
        s=to_string(n);
        int ans=hell;
        for(auto i:primes){
            prime=to_string(i);
            if(sz(prime)>sz(s)) break;
            memset(dp,-1,sizeof dp);
            ans=min(ans,edit_distance(0,0));
        }
        return ans;
    }
};

CountingTriangles

Let us try to find a series for the number of triangles after n steps. First of all the side length of the triangle after n steps would be m = 2ⁿ. Lets iterate over the side length of the triangles that we are going to count currently. Let it be l. Every triangle is either pointing up or pointing down. Lets count them separately and add them in the end. For counting triangles of length l pointing up, we just need to count the number of valid points that can be the topmost point of our triangle. This is equal to 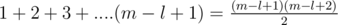$\text{[math]}$ . For counting triangles pointing down, we need to count the valid positions for placing the base of length l. This is equal to 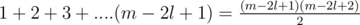$\text{[math]}$ . The final answer would be :

$\text{[math]}$ .
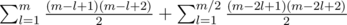Simplifying and using some series formulas, you can get a formula as : $\text{[math]}$ .
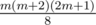If you do not want to solve the series, observe that the final expression would be of order 3 in m. So, instead assume a general 3 degree polynomial, and get its coefficients using base cases already given.

ConfusingTriangle

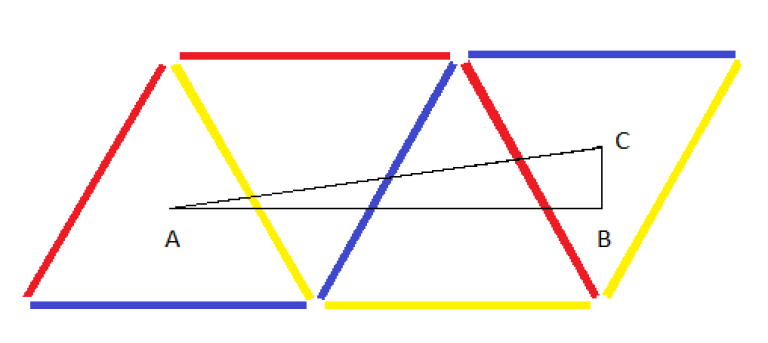
The idea here is to use the mirror property. Imagine that the sides of the triangles have mirrors placed on them. Then the shortest distance between two centroids such that the line between them intersects all the sides exactly once is your answer. Applying pythagoras theorum, the answer comes to be 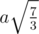$\text{[math]}$

MinimizeExpression

The key to the solution is to use Weighted AM — GM inequality here. Let us write the expression as

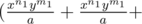$\text{[math]}$ . . . . a times 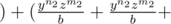$\text{[math]}$ . . . . b times 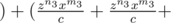$\text{[math]}$ . . . c times )

$\text{[math]}$

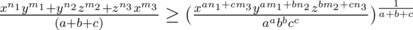
Comparing the RHS of the expression with x^Ay^Bz^C, solve for a, b and c. The final answer hence would be 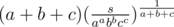$\text{[math]}$ .
The conditions given guarantee that a, b and c after solving would be positive.

Code

#include <bits/stdc++.h>

#define ll          long long
#define pb          push_back
#define pii         pair<int,int>
#define vi          vector<int>
#define vii         vector<pii>
#define mi          map<int,int>
#define mii         map<pii,int>
#define all(a)      (a).begin(),(a).end()
#define x           first
#define y           second
#define sz(x)       (int)x.size()
#define endl        '\n'
#define hell        1000000007
#define rep(i,a,b)  for(int i=a;i<b;i++)
using namespace std;

class MinimizeExpression{
public:
double findMinimum(int n1, int n2, int n3, int m1, int m2, int m3, int a, int b, int c, long long s){
        long double denom=m1*m2*m3+n1*n2*n3;
        long double x=(a*n2*n3+b*m2*m3-c*m3*n2)/denom;
        long double y=(-a*m1*n3+b*n1*n3+c*m1*m3)/denom;
        long double z=(a*m1*m2-b*m2*n1+c*n1*n2)/denom;
        long double ans=(x+y+z);
        long double temp=pow(x,x)*pow(y,y)*pow(z,z);
        temp=s/temp;
        temp=pow(temp,1.0l/(x+y+z));
        ans*=temp;
        return ans;
    }
};

EquationSolver

The answer to the problem is the coefficient of x^c in the expansion of :

(1 + x + x⁴ + x⁹ + .....)ⁿ

where (1 + x + x⁴ + x⁹ + .....) represents the choices each variable has.
One solution is to perform binary exponentiation of the polynomial using NTT for polynomial multiplication. The time complexity of such a solution would be O(clog(c)log(n)).
Another solution is to calculate NTT of the polynomial once, exponentiate individual terms to n and then calculate the inverse NTT. Time complexity of the solution would be O(c(log(c) + log(n))).

Code: 1st solution

#include <bits/stdc++.h>

#define int         long long
#define pb          push_back
#define pii         pair<int,int>
#define vi          vector<int>
#define vii         vector<pii>
#define mi          map<int,int>
#define mii         map<pii,int>
#define all(a)      (a).begin(),(a).end()
#define x           first
#define y           second
#define sz(x)       (int)x.size()
#define endl        '\n'
#define hell        998244353
#define rep(i,a,b)  for(int i=a;i<b;i++)
using namespace std;
int expo(int base,int exponent,int mod){
    int ans=1;
    while(exponent!=0){
        if(exponent&1) ans=(1LL*ans*base)%mod;
        base=(1LL*base*base)%mod;
        exponent>>=1;
    }
    return ans%mod;
}
const int mod=998244353;    
const int root=565042129;   // nth root of mod
const int root_1=950391366; // inverse of root
const int root_pw=1<<20;    // value of n
void fft(vi&a,bool invert){
    int i,j,n=(int)a.size();
    for(i=1,j=0;i<n;++i){
        int bit=n>>1;
        for(;j>=bit;bit>>=1){
            j-=bit;
        }
        j+=bit;
        if(i<j) swap(a[i],a[j]);
    }
    for(int len=2;len<=n;len<<=1){
        int wlen=invert?root_1:root;
        for(i=len;i<root_pw;i<<=1){
            wlen=(wlen*wlen%hell);
        }
        for(i=0;i<n;i+=len){
            int w=1;
            for(j=0;j<len/2;++j){
                int u=a[i+j],v=(int)(a[i+j+len/2]*w%hell);
                a[i+j]=(u+v+hell)%hell;
                a[i+j+len/2]=(u-v+hell)%hell;
                w=(w*wlen%hell);
            }
        }
    }
    if(invert){
        int nrev=expo(n,hell-2,hell);
        for(i=0;i<n;++i){
            a[i]=(a[i]*nrev%hell);
        }
    }
}
void multiply(const vi &a,const vi &b,vi &res){
    vi fa(a.begin(),a.end()),fb(b.begin(),b.end());
    size_t n=1;
    while(n<max(a.size(),b.size())) n<<=1;
    n<<= 1;
    fa.resize(n),fb.resize(n);
    fft(fa,false),fft(fb,false);
    for(size_t i=0;i<n;++i){
        fa[i]*=fb[i];
    }
    fft(fa,true);
    res.resize(n);
    for(size_t i=0;i<n;++i){
        res[i]=fa[i];
    }
}
vi cur,res;
void solve(){
    int n,c;
    cin>>n>>c;
    rep(i,0,c+1){
        int d=sqrt(i);
        if(d*d==i) cur.pb(1);
        else cur.pb(0);
    }
    res.pb(1);
    while(n){
        if(n&1){
            vi a=cur;
            vi b=res;
            multiply(a,b,res);
        }
        vi a=cur;
        vi b=cur;
        multiply(a,b,cur);
        n/=2;
    }
    cout<<res[c]<<endl;
}

signed main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    // cin>>t;
    while(t--){
        solve();
    }
    return 0;
}

Code: 2nd solution

#include <bits/stdc++.h>

#define int         long long
#define pb          push_back
#define pii         pair<int,int>
#define vi          vector<int>
#define vii         vector<pii>
#define mi          map<int,int>
#define mii         map<pii,int>
#define all(a)      (a).begin(),(a).end()
#define x           first
#define y           second
#define sz(x)       (int)x.size()
#define endl        '\n'
#define hell        998244353
#define rep(i,a,b)  for(int i=a;i<b;i++)
using namespace std;
int expo(int base,int exponent,int mod){
    int ans=1;
    while(exponent!=0){
        if(exponent&1) ans=(1LL*ans*base)%mod;
        base=(1LL*base*base)%mod;
        exponent>>=1;
    }
    return ans%mod;
}
const int mod=998244353;    
const int root=565042129;   // nth root of mod
const int root_1=950391366; // inverse of root
const int root_pw=1<<20;    // value of n
void fft(vi &a,bool invert){
    int i,j,n=(int)a.size();
    for(i=1,j=0;i<n;++i){
        int bit=n>>1;
        for(;j>=bit;bit>>=1){
            j-=bit;
        }
        j+=bit;
        if(i<j) swap(a[i],a[j]);
    }
    for(int len=2;len<=n;len<<=1){
        int wlen=invert?root_1:root;
        for(i=len;i<root_pw;i<<=1){
            wlen=(wlen*wlen%hell);
        }
        for(i=0;i<n;i+=len){
            int w=1;
            for(j=0;j<len/2;++j){
                int u=a[i+j],v=(int)(a[i+j+len/2]*w%hell);
                a[i+j]=(u+v+hell)%hell;
                a[i+j+len/2]=(u-v+hell)%hell;
                w=(w*wlen%hell);
            }
        }
    }
    if(invert){
        int nrev=expo(n,hell-2,hell);
        for(i=0;i<n;++i){
            a[i]=(a[i]*nrev%hell);
        }
    }
}
void solve(){
	vi cur;
    int n,c;
    cin>>n>>c;
    cur.resize(1<<20);
    for(int i=0;i*i<=c;++i) cur[i*i]=1;
    fft(cur,false);
    for(auto &i: cur) i=expo(i,n,hell);
	fft(cur,true);    
    cout<<cur[c]<<endl;
}

signed main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    // cin>>t;
    while(t--){
        solve();
    }
    return 0;
}

Tribonacci

T(n) = Mⁿ where M is the given matrix.

$\text{[math]}$

$\text{[math]}$ $\text{[math]}$

$\text{[math]}$ $\text{[math]}$

$\text{[math]}$ $\text{[math]}$

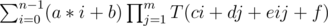
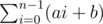
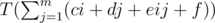
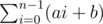
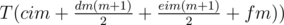
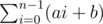
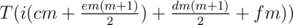
Let 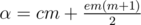$\text{[math]}$ and $\text{[math]}$ .

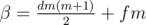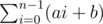$\text{[math]}$ T(αi + β)

Let R(n) = T(α)ⁿ

$\text{[math]}$

$\text{[math]}$

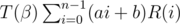
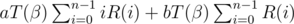
The main part of the solution is to calculate 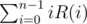$\text{[math]}$ and $\text{[math]}$ .
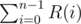Consider the following matrix P(A)
\begin{bmatrix} A & I \\ O & I \end{bmatrix} The matrices P², P³ . . . are as follows :
\begin{bmatrix} A^{2} & A+I \\ O & I \end{bmatrix}

\begin{bmatrix} A^{3} & A^{2}+A+I \\ O & I \end{bmatrix} Observe that the 2^nd element of the first row is the GP sum of matrix A. Therefore, 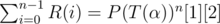$\text{[math]}$

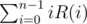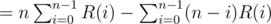
Now, consider $\text{[math]}$ .

$\text{[math]}$

The first part of which we already know. For second part, Consider 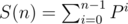$\text{[math]}$
The matrices S(2), S(3) . . . are as follows :
\begin{bmatrix} A^{2} & A+2I \\ O & I \end{bmatrix}

\begin{bmatrix} A^{3} & A^{2}+2A+3I \\ O & I \end{bmatrix} Observe that the second element of the first row is nothing but the desired part. S(n) can also be calculated in the same way the GP sum was calculated as it is nothing but another GP in P. The overall time complexity of the solution is O(k³(log(n) + log(m))).

Also observe that the modulus is 2³¹, so no need to take modulus. We can let the operations overflow. In the end we just add 2³¹ if result comes out to be negative.
Another method of taking modulus is to take bitwise AND of the intermediate calculations with 2³¹ - 1. Both of them are much faster than the modulo operation.

Code

#include <bits/stdc++.h>

#define ll          long long
#define pb          push_back
#define pii         pair<int,int>
#define vi          vector< int>
#define vii         vector<pii>
#define mi          map<int,int>
#define mii         map<pii,int>
#define all(a)      (a).begin(),(a).end()
#define x           first
#define y           second
#define sz(x)       (int)x.size()
#define endl        '\n'
#define hell        (1LL<<31)
#define rep(i,a,b)  for( int i=a;i<b;i++)
using namespace std;
class matrix{
public:
     int n;
    vector<vi> val;
    matrix( int n=2);
    matrix operator+(const matrix&) const;
    matrix operator-(const matrix&) const;
    matrix operator*(const matrix&) const;
    matrix& operator=(const matrix& b){
        val=b.val;
        n=b.n;
        return *this;
    }
    void set( int x){
        rep(i,0,n){
            rep(j,0,n){
                val[i][j]=x;
            }
        }
    }
    void print(){
        rep(i,0,n){
            rep(j,0,n){
                cout<<val[i][j]<<" ";
            }
            cout<<endl;
        }
    }
    matrix mul( int a){
        matrix ans(this->n);
        rep(i,0,this->n){
            rep(j,0,this->n){
                ans.val[i][j]=a*this->val[i][j];
            }
        }
        return ans;
    }
};
matrix::matrix( int x){
    n=x;
    val.resize(x);
    rep(i,0,x){
        val[i].resize(x);
    }
}
matrix matrix::operator+(const matrix& b) const{
    matrix ans(b.n);
    rep(i,0,b.n){
        rep(j,0,b.n){
            ans.val[i][j]=this->val[i][j]+b.val[i][j];
        }
    }
    return ans;
}
matrix matrix::operator-(const matrix& b) const{
    matrix ans(b.n);
    rep(i,0,b.n){
        rep(j,0,b.n){
            ans.val[i][j]=this->val[i][j]-b.val[i][j];
        }
    }
    return ans;
}
matrix matrix::operator*(const matrix& b) const{
    matrix ans(b.n);
    rep(i,0,b.n){
        rep(j,0,b.n){
            rep(k,0,b.n){
                ans.val[i][j]+=this->val[i][k]*b.val[k][j];
            }
        }
    }
    return ans;         
}
matrix identity( int N=2){
    matrix ans(N);
    rep(i,0,N){
        ans.val[i][i]=1;
    }
    return ans;
}
matrix matexpo(matrix a, ll n){
    if(n==0){
        return identity(a.n);
    }
    if(n==1) return a;
    matrix x=matexpo(a,n/2);
    matrix r=x*x;
    if(n&1) r=r*a;
    return r;
}
matrix transform(matrix R){
    matrix T(2*R.n);
    rep(i,0,2*R.n){
        rep(j,0,2*R.n){
            if(i<R.n and j<R.n){
                T.val[i][j]=R.val[i][j];
            }
            else if(i<R.n){
                T.val[i][j]=(i==j-R.n);
            }
            else if(j>=R.n){
                T.val[i][j]=(i==j);
            }
        }
    }
    return T;
}

class Tribonacci{
public:
    int findValue(int a, int b, int c, int d, int e, int f, ll n, ll m, vi mat){
        int k=sqrt(sz(mat));
        matrix M(k);
        rep(i,0,k){
            rep(j,0,k){
                M.val[i][j]=mat[i*k+j];
            }
        }
        matrix M1=transform(matexpo(matexpo(M,c),m)*matexpo(matexpo(matexpo(M,e),(m%2?m:m/2)),m%2?(m+1)/2:(m+1)));
        matrix M2=transform(M1);
        M=matexpo(matexpo(M,f),m)*matexpo(matexpo(matexpo(M,d),(m%2?m:m/2)),m%2?(m+1)/2:(m+1));
        M1=matexpo(M1,n);
        M2=matexpo(M2,n);
        matrix M11(k),M22(k);
        rep(i,0,k){
            rep(j,0,k){
                M11.val[i][j]=M1.val[i][j+k];
                M22.val[i][j]=M2.val[i][j+3*k];
            }
        }
        matrix final=((M11.mul(n-1)-M22)*M).mul(a)+(M*M11).mul(b);
         int res=0;
        rep(i,0,k){
            rep(j,0,k){
                res+=final.val[i][j];
            }
        }
        if(res<0) res+=hell;
        return res;
    }
};

Комментарии (9)

Показать архивные | Написать комментарий?

hitman623

6 лет назад, # |

Auto comment: topic has been updated by hitman623 (previous revision, new revision, compare).

→ Ответить

dragoon

How do you "Comparing the RHS of the expression with ..." in MinimizeExpression?

6 лет назад, # ^ |

← Rev. 3 →

The goal here is to choose such a, b, c (a, b, c > 0) such that the RHS of the expression in the inequality comes to be a function of x^Ay^Bz^C. For example : given xy² = 4, to minimize x + y you write it as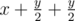 $\text{[math]}$ so that you get xy² on RHS.

← Rev. 2 →

No, I mean, how to relate the right hand side x^(an1+cm3).. with x^ay^bz^c=s? Or to put it the other way, why should we assume that is s?

Comparing them, you get the following :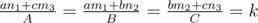 $\text{[math]}$ .

You are free to choose any k > 0 and solve for a, b, c. The answer is same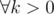 $\text{[math]}$ .

MazzForces

+20

how to upsolve ? can you move them to practice

I have contacted hmehta. I'll let you know as soon as he replies.

hmehta

The match is up in the practice rooms.

You will find it in SRMs Category under practice rooms as shown below in the image! :)

Setup Topcoder Java Applet: topcodr.co/SRMGuide

SevenDusks

2 года назад, # |

+13

There is something wrong in problem EquationSolver.

The standard solution is based on "calculate NTT of the polynomial once, exponentiate individual terms to n and then calculate the inverse NTT." which is wrong.

Because NTT does the Circular convolution.When you do this process NTT with length $$$2^i$$$,the result polynomial $$$F$$$ is not the answer. If we claim the correct polynomial as $$$G$$$.And $$$F$$$ will be $$$(G \bmod x^{2^i})$$$.

If you want to make it correct,you should do NTT with length $$$2^k$$$ which satisfies $$$2^k>n\times c$$$.But it's impossible with $$$998244353$$$ and time limit.

The correct algorithm is just do the ln transform,and multiply each terms with constant c,then do the exp transform.This works in $$$O(n\log n)$$$.For more details,please check this.

Блог пользователя hitman623

Shooting Game

SolveForTrisha

Polynomial Guess

FunctionGame

PrimeMaker

CountingTriangles

ConfusingTriangle

MinimizeExpression

EquationSolver

Tribonacci