I read the approach for finding Range minimum value using 2 Binary Indexed Trees. Is it possible to do this problem using only one BIT when updates are also there?
→ Обратите внимание
До соревнования
Rayan Programming Contest 2024 - Selection (Codeforces Round 989, Div. 1 + Div. 2)
3 дня
Зарегистрироваться »
Rayan Programming Contest 2024 - Selection (Codeforces Round 989, Div. 1 + Div. 2)
3 дня
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 155 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | nor | 152 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 27.11.2024 06:44:46 (j3).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











No, a normal BIT is only able to answer prefix RMQs. A BIT doesn't have enough information to answer a general RMQ (as it doesn't even store the value of each element).
You sure?
I have read this paper previously .In this paper two BITs have been used . I want to know if we can achieve the same result using a single BIT.
Found one approach for solving RMQ using BIT(without updates). Suppose our query range is [L,R]. We know that BIT[i] stores the result from index [i-(i & (-i))+1] to index i.
So for given query we start from R. Now first we check if index [R-(R & (-R))+1]>=L or not. if yes we just update the minimum value using the value in BIT[R] and update R by subtracting (R & (-R)) from R . if not then we just take minimum of A[R] and current answer and update R to R-1.
We keep on doing this while(R>=L).
This algorithm will return the correct result but cost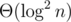 time complexity if you query the range [2, n].
time complexity if you query the range [2, n].
Can you provide some explanation for this complexity. Not able to get it.
Firstly R will go to the biggest 2k satisfying 2k ≤ n, then the progress will be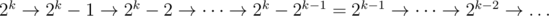 , between the progress
, between the progress  it would take k times. So the total time complexity is Θ(k2).
it would take k times. So the total time complexity is Θ(k2).