Для каждого x от 1 до 5000 заведем список таких индексов i что ai = x. Проверим, что во всех списках четное количество элементов и выведем содержимое списков парами.
Для каждой олимпиады пробежим по всему периоду ее подготовки. Для этого нужно научиться по текущей дате получать предыдущую. Для каждого из дней подготовки увеличим на pi количество различных членов жюри, которые должны работать в этот день. Тогда ответом на задачу будет максимальное из таких накопленных значений по всем дням. Не забудьте про 2012й год.
Обозначим количество символов x в строке s через Cs(x), а в строке t — через Ct(x). Тогда минимальное количество замен для получения анаграммы t из s есть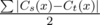 
. Теперь жадно построим лексикографически наименьшее решение. Будет идти в порядке возрастания позиции подбирать, какой символ будет в этой позиции в ответе. Найдем первый в порядке возрастания символ, которые может стоять на этом месте в оптимальном ответе. Для того, чтобы быстро проверять, может ли символ стоять или нет, мы будем все время пересчитывать величины Cs(x) и Ct(x) и вычислять, сколько необходимо замен по приведенной выше формуле.
Выберем произвольную клетку с крысой (например, верхнюю левую). Мы должны ее очистить. Сделаем из нее BFS, который не ходит на расстояние, большее d (назовем такой поиск в ширину d-BFS). Он посетит около 2d2 в худшем случае. Мы должны взорвать первую гранату в одной из этих клеток. Переберем все варианты. Сделаем d-BFS из клетки-кандидата. Некоторые клетки с крысами не будут очищены взрывом и, соответственно, не будут посещены обходом. Значит, они должны быть очищены взрывом второй гранаты. Выберем произвольную клетку с крысой, которая не была очищена. Сделаем из нее d-BFS. Все посещенные клетки — это кандидаты на место подрыва второй гранаты. Проверим их все. Для проверки опять же запустим d-BFS. Если он посетил все клетки, не очищенные взрывом первой гранаты, то мы нашли решение.
Каждый d-BFS посещает не более 2d2 клеток, поэтому общее число шагов будет около 8d6.
Задача может быть решена динамическим программированием: пусть D(n, r) — максимальный рейтинг, которого Вася сможет достичь за первые n дней при условии, что со дня с номером n осталось ровно r килограмм еды. Подумаем теперь, кого Васе кормить в следующий день. Очевидно, что если он решит покормить k друзей, то ему выгодней покормить первый k друзей с наименьшей прожорливостью в этот день. Переберем все возможные k и сделаем соответствующие переходы. Всего получается 4002 и 4003 переходов.
Скажите, а зачем было давать в задаче A ограничение 3*10^5 да ещё и тл 1сек? Неужели нельзя было просто 10^5? Это и систесты замедляет, и кажется может свалить адекватные решения просто из-за непродуманного ввода. Тем не менее в обоих случаях сам алгоритм одинаковый. Непонятно кого вы хотели поломать на этом.
Мое решение вообще прошло претесты во время контеста, а сейчас на систестах свалилось на претесте же. http://codeforces.me/blog/entry/6062#comment-114691
тоже самое еще у 3х человек, сабмитивших на Java6.
http://codeforces.me/contest/254/submission/2735059 http://codeforces.me/contest/254/submission/2735121 http://codeforces.me/contest/254/submission/2735754
и наверняка еще будет у кого-то. тупо.
А вот вообще лол: http://codeforces.me/contest/254/submission/2735486 . Памяти 0КБ, ога :)
UPD. Эх, оказывается я не один такой :(
http://codeforces.me/contest/254/submission/2734441 http://codeforces.me/contest/254/submission/2741882
find 1 difference=)
lucky
no=) vice versa.
9th test was pretest, firstly pretest got ac, but after contest it got tle. I could easily optimise it a bit on contest to get 100% AC, but it didn't fails from the beginning.
I think problem is in String.split because my solution got AC 781 ms.
it is not the big problem, i think.
http://codeforces.me/contest/254/submission/2742493 — just initializing vector with 5001 element give stable ac=)
http://codeforces.me/contest/254/submission/2742524 — or using ArrayList, like you.
and println(str + " " + str) not fast
yes, i know it, i just didn't care about it, because got ac on pretests=)
I had problem like u :|
Задача D.
Как, после первого шага, быстро найти первую, не убитую крысу? А после второго, как понять, всех ли мы убили?
так как площадь двух областей взрыва не более 2 * (d2 + (d + 1)2) = 290, а значит крыс тоже не больше, то можно и в тупую посмотреть
просто влоб, бежим по всем крысам, мы пройдем максимум 2d2 крыс, т.к. после первого шага максимум столько клеток посещено, а после второго тоже просто в лоб, т.к. мы два раза посетим 2d2 клеток, т.е. в принципе, если крыс больше, чем 4d2, то ответ -1.
Круто, спасибо. Просто где-нибудь в векторе сохранить их координаты, получается?
именно,
голубчикголубушкаНе читал разбор, я делал так: если крыс больше 290 то ответ -1 — мы не сможем убить больше при d<=8; находим две самые далёкие крысы (просто x*x+y*y), рассматриваем просто два квадрата со сторонами 2d+1 и центрами в найденных точках — это центры возможных взрывов, причём других центров быть не может. Ну а теперь нужно просто по найденным двум центрам проверить убивают ли они всех крыс — от каждого пускаем ширину и смотрим все ли крысы убились.
Задача 254C - Анаграмма вполне решается за линию без подбора, хотя и жадно асимптотика неплоха :)
I think that judging system didn't work properly during the contest. I got some TLE on test#9 for problem A, with my O(N) algorithm. after some TLE , I got AC with the same code :-?? it's funny that, at the final tests I got TLE on test#9 again :D and after the contest, that code got AC :-??
You got AC with 968/1000ms. It's OK, that execution time slightly changes. You have to write more fast code to be sure. +/- 50ms is quite little time.
BTW, your solution is too slow because you flush(use endl) too often. If you will use '\n' you'll get faster solution. (I was wrong, throught, it doesn't help a lot. GCC helps here, twice faster:) )
u'r right, tnx. but that's not fair, the test should be passed or not. my rank is badly decreased for this reason :((
so you should submit fast enough solution
we are awalys appreciate you .
Problem C reminds me with yesterday's SRM .. the Div1-250 pointer, but for sure it was with small constraints.
“For a fixed position, look through all characters from 'a' to 'z' and for each character decide whether the optimal answer can contain this character in that position.” How to decide whether the optimal answer can contain this character in that position or not?
problem C
Calculate the minimum number of changes that we will need if we place this character. Compare this number with the optimal answer.
Ok，thank you.I see.
There was some discussion in Russian about problem D, which I didn't quite understand (go figure!). There is an alternative solution, leading to the same running time.
Step 1 First check if the number of rats is > (d + d + 1)^2 + 1. If that is the case, return -1 immediately — there is no way how to blow the bombs as to cover more than this number. Actually, my solution fails because I didn't add 1 to the sum, i.e. off-by-one error :)
Step 2 For every rat, run a d-BFS to find the cells, where a bomb should be to kill it. As the rats are 4*d^2 and the d-BFS takes 2*d^2, this step takes approximately 6*d^4 operations. Sort the cells for convenience later, making it 4*d^2 * (2*d^2 * log(2*d^2)) = 16*d^4*log(d) (don't know why you are using operations insted of Big-O notation, but I'll stick with your way. I guess for a such a small d it kind of makes sense).
Step 3 Then, similar to your solution, do a single BFS from any rat (it should be covered by at least one bomb). Any of the covered cells is a candidate for the first bomb. Try all of them.
Step 4 For each of them, iterate through all rats. If the rat is covered by the bomb, skip it. As we have found the cells, covered by each rat in step 2, this can be done in O(log(d^2)) per rat. Otherwise, maintain a set of feasible cells, where the second bomb can be. That is just the intersection of the current set of feasible cells with the cells, possible for the current rat. As we have sorted the cells, this can be done linearly. 2*d^2 cells for the first bomb, 4*d^2 rats to check, each of them requiring 2*d^2 operations — 16*d^6. However, in practice it is much much faster, because the set intersection cannot contain always 2*d^2 cells — it actually reduces its size with d with each new rat.
Мое решение 2761184 по 254D - Крысы получает ТЛ63 , если начинать с верхней левой крысы, и ОК — если с нижней правой. Для хранения посещенных клеток использую сеты, что я делаю не так?
Вопрос по задаче E 155 контеста. Можно или нельзя задать начальные условия таким образом?
и если можно, то почему большинство найденных мною решений получивших AC не решают такой случай...
Да можно.
Can you please repair the system for this round: http://codeforces.me/contest/254/submission/3038666 (I have a similar one for prob A)
Anyone? Thanks
http://codeforces.me/contest/254/submission/21400911
Can someone help point out where did I messed up? I think my code should also work in O(d^6).