Автор: Михаил Мирзаянов (MikeMirzayanov).
Разбор
Tutorial is loading...
Решение
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n,k;
cin>>n>>k;
string s;
cin>>s;
sort(s.begin(),s.end());
char last='a'-2;
int ans=0;
int len=0;
for(int i=0;i<n;i++)
if(s[i]>=last+2)
{
last=s[i];
ans+=s[i]-'a'+1;
len++;
if(len>=k)
cout<<ans,exit(0);
}
cout<<-1;
}
1011B - Планировние экспедиции
Автор: Михаил Мирзаянов (MikeMirzayanov).
Разбор
Tutorial is loading...
Решение
#include <bits/stdc++.h>
using namespace std;
const int N = 100;
int main() {
int n, m;
cin >> n >> m;
vector<int> c(N + 1);
for (int i = 0; i < m; i++) {
int a;
cin >> a;
c[a]++;
}
for (int d = N; d >= 1; d--) {
vector<int> cc(c);
int k = 0;
for (int i = 1; i <= N; i++)
while (cc[i] >= d) {
k++;
cc[i] -= d;
}
if (k >= n) {
cout << d << endl;
return 0;
}
}
cout << 0 << endl;
}
Автор: Владислав Заводник (VladProg).
Разбор
Tutorial is loading...
Решение
#include<bits/stdc++.h>
using namespace std;
int main()
{
int n,m;
cin>>n>>m;
int a[n];
for(int i=0;i<n;i++)
{
cin>>a[i];
if(a[i]<=1)
{
printf("-1\n");
exit(0);
}
}
int b[n];
for(int i=0;i<n;i++)
{
cin>>b[i];
if(b[i]<=1)
{
printf("-1\n");
exit(0);
}
}
double s=m;
s+=s/(a[0]-1);
for(int i=n-1;i>=1;i--)
{
s+=s/(b[i]-1);
s+=s/(a[i]-1);
}
s+=s/(b[0]-1);
printf("%.10lf\n",s-m);
}
1011D - Ракета / 1010B - Ракета
Автор: Владислав Заводник (VladProg).
Разбор
Tutorial is loading...
Решение
#include <bits/stdc++.h>
using namespace std;
int query(int y)
{
cout<<y<<"\n";
fflush(stdout);
int t;
cin>>t;
if(t==0||t==-2)
exit(0);
return t;
}
int main()
{
int m,n;
cin>>m>>n;
int p[n];
for(int i=0;i<n;i++)
{
int t=query(1);
p[i]=t==1;
}
int l=2,r=m;
for(int q=0;;q++)
{
int y=(l+r)/2;
int t=query(y);
if(!p[q%n])
t*=-1;
if(t==1)
l=y+1;
else
r=y-1;
}
}
1011E - Граница / 1010C - Граница
Автор: Владислав Заводник (VladProg).
Разбор
Tutorial is loading...
Решение
#include<bits/stdc++.h>
using namespace std;
int gcd(int a,int b)
{
if(a<b)
swap(a,b);
return (b==0)?a:gcd(b,a%b);
}
int main()
{
int n,k;
scanf("%d%d",&n,&k);
int g=0;
for(int i=0;i<n;i++)
{
int t;
scanf("%d",&t);
g=gcd(g,t);
}
set<int> ans;
for(long long i=0,s=0;i<k;i++,s+=g)
ans.insert(s%k);
printf("%d\n",ans.size());
for(set<int>::iterator i=ans.begin();i!=ans.end();i++)
printf("%d ",*i);
}
1011F - Марсоход / 1010D - Марсоход
Автор: Владислав Заводник (VladProg).
Разбор
Tutorial is loading...
Решение
#pragma GCC optimize("O3")
#include<bits/stdc++.h>
using namespace std;
struct vertex
{
char type;
vector<int>in;
bool val;
bool change;
};
int n;
vector<vertex> g;
int dfs1(int v)
{
switch(g[v].type)
{
case 'A':
g[v].val = dfs1(g[v].in[0]) & dfs1(g[v].in[1]);
break;
case 'O':
g[v].val = dfs1(g[v].in[0]) | dfs1(g[v].in[1]);
break;
case 'X':
g[v].val = dfs1(g[v].in[0]) ^ dfs1(g[v].in[1]);
break;
case 'N':
g[v].val = ! dfs1(g[v].in[0]);
break;
}
return g[v].val;
}
void dfs2(int v)
{
if(g[v].change==false)
for(int i=0;i<g[v].in.size();i++)
g[g[v].in[i]].change=false;
else
switch(g[v].type)
{
case 'A':
if(g[v].val==(!g[g[v].in[0]].val&g[g[v].in[1]].val)) /// equal to if(g[g[v].in[1]].val==false)
g[g[v].in[0]].change=false;
else
g[g[v].in[0]].change=true;
if(g[v].val==(g[g[v].in[0]].val&!g[g[v].in[1]].val)) /// equal to if(g[g[v].in[0]].val==false)
g[g[v].in[1]].change=false;
else
g[g[v].in[1]].change=true;
break;
case 'O':
if(g[v].val==(!g[g[v].in[0]].val|g[g[v].in[1]].val)) /// equal to if(g[g[v].in[1]].val==true)
g[g[v].in[0]].change=false;
else
g[g[v].in[0]].change=true;
if(g[v].val==(g[g[v].in[0]].val|!g[g[v].in[1]].val)) /// equal to if(g[g[v].in[0]].val==true)
g[g[v].in[1]].change=false;
else
g[g[v].in[1]].change=true;
break;
case 'X':
if(g[v].val==(!g[g[v].in[0]].val^g[g[v].in[1]].val)) /// equal to if(false)
g[g[v].in[0]].change=false;
else
g[g[v].in[0]].change=true;
if(g[v].val==(g[g[v].in[0]].val^!g[g[v].in[1]].val)) /// equal to if(false)
g[g[v].in[1]].change=false;
else
g[g[v].in[1]].change=true;
break;
case 'N':
if(g[v].val==(!!g[g[v].in[0]].val)) /// equal to if(false)
g[g[v].in[0]].change=false;
else
g[g[v].in[0]].change=true;
break;
}
for(int i=0;i<g[v].in.size();i++)
dfs2(g[v].in[i]);
}
int main()
{
scanf("%d",&n);
g.resize(n);
for(int i=0;i<n;i++)
{
char c[4];
scanf("%s",c);
g[i].type=c[0];
int x;
switch(g[i].type)
{
case 'I':
scanf("%d",&x);
g[i].val=x;
break;
case 'N':
scanf("%d",&x);
g[i].in.push_back(x-1);
break;
default:
scanf("%d",&x);
g[i].in.push_back(x-1);
scanf("%d",&x);
g[i].in.push_back(x-1);
break;
}
}
dfs1(0);
g[0].change=true;
dfs2(0);
for(int i=0;i<n;i++)
if(g[i].type=='I')
printf("%d",g[0].val^g[i].change);
}
Автор: Владислав Заводник (VladProg).
Разбор
Tutorial is loading...
Решение
#include<bits/stdc++.h>
using namespace std;
int xmax,ymax,zmax,n,m,k;
map< int , map< int , pair< int ,int > > > pmap;
vector< pair< int , map< int , pair< int ,int > > > > pvector;
vector< pair< vector< pair< int , pair< int , int > > > , vector< pair< int , int > > > > tree;
int oxl,oxr,oyl,oyr,ozl,ozr;
pair<int,int> comb(pair<int,int> p1,pair<int,int> p2)
{
return make_pair(max(p1.first,p2.first),
min(p1.second,p2.second));
}
void build_y(int vx,int lxt, int rxt,int vy,int lyt, int ryt)
{
if(lyt==ryt)
{
if(lxt==rxt)
tree[vx].second[vy]=tree[vx].first[lyt].second;
else
{
int sl,sr;
sl=0,sr=tree[vx*2+1].first.size()-1;
while(sr>sl)
{
int sm=(sl+sr)/2;
if(tree[vx*2+1].first[sm].first>=tree[vx].first[lyt].first)
sr=sm;
else
sl=sm+1;
}
pair<int,int> res1=(tree[vx*2+1].first[sl].first==tree[vx].first[lyt].first)?
(tree[vx*2+1].first[sl].second):
make_pair(0,(int)zmax+1);
sl=0,sr=tree[vx*2+2].first.size()-1;
while(sr>sl)
{
int sm=(sl+sr)/2;
if(tree[vx*2+2].first[sm].first>=tree[vx].first[lyt].first)
sr=sm;
else
sl=sm+1;
}
pair<int,int> res2=(tree[vx*2+2].first[sl].first==tree[vx].first[lyt].first)?
(tree[vx*2+2].first[sl].second):
make_pair(0,(int)zmax+1);
tree[vx].second[vy]=comb(res1,res2);
}
}
else
{
int myt=(lyt+ryt)/2;
build_y(vx,lxt,rxt,vy*2+1,lyt,myt);
build_y(vx,lxt,rxt,vy*2+2,myt+1,ryt);
tree[vx].second[vy]=comb(tree[vx].second[vy*2+1],tree[vx].second[vy*2+2]);
}
}
void build_x(int vx,int lxt, int rxt)
{
if(lxt==rxt)
tree[vx].first=vector< pair< int , pair< int , int > > >(pvector[lxt].second.begin(),pvector[lxt].second.end());
else
{
int mxt=(lxt+rxt)/2;
build_x(2*vx+1,lxt,mxt);
build_x(2*vx+2,mxt+1,rxt);
for(vector< pair< int , pair< int , int > > >::iterator i=tree[2*vx+1].first.begin(),j=tree[2*vx+2].first.begin();;)
{
if(i==tree[2*vx+1].first.end())
{
for(;j!=tree[2*vx+2].first.end();j++)
tree[vx].first.push_back(*j);
break;
}
if(j==tree[2*vx+2].first.end())
{
for(;i!=tree[2*vx+1].first.end();i++)
tree[vx].first.push_back(*i);
break;
}
if(i->first<j->first)
{
tree[vx].first.push_back(*i);
i++;
}
else if(j->first<i->first)
{
tree[vx].first.push_back(*j);
j++;
}
else
{
tree[vx].first.push_back(make_pair(i->first,comb(i->second,j->second)));
i++;
j++;
}
}
}
tree[vx].second.resize(tree[vx].first.size()*4);
build_y(vx,lxt,rxt,0,0,tree[vx].first.size()-1);
}
pair<int,int> get_y(int vx, int vy, int lyt, int ryt, int lyc, int ryc)
{
if(lyc>ryc)
return make_pair(0,zmax+1);
if(lyc==lyt&&ryt==ryc)
return tree[vx].second[vy];
int myt=(lyt+ryt)/2;
return comb(get_y(vx,vy*2+1,lyt,myt,lyc,min(ryc,myt)),
get_y(vx,vy*2+2,myt+1,ryt,max(lyc,myt+1),ryc));
}
pair<int,int> get_x(int vx, int lxt, int rxt, int lxc, int rxc, int ly, int ry)
{
if(lxc>rxc)
return make_pair(0,zmax+1);
if(lxc==lxt&&rxt==rxc)
{
int sl,sr;
sl=0,sr=tree[vx].first.size()-1;
while(sr>sl)
{
int sm=(sl+sr)/2;
if(tree[vx].first[sm].first>=ly)
sr=sm;
else
sl=sm+1;
}
int lyc=sl;
sl=0,sr=tree[vx].first.size()-1;
while(sr>sl)
{
int sm=(sl+sr+1)/2;
if(tree[vx].first[sm].first<=ry)
sl=sm;
else
sr=sm-1;
}
int ryc=sr;
return (tree[vx].first[lyc].first>=ly&&tree[vx].first[ryc].first<=ry)?
get_y(vx,0,0,tree[vx].first.size()-1,lyc,ryc):
make_pair(0,(int)zmax+1);
}
int mxt=(lxt+rxt)/2;
return comb(get_x(vx*2+1,lxt,mxt,lxc,min(rxc,mxt),ly,ry),
get_x(vx*2+2,mxt+1,rxt,max(lxc,mxt+1),rxc,ly,ry));
}
int main()
{
scanf("%d%d%d%d%d%d",&xmax,&ymax,&zmax,&n,&m,&k);
oxl=xmax;
oxr=1;
oyl=ymax;
oyr=1;
ozl=zmax;
ozr=1;
for(int i=0;i<n;i++)
{
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
oxl=min(oxl,x);
oxr=max(oxr,x);
oyl=min(oyl,y);
oyr=max(oyr,y);
ozl=min(ozl,z);
ozr=max(ozr,z);
}
for(int i=0;i<m;i++)
{
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
if(oxl<=x&&x<=oxr&&oyl<=y&&y<=oyr&&ozl<=z&&z<=ozr)
{
printf("INCORRECT\n");
exit(0);
}
map< int , pair< int ,int > >::iterator it=pmap[x].insert(make_pair(y,make_pair(0,zmax+1))).first;
if(z<=ozr)
it->second.first=max(it->second.first,z);
if(z>=ozl)
it->second.second=min(it->second.second,z);
}
printf("CORRECT\n");
if(m>0)
{
pvector=vector< pair< int , map< int , pair< int ,int > > > >(pmap.begin(),pmap.end());
tree.resize(pvector.size()*4);
build_x(0,0,pvector.size()-1);
}
for(int i=0;i<k;i++)
{
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
if(oxl<=x&&x<=oxr&&oyl<=y&&y<=oyr&&ozl<=z&&z<=ozr)
{
printf("OPEN\n");
continue;
}
if(m==0)
{
printf("UNKNOWN\n");
continue;
}
bool closed=false;
for(int ii=0;ii<=1;ii++)
for(int jj=0;jj<=1;jj++)
{
if(closed)
break;
int i=oxl+ii*(oxr-oxl);
int j=oyl+jj*(oyr-oyl);
int lx=min(x,i),rx=max(x,i);
int sl,sr;
sl=0,sr=pvector.size()-1;
while(sr>sl)
{
int sm=(sl+sr)/2;
if(pvector[sm].first>=lx)
sr=sm;
else
sl=sm+1;
}
int lxc=sl;
sl=0,sr=pvector.size()-1;
while(sr>sl)
{
int sm=(sl+sr+1)/2;
if(pvector[sm].first<=rx)
sl=sm;
else
sr=sm-1;
}
int rxc=sr;
if(pvector[lxc].first>=lx&&pvector[rxc].first<=rx)
{
pair<int,int> p=get_x(0,0,pvector.size()-1,lxc,rxc,min(y,j),max(y,j));
if(min({z,ozl,ozr})<=p.first||max({z,ozl,ozr})>=p.second)
closed=true;
}
}
if(closed)
printf("CLOSED\n");
else
printf("UNKNOWN\n");
}
}
Авторы: Ильдар Гайнуллин (300iq) и Дмитрий Саютин (cdkrot).
Разбор
Tutorial is loading...
Решение
#include <cmath>
#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
#include <set>
#include <map>
#include <list>
#include <time.h>
#include <math.h>
#include <random>
#include <deque>
#include <queue>
#include <cassert>
#include <unordered_map>
#include <unordered_set>
#include <iomanip>
#include <bitset>
#include <sstream>
using namespace std;
typedef long long ll;
mt19937 rnd(228);
const int md = 998244353;
inline void add(int &a, int b) {
a += b;
if (a >= md) a -= md;
}
inline void sub(int &a, int b) {
a -= b;
if (a < 0) a += md;
}
inline int mul(int a, int b) {
#if !defined(_WIN32) || defined(_WIN64)
return (int) ((long long) a * b % md);
#endif
unsigned long long x = (long long) a * b;
unsigned xh = (unsigned) (x >> 32), xl = (unsigned) x, d, m;
asm(
"divl %4; \n\t"
: "=a" (d), "=d" (m)
: "d" (xh), "a" (xl), "r" (md)
);
return m;
}
inline int power(int a, long long b) {
int res = 1;
while (b > 0) {
if (b & 1) {
res = mul(res, a);
}
a = mul(a, a);
b >>= 1;
}
return res;
}
inline int inv(int a) {
a %= md;
if (a < 0) a += md;
int b = md, u = 0, v = 1;
while (a) {
int t = b / a;
b -= t * a; swap(a, b);
u -= t * v; swap(u, v);
}
assert(b == 1);
if (u < 0) u += md;
return u;
}
namespace ntt {
int base = 1;
vector<int> roots = {0, 1};
vector<int> rev = {0, 1};
int max_base = -1;
int root = -1;
void init() {
int tmp = md - 1;
max_base = 0;
while (tmp % 2 == 0) {
tmp /= 2;
max_base++;
}
root = 2;
while (true) {
if (power(root, 1 << max_base) == 1) {
if (power(root, 1 << (max_base - 1)) != 1) {
break;
}
}
root++;
}
}
void ensure_base(int nbase) {
if (max_base == -1) {
init();
}
if (nbase <= base) {
return;
}
assert(nbase <= max_base);
rev.resize(1 << nbase);
for (int i = 0; i < (1 << nbase); i++) {
rev[i] = (rev[i >> 1] >> 1) + ((i & 1) << (nbase - 1));
}
roots.resize(1 << nbase);
while (base < nbase) {
int z = power(root, 1 << (max_base - 1 - base));
for (int i = 1 << (base - 1); i < (1 << base); i++) {
roots[i << 1] = roots[i];
roots[(i << 1) + 1] = mul(roots[i], z);
}
base++;
}
}
void fft(vector<int> &a) {
int n = (int) a.size();
assert((n & (n - 1)) == 0);
int zeros = __builtin_ctz(n);
ensure_base(zeros);
int shift = base - zeros;
for (int i = 0; i < n; i++) {
if (i < (rev[i] >> shift)) {
swap(a[i], a[rev[i] >> shift]);
}
}
for (int k = 1; k < n; k <<= 1) {
for (int i = 0; i < n; i += 2 * k) {
for (int j = 0; j < k; j++) {
int x = a[i + j];
int y = mul(a[i + j + k], roots[j + k]);
a[i + j] = x + y - md;
if (a[i + j] < 0) a[i + j] += md;
a[i + j + k] = x - y + md;
if (a[i + j + k] >= md) a[i + j + k] -= md;
}
}
}
}
vector<int> multiply(vector<int> a, vector<int> b, int eq = 0) {
int need = (int) (a.size() + b.size() - 1);
int nbase = 0;
while ((1 << nbase) < need) nbase++;
ensure_base(nbase);
int sz = 1 << nbase;
a.resize(sz);
b.resize(sz);
fft(a);
if (eq) b = a; else fft(b);
int inv_sz = inv(sz);
for (int i = 0; i < sz; i++) {
a[i] = mul(mul(a[i], b[i]), inv_sz);
}
reverse(a.begin() + 1, a.end());
fft(a);
a.resize(need);
while (!a.empty() && a.back() == 0) {
a.pop_back();
}
return a;
}
vector<int> square(vector<int> a) {
return multiply(a, a, 1);
}
};
const int N = 1e5 + 1;
vector <vector <int> > polys[N];
int l[N], r[N];
int who[N];
int sz[N];
vector <int> slozh(const vector <int> &a, const vector <int> &b)
{
int n = (int) a.size(), m = (int) b.size();
vector <int> c(max(n, m));
for (int i = 0; i < n; i++) add(c[i], a[i]);
for (int i = 0; i < m; i++) add(c[i], b[i]);
return c;
}
pair <vector <int>, vector <int> > eval(const vector <vector <int> > &a)
{
if (a.size() == 1)
{
auto ret = a[0];
ret[0]++;
return {ret, a[0]};
}
else
{
int m = (int) a.size() / 2;
vector <vector <int> > l, r;
for (int i = 0; i < m; i++)
{
l.push_back(a[i]);
}
for (int i = m; i < (int) a.size(); i++)
{
r.push_back(a[i]);
}
auto lf = eval(l), rf = eval(r);
add(lf.first[0], -1);
auto P = slozh(ntt::multiply(lf.first, rf.second), rf.first);
auto Q = ntt::multiply(lf.second, rf.second);
return {P, Q};
}
}
vector <int> g[N];
void dfs(int v, int pr)
{
vector <int> go;
int deg = 0;
for (int to : g[v])
{
if (to != pr)
{
go.push_back(to);
deg++;
}
}
if (deg == 0)
{
polys[v].push_back({0, 1});
sz[v] = 1;
who[v] = v;
}
else
{
if (deg == 2)
{
l[v] = go[0];
r[v] = go[1];
dfs(l[v], v);
dfs(r[v], v);
sz[v] = sz[l[v]] + sz[r[v]] + 1;
if (sz[l[v]] < sz[r[v]])
{
swap(l[v], r[v]);
}
auto go = eval(polys[who[r[v]]]).first;
go.insert(go.begin(), 0);
polys[who[l[v]]].push_back(go);
who[v] = who[l[v]];
}
else
{
int son = go[0];
dfs(son, v);
sz[v] = sz[son] + 1;
who[v] = who[son];
polys[who[v]].push_back({0, 1});
}
}
}
vector <int> binom(ll n, int k)
{
if (n == 0)
{
vector <int> ret(k + 1);
ret[0] = 1;
return ret;
}
else if (n % 2 == 0)
{
auto a = binom(n / 2, k);
a = ntt::square(a);
a.resize(k + 1);
return a;
}
else
{
auto a = binom(n - 1, k);
for (int i = k; i >= 0; i--)
{
if (i != 0)
{
add(a[i], a[i - 1]);
}
}
return a;
}
}
int main()
{
#ifdef ONPC
freopen("a.in", "r", stdin);
#endif
ios::sync_with_stdio(0);
cin.tie(0);
int n;
cin >> n;
ll x;
cin >> x;
vector <int> fact(n + 1), rev_fact(n + 1);
fact[0] = 1;
for (int i = 1; i <= n; i++)
{
fact[i] = mul(fact[i - 1], i);
}
for (int i = 0; i <= n; i++)
{
rev_fact[i] = inv(fact[i]);
}
for (int i = 1; i < n; i++)
{
int a, b;
cin >> a >> b;
a--, b--;
g[a].push_back(b);
g[b].push_back(a);
}
dfs(0, -1);
auto solve = eval(polys[who[0]]).first;
auto big_binoms = binom(x, n);
for (int i = 0; i <= n; i++)
{
big_binoms[i] = mul(big_binoms[i], rev_fact[i]);
}
rev_fact.insert(rev_fact.begin(), 0);
big_binoms = ntt::multiply(big_binoms, rev_fact);
int ans = 0;
for (int i = 1; i <= n; i++)
{
add(ans, mul(mul(solve[i], big_binoms[i]), fact[i - 1]));
}
cout << ans << '\n';
}











For Rocket bonus, you can check 1 then 2 then 3 etc. while recording p[] values. When you want to search for the answer do not include already searched values. which will turn 1073741853 to 1073741823. which can be done with 30 iteration.
I guess that solution to F is exactly the same as my one from this comment: http://codeforces.me/blog/entry/60806#comment-447283, but here author is just collecting and keeping polynomials from heavy path.
Yup, it seems that my solution is exactly the same as yours :)
mlogm div2 B solution with data structures (probably not the mlogm the tutorial wants xD)
Instead of checking every time, we want to run a process that computes time.
Make an array of food sizes, where each number x means there are x packets of one food type.
Sort this array in decreasing order.
Now loop through the array, for each point we want to find the maximum arr[i]/(used[i]+1), and this value can be maintained by a segment tree (store arr[i], used[i] and merge two nodes based on arr[i]/(used[i]+1)). And we assign the person to such a food pile.
We loop through at max M elements, assign at max M people and we have a factor of logM from the segment tree, and we have another MlogM because sorting. It's overall O(M+MlogM+MlogM) = O(MlogM).
Another O(mlogm) solution is to binary search the answer with lower bound of 0 and upper bound of m.
Yeah that's what the tutorial wants, and what most people went for. I just decided to share some interesting alternative, even if not the best.
I think you just want to show everyone that you did a badass code with segment tree, so everyone should think that you were cool
that's because he is cool
Yeah, showing a solution with advance technique of an easy problem is cool
it's not about the post, it's about the poster
Yes, i talked about showing. So the post was showing, or the poster?
advanced*
Many participants have solution on div1E based on finding the number of points inside a box in 3D space. How to do this effectively?
Offline with scanline + 2d segment tree, for example
Could you please tell me if we can use three one-dimensional segment tree to solve Div1.E?
No I doesn't work like that, because for 3D segtree (which you almost always never need because you can remove a dimension with sweep or something) you are querying for three constraints.
So its something like Q(A and B and C) where A,B,C are [left,right] range query in some dimension.
But using three one dimension is like Q(A) + Q(B) + Q(C).
For div2 F, what I tried was merge all nots and mark it at some other operation node(with help of a xor store for each node). Now I believe the tree is complete binary tree . So if a leaf node is to be altered I can go down to that node and use the stored values in intermediatory nodes(as we do in a segment tree). The complexity for each such query would be O(log N) I think. So overall complexity should be : O(Nlog N). Even then my code gives TLE. Can someone point out if I am going wrong.
If I understand correctly, you think that tree depth can be maximum log(N). But it is wrong, because you can build edges only to the left or only to the right, so the depth will be N.
Thanks !!! I got it now . I hadn't thought properly the previous night . The depth goes order n in a simple test case of a n ordered bamboo of ANDs inclined left with each AND node having an IN node to right . Anyways thanks MaxZubec
The English is not very good. But thanks for the editorial, I managed to understand.
In problem E, we can eliminate another coordinate from the data structure by taking advantage of the fact that we can process queries offline, so we can sort them by 0-th coordinate. This results in a O(nlogn) solution that uses only simple 1D Fenwick tree with min operation as the data structure.
Not very readable code: http://codeforces.me/contest/1010/submission/40820468
I think that Div 1. E can be solved with a simple segment tree.
First, just as the tutorial says, we check the possibility of "INCORRECT". Then, each of the m moments can be treated as a open-ended 3D-box, i.e. denote the moment as (xi, yi, zi), if xi < xl, the restriction for knowing the moment (x, y, z) is "CLOSED" using this knowledge will be x ≤ xi, if xl ≤ xi ≤ xr, there will be no restriction for x, and if xi > xr, the restriction will be x ≥ xi. The same goes for yi and zi. Putting the 3 restrictions together gives you a open-ended 3D-box. The query is actually asking whether each point is in any of them.
This is not difficult as it seems to be. First, there are actually 8 kinds of different boxes, regarding the ≥ or ≤ sign. We can deal with them by mirroring the coordinate and do the same process 8 times, so we only need to focus on {(x, y, z)|x ≤ xi, y ≤ yi, z ≤ zi} situations. This is done by a scanning line trick. We sort both the queries and the boxes by descending x coordinate. Then each time we need to update something like {(y, z)|y ≤ yi, z ≤ zi} when we meet a box, which is simply done by a segment tree in the range of [1, ymax], maintaining the maximum value of zi on yi so that there is a box covering {(y, z)|y = yi, z ≤ zi}.
My code: 40807344
My 3D segment tree (aka octree) with some constant optimizations passed E.
http://codeforces.me/contest/1010/submission/40822866
The asymptomatic complexity is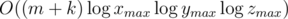 , I believe. This seems terrible but it works.
, I believe. This seems terrible but it works.
Complexity of your solution is definitely not as you described. Even for 10000 queries on the test of type:
your solution works in more than 2s on CF. So for 100000 queries it works almost 30s. https://ideone.com/VnJcp3
I looked through your code and complexity of your solution looks like O(m + log(x·y·z)) per query. These lines of code:
can check all m points through recursive call. I checked it for this test and your in_box(ql,qh,p) above was called 100000 times for 1 query. So your solution has complexity O(m·k).
I'm guessing you have some implementation issue in your octree, but that a nice idea! I tried implementing it in Java, and it's the only 3d range query solution that passed the time limit (577 ms).
Here is some of the other implementation:
577 ms Oct3Tree (https://codeforces.me/contest/1010/submission/40861402)
TLE RangeDTree (https://codeforces.me/contest/1010/submission/40860248)
TLE KDtree (https://codeforces.me/contest/1010/submission/40860860)
I even tried using persistence Kd-Tree, but this didn't quite work either.
I'm interested why the range-tree (which is in the same complexity as the octTree), didn't pass the tests, maybe I'm missing a bug somewhere...
Anyway cool question, I really enjoyed it :)
A round to test who type faster.
could somebody please explain the editorial explanation for div2 E? why we are we considering multiples of gcd only?
Using Euclidean proof? I don't know what it is in English, but only the multiples of gcd make the equation has a solution
For any integer a and b with gcd(a,b)=D, there always exists integers x and y, such that ax + by = D. And here we can use gcd, as D is also bounded by K,in other words (ax + by)mod K = D mod K, so there always exists non-negative x and y.
If we take gcd(a1,a2,...,an,K)=S, we will get the smallest last digit(other than 0) which we can be obtained using the denominations ( K is also included in the gcd because we need the last digit which is bounded by K).
So multiples of S less than K will be the answer because there are the number of denominations are infinite.
Thankyou Hemant.
How are they accomodating for negative coefficients?,like in this eqn a1*x1 + a2*x2 = c , if some xi is negative then?
If you try to do extended euclidean algorithm by hand, you will see this works for negative coefficient.
Simple case:
ax + by = d, where d = gcd(a,b)
In many euclidian algorithm you define gcd(a,b) recursively like: gcd(a,b) = gcd(b, a mod b) and base case gcd(a, 0) = a
Well actually, we know already x and y values for
ax + by = a (here x = 1, y = 0)
and
ax + by = b (here x = 0, y = 1)
Now we can use these values to find (x,y) such that
ax + by = (a mod b)
Lets say (a mod b) = a — kb. K is just a/b in integer division.
Now say we know xa,ya, xb, yb where xval * a + yval * b = val.
We can use algebra to find:
x(a mod b) = x(a — kb) = xa — k*xb (basically taking the first equation — k*second_equation and distributing)
and use same logic to find y(a mod b)
Ok so now you can recursivley apply this logic until you find good coefficients x and y that make it so ax+by = gcd(a,b).
Of course, try some examples and you will notice some of these coefficients are negative. (since a mod b is just a-kb, it's not surprising)
Now you can extend this to more than 2 numbers because gcd(a,b,c) is just gcd(gcd(a,b),c) and so on.
But... Why x_i < 0 does not affect the calculation to problem (Div. 2) — E, can you explain me.
Tutorial: Here some xi<0, But Natasha can add for each par a sufficiently large number, multiple k, that xi became greater than zero, the balance from dividing the amount of tax on k from this will not change.
what does it mean? add sufficiently large number, multiple k, that xi became greater than zero.
I think that considering negative xi means that Natasha receives money from martians (she should only pay to visit Mars). Example 12x1 + 20x2 = gcd (12,20) = 4 where x1 = 2, x2 = -1. How is x2 made positive?
Once you find one set of coefficient, actually you can find infinite amount (and you can adjust the coefficients to be positive one)
for example:
ax + by = c
but also means
a(x+b) + b(y-a) = c
And you can "adjust" it.
Solution Link : http://codeforces.me/contest/1011/submission/40827796 What is the error in the above solution? I used binary search for problem Div2C. The solution gets accepted if my high for binary search is 10^9+1 but not for 10^9.
Comparing double value with integer gives you 1000000000.0000000 > 1000000000. So 1000000000.0000000 is considered wrong(as it exceeds 10^9) which in fact is right. Did the same mistake
It is because, your first binary search.
Let's say that l=10^9 and r=10^9 -> mid=10^9. when you called check(mid) function it returns true. It is obviously if you called check(mid-1), it will also return true and now your r will become 10^9 — 1; That's why when your first binary search is done, it will produce -1 (l>r)
when l=r=10^9 and if check(mid) return true then obviously check(mid-1) will return false.
Using both mid+1 and mid-1 doesn't work in this problem because you are ignoring all the real values from (mid, mid+1) and (mid-1, mid) when you transition in your search. Eventually it means even when you convert it to doubles, you will not find an answer because the integer bounds were wrong.
I didn't get. Int the second search, I am iterating 200 times from mid-1 tomid which covers all the real values.
Yes but you still do some "cutting" in your integer solution, and the incorrect bounds can carry over to your floating-point search because doing +1 and -1. Maybe it would work with 1e9+1 or mid+1, because of the offset, but the integer binary search is unnecessary and fundamentally wrong. It would be better if you started with floating point in the first place and fixed the iterations.
Can someone please let me know why was I getting Runtime Error in test case 8 on Div2 Problem C? Code
Update : Extremely sorry, my link to code went wrong. Here is the Code
Because n is up to 1000, and you collect both b[i]'s and c[i]'s into a, the size of a must be at least 2n.
Can someone share some good practice questions similar to 1011F.
Thank you.
Hey guys, can anybody help me with this BS solution for div2 C ? code
It gives wrong answer on test case 58.. I know it is precision problem since an iterative BS solution works if I do like 50+ iterations. But how should I fix precision when I have this non-iterative code, should I just change EPS value ?
The answer in this test case is 109.
If you write
hi=1e9+EPS, then your solution will be accepted.Oh, I see the problem.. Thanks!!
can someone explain me the Div2 D question, not getting what is being asked in the question.
You want to write a program to "guess" a number chosen by the judge.
You can print out a number y, to which the judge will return you some information about whether the actual number, x, is less than, greater than, or equal to y (your guessed number).
But sometimes the judge will lie and tell you x is less than y when really its the other way around. But the judge lies in a specific pattern of length n.
Your program has to determine this pattern by guessing in some strategy, and after knowing this sequence try to guess the number x.
1011C (FLY) Can someone please explain how we arrived at the equation s+x=tx
total mass=mass that all fuel can transporttotal mass=mass of rocket with fuel that not used in this iteration+mass of fuel that used in this iteration= s + xmass that all fuel can transport=fuel coefficient*mass of fuel that used in this iteration= txs + x = tx
Thanks for explaining :)
For 1010E : Doesn't a 2 dimensional segment tree take m² of memory ? How can this solution work without MLE ?
Editorial says: "let's create a compressed two-dimensional segment tree". It takes only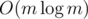 memory.
memory.
If you allocate nodes on demand its only qlogm (q is amount of queries)
Hey guys, In 1011C — fly can someone point out the error in my code. It fails for test case 58 and is accepted when I increase upper bound of BS from 10^9 to 10^9+1. The reasoning is as follows for test case 58. L will keep approaching 10^9(as check(l) is false) until r — l < eps. At which point it enters the block and check(r) must be true. code
The answer in this test case is 109. When you call check(109), it returns false because of presicion error.
Thanks for replying. If that's the case then check(10^9) should return false even if I increase my upper_limit by one. However, when r = 10^9+1, it gets accepted (my answer is 1000000000.0000009537.) More specifically, can you elaborate more on "precision error".
Computer can't save all infinity digits of real number, because it hasn't infinity memory. So it rounds the number. If the program does many operations on real numbers, this error will increase.
why is it important to flush the output in C/C++. I know that printf() is line-buffered, so wouldn't '\n' flush the output anyway?
No. You can submit this code and this solution will get
Idleness limit exceeded:This solution will be correct if you add
flush.I've already got an
Idleness limit exceededwithoutfflush(). I'm just wondering why doesn't it work with simple'\n'.\nis only character. It doesn't flushes output. I don't know whyprintfmust flush output after\n.yes, '\n' does flush the output, but after searching, it turns out this only works when output is directed to the terminal, which is not the case with OJ. link
I use endl with cout (C++ style). I learned this from a Chinese and its very helpful and ez to use than before, when I only knew about flush and when I forgot to write them, I got wa verdicts with lots of annoyance. Hope it will be useful to you. Happy coding!!!
this code have WA on test 1
problem div1. B 40930214
upd:another submission , now its WA
try
cout << i << endl;instead ofcout << i;You forgot to print newline, problem requires that
UPD: Oh, and if you use std::endl instead of '\n' then get rid of your flush, because then you flush twice (unecessary)
Can anyone explain Div2 E problem: Border. I am unable to understand from the tutorial.
nice problem F
Bro @vladProg i am not getting solution to 3 problem (FLY). Below line..
Plzz help me. ThankYou!
Let t = 1 at least for one t. If we will use x tons of fuel, it can lift or land only t·x = x tons of (fuel + rocket). So mass of the rocket is at most 0, that is impossible.
What's wrong in my solution for third question FLY? Please someone tell.. http://codeforces.me/contest/1011/submission/40804467
There is an overflow of type
long longin your solution. Variablespandp_1can be too big (p = a1 * ... * an * b1 * ... * bn ≤ 10001000 = 103000). If you send thePythoncode for example, it will be accepted, becausePythonsupports big numbers.What's wrong with my approach to problem Div1A? I binary-searched over the initial mass of the fuel. It's giving WA on test 58. Here is my solution
Read this comment thread: link.