Author — vintage_Vlad_Makeev
Tutorial is loading...
Author — MikeMirzayanov
Tutorial is loading...
Author — 300iq
Tutorial is loading...
Author — cdkrot
Tutorial is loading...
Author — cdkrot
Tutorial is loading...
Author — cdkrot
Tutorial is loading...
Author — 300iq
Tutorial is loading...










fuck math.
I should have checked what Swistakk commented on this week.
You mean in the last 9 months :p ?
What profit would you get for doing this xD?
I had a simpler solution to the single-tree part D (unfortunately only finished 5 minutes after the contest). Let f(u, v, k) by the number of paths that go from u back to u in exactly k steps, without going through v (a neighbour of u); v can be -1 to remove the restriction. There are thus 3N-2 states per k.
To compute f(u, v, k), consider that any solution must first go from u to some neighbour w != v, then take number of steps (t) in a path from v to v without going through u, then back to u, then another k-t-2 steps from u to u without going through v. So for k >= 2,
where w ranges over neighbours of v.
Naturally the inner sum should be computed by first computing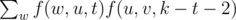 and then subtracting
and then subtracting 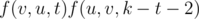 if
if 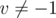 .
.
This is O(nk2), or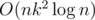 if you use a tree to store the states.
if you use a tree to store the states.
UPD: now i understand
Div2. C For this test case - 14 3 11 10110100011001 Jury's Answer is 20. I think ans is 23. Can someone prove it. Thanks!
let ans=0, step1: 11100100011001 ans+=3, step2: 11110000011001 ans+=3, step3: 11110000000111 ans+=3, step4: 11111111111111 ans+=11,
ans=20
Gotcha. Thanks!
For Div 2 D, I have a few doubts from the editorial :-
what will be the dominating pairs..? I do not understand this..
For {0,4,9,49}, It is mentioned to check all (x,y) <=(50,50), for frequencies of 4 and 9 respectively, but why do we need to check pairs (x,y) with x>8. why can't such pairs be again converted to (X,Y) with detachment of 9..!! ex- These pairs will have same value444444444(9)(49)000.. = 99999(49)00..keeping count of numerals same..
Pair (a, b) is dominated by (c, d) if a <= b and c <= d.
Regarding (2), yes we can check less.
Can someone help me with div2 D? I am stuck on how to figure out such problems, it is not possible to know on pen and paper that n starts increasing by 49 after n=12. I went through the editorial, but could not figure out anything. Can someone help me?
Write a Brute force algorithm and then you can see the pattern
Can you please help me in writing the brute force algorithm?
this works fast for n < 14.
How is 998B solvable by greedy? It is a classic zero one knapsack after the cuts are calculated. Whether to include the cut or not, each cut having a certain cost ("weight") with an overall cost limit ("capacity") ?
The case you are talking about is when we have x odd and even numbers in every segment.
Since all cuts are independent and you want to maximize the number of cuts, it's always optimal to make the cheapest cuts first. Each cut increases the result by 1, so making a higher-weight cut is never better than a lower-weight one.
In DIV-2D/1B why do we solve for {0, 4, 9, 49} ? This part isn't clear to me. And also what does x and y represent?
EDIT: I figured out why we can solve for {0, 4, 9, 49}. I wrote a brute force solution that checks the answer for different arrays. {-1, 3, 8, 48}, {1, 5, 10, 50}, {0, 4, 9, 49}, {2, 6, 11, 51}, {3, 7, 12, 52} all these arrays produce the same number of distinct sums. But why do they all give the same answer?
Because if you add some number x to all n summands, all you do is shift the possible values by x*n.
Can someone explain problem Div 2 D in a better way ?
Maybe I can help you if you formulate an exact question.
I first thought of the problem as to distribute n into 4 (I, V, X, L) such that they get one amount only once (to avoid same number), but as n was large i dropped the idea to go for combinatorics. Then i thought the minimum number that can be generated is n and the maximum is 50*n. Can't we generate all the numbers in between ? I didn't get the intuition behind the editorias approach.
Well, we can't generate them all, but we can generate most of them.
To be precise, we do the following: some numbers have multiple representations, and that is not only about order of digits.
To get rid of it, we introduce some ordering on the representations (by representation I mean (number_of_1, number_of_5, number_of_10, number_of_50).
It turns out, that good ordering is somewhat lexicographic: we want the number_of_50 to be larger, if tie, the number_of_10, and so on.
And then, if we count each number only in it's maximum representation, we win.
So we somewhat need to examine all possible maximum representations, and count how much number have this representation.
Since there are quite a lot of maximum representations, we examine only (number_of_5, number_of_10) part of them -- it turns out that rest can be covered by formula.
Can you share your code with this logic ?
https://pastebin.com/fiZj971x
My submission maybe help you. https://codeforces.me/contest/998/submission/39881689
I am not getting the purpose of loops you are running ? Can you help me understand ?
For the editorial of B div. 1 and D div. 2 when you explained about that other solution in the brackets you said that "you can easy proof a lowerbound like 50 or 100, but it is, in fact, 12", but in fact it is grammatically incorrect. Here easy is an adverb so you should write easily.
Grammar Nazi Spotted !!
I also don't understand D. Please forgive our stupidity and write an editorial understandable for all of us !
It is really difficult to understand. I hope someone explains it in a simple way.
saying more simpler is incorrect. just "simpler" is the right way
Can someone explain the purpose of this factor in the first formula for 997C:
(-1)^(i + j + 1)EDIT: nevermind, it's part of the inclusion-exclusion formula, hadn't heard of it before.
On problem B Div.2, the limits made possible a three-state knapsack-like DP solution (which was what i did). Was that intentional? Because the greedy solution would easily pass for a larger constraint.
Yes, we decided that it is good to allow dp to pass as well.
In div1 D there is naive dp on tree. Lets dpv, j will be number of cycles that starts in vertice v and ends in vertice v and uses only vertices from subtree (we consider tree roodet in this part). Now how to count for v if you know all dps for children lets sum all the dps of chilren in one vector called for example a in details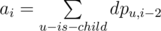 minus 2 because we need to go to u by edge and go from u to v. To receive dpv vector from a we need make following k times: nexti = aj * ai - j than a = nx (you know simple convolution without FFT) And dpv, i will be sum of ai on every iteration of convolution. After bottom-up do similar second dfs top-down. And thats all. But this solution have time complexity
minus 2 because we need to go to u by edge and go from u to v. To receive dpv vector from a we need make following k times: nexti = aj * ai - j than a = nx (you know simple convolution without FFT) And dpv, i will be sum of ai on every iteration of convolution. After bottom-up do similar second dfs top-down. And thats all. But this solution have time complexity 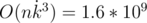 with a lot of MODULO operations it will never pass 7 seconds (I think). And crucial part of solution is to notice that dpv, i = 0 when i is odd(because it is a tree and to make a cycle you need to pass edge even times). Thus complexity is O(nk3 / 8) = 2 * 108 which got AC. See submission for details
with a lot of MODULO operations it will never pass 7 seconds (I think). And crucial part of solution is to notice that dpv, i = 0 when i is odd(because it is a tree and to make a cycle you need to pass edge even times). Thus complexity is O(nk3 / 8) = 2 * 108 which got AC. See submission for details
Do you think that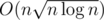 is a good complexity?
is a good complexity?
Can we have Swistakk's seal of approval for complexities? :P
I don't know what you're complaining about. Cutting that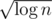 is a factor 4 speedup. It's not as good as the famous bitset optimisation, but it still counts!
is a factor 4 speedup. It's not as good as the famous bitset optimisation, but it still counts!
Cutting n2 from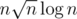 is
is 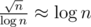 optimisation so it counts too!
optimisation so it counts too!
Div2 E is really beautiful!
I think my approaches of Div1 CDE are all different from the editorial...
Div1 C: You can try to count 'unlucky' grids by ensuring that all rows and columns contain more than one color.
If we only need to ensure all columns contain more than one color, that is fairly easy: (3n - 3)n
Let's try inclusion-exclusion principle on rows, by enumerating the number of rows i with only one color. If these rows themselves are of same color, the ways are: 3Cni(3n - i - 1)n, because every column should not be filled with that one same color. Else the ways are: Cni(3i - 3)(3n - i)n.
So we can get a formula for the answer straightforward: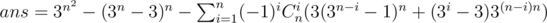
Div1 D: be similar with https://codeforces.me/blog/entry/60357?#comment-441843
Div1 E: (upd: simplified the solution a little bit.)
Notice that a subsegment is good iff max - min - len = - 1, and for any subsegment max - min - len ≥ - 1, so what we need is somewhat minimum.
Let's try to find all good subsegment by enumerating the right end, and use a data structure to maintain the possible left ends. If we just store max - min - len in every left ends, possible subsegments can be found by calculating global minimum and its count. When the right ends move right, max - min - len can be maintained by several range adding (maintain two monotonous stacks, etc.).
For a query [l, r], we need to add up all good subsegments with right end ≤ r, and left end ≥ l. We can maintain a 'count' in every node, and when the right ends move right, we should add 1 to the 'count' of nodes with minimum value. This can be done by simply maintain two tags (one for 'max-min-len' adding, one for 'count' adding) on the segment tree. For details you may refer to 39860384.
If we only need to ensure all columns contain more than one color, that is fairly easy: (3^n - 3)^n Can anyone/@TLE explain?
Edit : got it
A solution for div1D with complexity O(n^2k) also passed :D
Can you explain the last two terms of "ans" for Div1 C in more detail ?
Well I think I've explained thoughly above, they just come from above arguments and the inclusion-exclusion principle. Is there any point unclear?
Let me try to explain the formulae.
I'll assume you didn't get where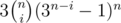 and
and 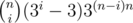 came from.
came from.
As for the first one: you want to colour exactly i rows in a certain colour. How to do it? Just choose i rows, which is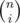 and there are three colours that you can choose, so
and there are three colours that you can choose, so 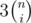 . Now you want to choose colours for the rest of the squares, there are (n - i)n left. Normally you'd count the ways like 3n(n - i) but there can be such painting that there are columns with the same colour, so you have to cross out all such column paintings that have the colour you have fixed on the previous step. To count 'good' column paintings you should apply inclusion-exclusion principle, namely
. Now you want to choose colours for the rest of the squares, there are (n - i)n left. Normally you'd count the ways like 3n(n - i) but there can be such painting that there are columns with the same colour, so you have to cross out all such column paintings that have the colour you have fixed on the previous step. To count 'good' column paintings you should apply inclusion-exclusion principle, namely 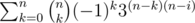 which is equal to (3n - i - 1)n. You should know this formula, or at least be able to prove it. The multiple 3(n - k)(n - i) says that you fix colours of exactly k columns and arbitrary paint (n - k)(n - i) remaining squares.
which is equal to (3n - i - 1)n. You should know this formula, or at least be able to prove it. The multiple 3(n - k)(n - i) says that you fix colours of exactly k columns and arbitrary paint (n - k)(n - i) remaining squares.
The second one. You pick i rows again (which is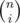 ) and say that each of them can have any of three colours, there are 3i ways to choose three colours for i rows. Don't forget, that we dealt with same-colour rows in the previous step, so we should subtract 3 ways to paint these i rows. Now you know where
) and say that each of them can have any of three colours, there are 3i ways to choose three colours for i rows. Don't forget, that we dealt with same-colour rows in the previous step, so we should subtract 3 ways to paint these i rows. Now you know where 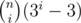 come from. You choose colours for the remaining n(n - i) squares. You know, that there can't be same-colour columns as at least one of chosen i rows have different colour, thus this is a simple case of 3n(n - i) ways to choose colours for them.
come from. You choose colours for the remaining n(n - i) squares. You know, that there can't be same-colour columns as at least one of chosen i rows have different colour, thus this is a simple case of 3n(n - i) ways to choose colours for them.
In the resulting formula, while summing these terms we just need not to forget to multiply ( - 1)i because of inclusion-exclusion principle.
Thanks for the explanation. Btw, (3n - i - 1)n can just be devired from that we can paint the remaining of every column arbitary, under that you should not paint some column with that one same color.
Great Explanation. Thanks
What is "sqrt-blocking"?
sqrt-decomposition, i.e. divide the array into sqrt-sized blocks.
Hi, can you explain what does "history minimum" mean?
Alright. So what we want to do is that when we move right the right end, record the current value to all left ends, for every left end maintain all records' minimum and count. For the sake of simplicity I just called it 'history minimum'.
I've simplified the solution now, hope it helps.
In div1 C, could you please tell me how to calculate all values of pow( pow(3, n — i) — 1, n) for i from 1 to n in O(n) time? I can only understand a O(nlogn) method.
I only know O(nlogn) method too...
Thanks for explanation and I have used your approach in Div1C but I am getting TLE 39894941 my Java code
Java is slow, maybe you just need to do some constant optimizations :P 39949226
thanks!!!!!
Can anyone explain how to compute the mod of large combination numbers? Thanks
see this
can someone please explain me why this solution gives incorrect answer while this one is accepted?
If someone is interested in knowing reason for common difference is 49?
Total distinct pairs : 49There are only 49 distint values of n%49.Lower Bound : 13“Div 2,problem A” Why in 5th test answer 9 1 1 1 1 1 1 1 1 1 Is incorrect?I suppose,it is quite possible.
you have to print the indices of the packets that Grigory get,and he cant get some index multiple times
ohhhhhhh....i did fatal mistake.Thanks for the answer)
Anyone managed to squeeze O(n^2k) in Div 1D?
I really didn't get the editorial explanation of Div2 D. Can you please write the editorial in a more ellaborate way and provide us some pseudocode?
For those people who want code for div2.D using editorial method
cdkrot In div2 D, in the set {0, 4, 9, 49} can we argue that if sum of two sequence is same then one of the two sub sequence is present (44444444 == 999900000) and ((49)00000 == 999994). Are there any other cases left?
Edit: Got my mistake
There should be something wrong with the second picture of Div1.D The picture doesn't contain point (3,2) and (3,1) but there should have them
I had difficulty understanding Div2D/1B so I hope this helps :)
code with explanation
Thank you so much :D Actually helped me out.
Thank you buddy .This was the best explanation
However what is the purpose of val doing in the solution?
oh sorry its not meant to be there, i forgot to delete it after debugging :p
I rate this explanation 49/5
Well explained !
please add source codes for better understanding..
"if we have at least nine digits "4" than we can convert them no some number of "9" digits, and fill the rest with zeroes."
can anyone please explain this line a bit
4+4+4+4+4+4+4+4+4 = 9+9+9+9
Here's my approach for 998D (997B):
Let: nL, nX, nV, nI — no. of L, X, V, I in a particular permutation (resp.). I found 3 ways of converting between the letters: 9X=1L+8V; 9V=4X+5I; 5X+1V=1L+5I;
So that if any permutation which has either (nX>=9) or (nV>=9) or (nX>=5 && nV>=1) then we can show that there are a permutation which satisfies (nX<9) and (nV<9) and (nX<5 or nV<1) that yields the same result. And we will only count those permutation.
In my code, I used brute-force to precompute the answer if n<20 (I know we only need to precompute for up to 12 only if we are using this algorithm, but that doesn't matter). Then, I count the permutation using 2 nested loops for the value of nX (from 0 to 4) and nV (from 1 to 8). The remain (n-nX-nV) spots are used for L's and I's, which there are (n-nX-nV+1) different permutations. One exception is when nV==0, for this, nX can reach to the max. of 8.
The algorithm is O(1). One thing from this task that I'm still questioning that how this algorithm works perfectly without my apparent proving. I wasn't really sure about this at first because I cannot prove that this way of counting permutation doesn't count one value twice, but it worked!
Code (C++14): 39843685
Solution for 998D (Python 3, 108B): Code You can write a small program, try some numbers, and you'll find the rule.
For Div1 C:
Why is i + j + 1 exponent,and not just i + j. And how you know what is exponent in this kind of problems overall? Any advice?
This is my proof for div.1 B/div.2 D.
We need to find (x, y, z) such that x + y + z ≤ n, while counting those (x, y, z) only which result in distinct values of 49 × x + 9 × y + 4 × z. Let's count only tuples (x, y, z) with highest values of x, y, z in the order x then y then z.
Few observations and inferences:-
If z ≥ 9, we can always replace atleast 9 4s with 4 9s, therefore z is restricted to z < 9. Note that for z < 9, we can also never replace z no. of 4s with any number of 49s or with any combination of 49s and 9s.
If y ≥ 49, we can always replace atleast 49 9s with 9 49s, therefore y is restricted to y < 49.
If y ≥ 9, we can always replace atleast 9 9s with 1 49 and 8 4s, therefore y gets further restricted to y < 9.
If simultaneously y ≥ 5 and z ≥ 1, we can always replace atleast 5 9s and 1 1 with 1 49, therefore (y, z) gets further restricted to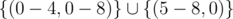 i.e. total 45 + 4 = 49 possibilities.
i.e. total 45 + 4 = 49 possibilities.
Now, since among the above possibilities, y + z < = 12, 49 and only 49 distinct numbers are possible for all arrangements with such x that atleast 12 spaces are left for y and z.
Hence, we can simply brute force our answer for n < = 12 and add 49 × max(n - 12, 0) to our answer.
I got the pattern in 'Roman Digits' problem but still can't understand a bit from the editorial. How they can assume digits to be {0, 4, 9, 49}. Need more detailed and good editorial. How to use the pattern to solve for n = 10^9
It's simple. Think in this way: 1 already occupies all spaces. We then think of replacing some 1s with 50s, 10s and 5s, i.e. at any position, we can only increase the value at that position by 0, 4, 9 or 49.
Div1 D. Can someone explain me why can we make exactly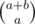 cycles? We want to combine a cycle of length a from the first tree with a cycle of length b from the second one. So, suppose we start from the first cycle, we make some steps along it and then have a choice to proceed in this cycle or make some steps in the second-tree cycle, then, again, some steps in that cycle and a choice to stop/proceed. So, the number of cycles we can get by combination should be equal to the number of different ways of 'stops' we can place of the combined cycle. How is this
cycles? We want to combine a cycle of length a from the first tree with a cycle of length b from the second one. So, suppose we start from the first cycle, we make some steps along it and then have a choice to proceed in this cycle or make some steps in the second-tree cycle, then, again, some steps in that cycle and a choice to stop/proceed. So, the number of cycles we can get by combination should be equal to the number of different ways of 'stops' we can place of the combined cycle. How is this 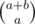 or did I get the idea wrong?
or did I get the idea wrong?
Edit. I get it now. My intuition about cycle combination construction is right, just didn't get how to enumerate them. This is precisely like [stars and bars](https://en.wikipedia.org/wiki/Stars_and_bars_(combinatorics)) with first-tree cycle being bars and second-tree cycle being stars.
good catch, thanks
Can someone help me with que 4 of Div2. How the author arrived at this solution? And how it was decided if pair was good or not?
There is a faster way to solve problem D.We can set 3 arrays,f,g,T.f[i][k] means the num of circles start at i and size is k.The meaning of array T is same as f,but we ignore i's father.g[i][k] means i's father ignore vertice i.Now consider the dp function of f.T & g is similar to f.we can go to any vertice adjoining i.We can't distinguish which point we get in.So construct a general function F(x).now get 1+F(x)+F(x)^2+...=1/(1-F(x)),so NTT can solve it easily.The complex is O(nklogk). My English is poor so I can't discribe it clearly,here is my code
[submission:40032568]I have a question about problem D in Div 2.
What if the maximum representation isn't shortest?
This may happen in general, for example,
Let the set of numbers be {1, 7, 49, 50}
56 = 50 + 1 + 1 + 1 + 1 + 1 + 1, is lexicographical maximum.
56 = 49 + 7, is not maximum, but it is much shorter.
I think longer representation may violate the restriction on number of digits and so that change the answer sometimes, but it seems that this case never happens for the set of numbers {0, 4, 9, 49}. (At least I cannot construct one, nor does it happen in test cases.)
Is there a proof (other than bruteforce checking) that this case never happens for {0, 4, 9, 49}?
(I have known that it is always shortest when any of the numbers in the set is multiple of all other numbers smaller than it, is there a proof for more general case?)
Can anyone please explain how to calculate
(1 + (-3^i))^nin DIV 1C — Sky Full of Stars.This term is available in the final optimized equation in the editorial. But I can't get a way to calculate the above equation in O(N) time. as (-3^i) is a large number which need MOD operation. But If we apply MOD then then original value will changed.
And if we want to calculate the above term using binomial formula then it require O(N) complexity for each i. Then how to calculate this term?
Thanks in advance.
cdkrot please help to understand how to do this or can you provide your solution of peoblem 997C - Sky Full of Stars using the idea described in editorial? Thanks in advace.
Alternate approach for 997B. For a given $$$n$$$ let's find all numbers that can be represented. We can compress this representation by writing it as sequence of intervals. e.g for $$$n=1$$$ the representation is {[1,1], [5,5], [10,10], [50,50]}.
Key observation 1: When $$$n$$$ is large this compressed representation still remains small (about 70). This is because when $$$n$$$ is large most of the representable numbers lie in one large interval.
Key observation 2: Given the representations for $$$\lfloor{n/2\rfloor}$$$ and $$$\lceil{n/2\rceil}$$$ we can construct the representation for $$$n$$$ by combining all pairs.
This gives the following recursive solution with memoisation 81881853.
Is there any clean way to approach Div1 problem B without spotting the observation that we can solve for {0, 4, 9, 49} instead of {1, 5, 10, 50}? If so, would love to see it :)
Alternate $$$O((n + q) \log{n})$$$ solution for Div-1 E using a couple of segment trees and processing queries offline: link
The code is kind of unreadable so I will write a more detailed explanation later, but the key idea is very simple: Just observe how precomputing the leftmost and rightmost position taken by values in range $$$[min(a_i, a_{i + 1}), max(a_i, a_{i + 1})]$$$ for all $$$i$$$ can help us in answering queries. (Focus on the left and right bounds of possibly valid subsegments).