Given an array with N elements you need to choose exactly K non-consecutive elements from it such that the sum of the elements will be minimum.
Constraints:
- 1 ≤ N ≤ 105
- 1 ≤ K ≤ N
- - 109 ≤ ai ≤ 109
I know how to solve this in O(N·K) by using DP(i, m) = minimum sum that can be obtained in prefix i taking exactly m elements.
Can it be done faster than that? Thanks beforehand.
EDIT: I had an idea that was do a binary search on the answer, let's say answer should be less or equal than x, then for a prefix i the values that m can take so that DP(i, m) ≤ x are consecutive so I transformed the DP to DP(i) = range of the valid m values. But the problem with this is how to merge DP(i - 1) with DP(i - 2) in time.











(I) For every 1 ≤ i ≤ n, insert i with cost ai into a priority_queue whose top element has the minimum cost. And keep a linked-list 1, 2, 3, ..., n.
(II) Repeat the following steps k times:
(II.a) Pick the top element x from the priority_queue.
(II.b) Add the cost of x into the answer.
(II.c) Change the cost of x into costprex + costnxtx - costx, where prex and nxtx are the previous and next element of x in the linked-list.
(II.d) Delete prex and nxtx from the linked-list and the priority_queue.
(II.e) Insert x with new cost into the priority_queue.
This works in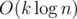 .
.
Thank you. Let me see if I understood you correctly, changing ax into aprex + anxtx - ax every time that ax is on top of the queue what it does is:
and so on right? but everytime you do this you delete prex and nxtx, why is this optimum? Can't it be that later on you can get better solution by taking other x and possibly some prex and nxtx already erased?
It's not clear to me why this is right, could you explain more?
If x is not the minimum after changing cost, you will pick another x.
And the correctness can be proved by minimum cost flow.
I understand the overall approach, but I'm don't know how to handle border cases.
For Example:
If we select a1 (The sequence is 1-based) Then we will push a0 + a2 — a1 into the priority queue. The main idea of the approach is that if we select this element of the priority_queue, it is supposed to "unselect" the original one and select the two adjacent ones such that the k becomes k + 1. However, in the example, if I select the element "a0+a2-a1", the number is selected element remained unchanged because a0 does not exist. however, in the loop k increments by 1.
How am I supposed to fix this problem.
Sorry for Bad English
If you select a1, it means a1 ≤ a2, so you will never choose a2 because a1 is better in both position and cost.
So in such case, you can just ignore the final step.
Tks a lot, your suggestion really helps me implementing the algorithm. At last, I wish you advance to legendary grandmaster soon.
Alternative solution : You can solve it using the so-called "Aliens trick", which is mentioned here. The proof of "convexity" can be done with minimum-cost-flow.