AtCoder Grand Contest 025 will be held on Sunday (time). The writer is yutaka1999. This contest counts for GP30 scores.
Contest duration: TBD (about 2 hours)
The point values will be announced later.
Let's discuss problems after the contest.
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 155 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | djm03178 | 152 |
AtCoder Grand Contest 025 will be held on Sunday (time). The writer is yutaka1999. This contest counts for GP30 scores.
Contest duration: TBD (about 2 hours)
The point values will be announced later.
Let's discuss problems after the contest.
| Name |
|---|



This may not be the right place to post this, but in the AtCoder Regular Contest last week, the editorial for problem E — Range Minimum Queries said that there is an O(n log n) solution as well. I was unable to find it myself. I was just wondering if you could share it here. :)
Let me give it a try.
Sort all the given N number in the decreasing order. Maintain a disjoint set union with N components initially. Start traversing array in the decreasing order and for current element with index i, add edges [i, i+1] if A[i+1] >= A[i] in the dsu similar add edge for [i-1, i] if A[i-1] >= A[i]. After each step maintain the count of possible subarrays with size K which will be summation_of(component_size-K+1). This count will keep on increasing as you are traversing array.
Now any two values can be act as X & Y such that X <= Y if count_of_subarrays_at_Y — count_of_subarrays_atX >= Q. This can be easily calculated by sorting the count and two pointers.
I have not validated this approach.
5 minutes before the contest start!
I give up on D... How to solve it (and if possible, how did you find that solution)?
Hmm... I gave up on B =)
The idea is we can form a bipartite graph with points. Then choose a partition in it.
My idea comes from the proof given in here tutorial to choose greedily the largest partition.
Let's fix the order of points. After that, we can iterate over them and add points greedily.
Checking if we can add a point to the current set is relatively straightforward. Let's find all such integer
aandbsuch thata * a + b * b == d1and do the same thing ford2. After that, we just need to iterate over all these pairs and mark some points as unfeasible when we add a new point to the set.The more interesting question is how to find a "good" order. I did the following: let's sort the points by
(x + y) % modfor several small values ofmod. It's sufficient to pass all tests but one. If sorting by the sum modulo something works pretty well, why not sort them by the difference? Indeed, sorting them by(x - y) % modfor a few small values ofmodis sufficient to pass all the tests. In my case, "several small values" means2, 3, 4, 5, 6, 7for the sum and until we're done for the difference.I solved it by generating a few interesting cases (with many ways to represent
das a sum of squares of two integers) and making random changes to my code until it passes them. I still have no idea why this solution works.You can take a look at my incredibly beautiful code for implementation details: https://pastebin.com/v6YDFrPG.
You can solve it recursively
only remainder by 4 matters for each D, there are lots of cases though
for example, when D1%4=3 and D2%4=3 you can pick all points
when D1%4=0 and D2%4=0 you can solve recursively 4 subproblems with same x%2 and same y%2, using D1=D1/4,D2=D2/4, then merge everything
Other cases are similar, sometimes you take only odd rows, sometimes only odd columns, sometimes with x%2=y%2
My solution is quite simple. Start with the set of all points. If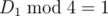 , remove points with
, remove points with 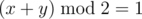 . If
. If 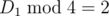 , remove points with
, remove points with 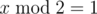 . If
. If 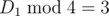 , there is no need to do anything. If
, there is no need to do anything. If 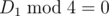 , set D1: = D1 / 4 and check ⌊ x / 2⌋ and ⌊ y / 2⌋ instead of x and y. Do the same for D2. Code.
, set D1: = D1 / 4 and check ⌊ x / 2⌋ and ⌊ y / 2⌋ instead of x and y. Do the same for D2. Code.
Great solution! But it looks like we should delete points with x mod 2 = 1 in case when d mod 4 = 2 and delete poits with (x + y) mod 2 = 1 in case when d mod 4 = 1.
You are right. I fixed it.
If you are finding D difficult, you can try out this question on HackerEarth first. (Problem F of June Easy Challenge 2018).
It's an easier version of D, because there's only one distance rather than 2. :)
Coincidentally, it was asked just two days before the AtCoder Grand Contest.
Can anybody explain solution for B, please?
Also, how can we see other contestant's solution?
You can see everyone's submissions here. Click on Details link in the rightmost column to see the code.
Thanks a lot eatmore. Can you explain B, if you have solved it?
The main idea in B is that for each layer, you can independently decide whether this layer will contribute A to the score and whether this layer will contribute B to the score. Iterate over NA: the number of layers that contribute A to the score. The number NB is uniquely determined from ANA + BNB = K. They contribute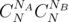 to the answer.
to the answer.
Thank you so much. Now that I look at the problem this way, it looks way more easy.
Earlier, I was trying to find out the number of ways if we paint with only R&B, R&G etc which is ofc way more complex. Thanks again :)
this is simply amazing. I spent 3 hours on this and this simple solution never struck my mind.
Is this the way to solve B? Unfortunately I got TLE on a variant of it from test cases 22 onwards.
Let (br, bb) be the a pair of reds and blues that appear in the tower (we iterate over br, between 0 and n to find such pairs).
Then compute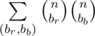 , where those binomial coefficients are taken
, where those binomial coefficients are taken 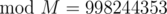 .
.
How to evaluate that sum efficiently? Are the ideas in this StackExchange post sufficient, i.e fast exponentation with Fermat's little theorem? Do we need to precompute all such possible values of the binomial coefficients?
Painting a level green is like painting that level blue and then red. So you can iterate over the number of levels you're going to paint blue (let's call this I). The number of levels you'll have to paint red will be uniquely determined (let's call this j). Then you add choose(n,i) * choose(n,j) to answer.
That's exactly what I describe above.
My problem is in efficiently calculating choose(n,i) * choose(n,j). How?
You can calculate nCr in O(1) using preprocessed factorials and their inverses.
If you fix the number of red, then you just calculate the number of blue one. So all other just calculate binomial coefficents in O(1). It can be done by storing factorial and reverse factorials.
I want to add link to my submission, but I can't find the link to submission on atcoder site.
P.S. I found the link Code
It can be done by storing factorial and reverse factorials.
Thank you.
Aargh why didn't I think of that!
First I took a look at Problem D and thought greedy algorithm with some random_shuffles will work.Then I wrote it and took a long time debugging it. At about 80 minutes after the beginning,I submitted the solution only to see it could pass all but 4 testcases. And I worked on my solution,changed the greedy strategy....But all this don't work and the contest ended! And this is how I got rank 1600+ and got back to blue.So sad.....
I spent a lot of time on that and passed all but two tests :(
I got TL on a single test, optimised my solution for a lot of time and in the end I found out that on test 300 5000 10000 I can only get about 50000 points. :(
Had you found this test by yourself? Or is there a way to see tests in atcoder (after the contest of course)?
I found it myself. You can find testcases of past contests here, but AGC025 is not there yet.
You should prioritize submissions from a contest over those sent later. There is a big queue right now and I've resubmitted my solution to see the result faster. That's stupid.
Limits in F are quite tight. Did you want to fail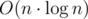 solutions? IMO it would be better to make it like 300 000 and maybe decrease the points for this problem. It wasn't worth more than D+E I think, even if you require the linear complexity.
solutions? IMO it would be better to make it like 300 000 and maybe decrease the points for this problem. It wasn't worth more than D+E I think, even if you require the linear complexity.
Sorry, we completely agree with your idea in general. The main part here is to get anything better than O(n2), and we want to allow them if possible.
However, this time we are quite afraid of O(n2 / 64) with very small constant factor.
Was it easy for you? For me it looks like an impossible problem even with the log factor, while E is quite solvable.
The queue of F was unexpected, we need to look into it.
I wouldn't say it is easy, but my solution is not hard either (English editorial is not available yet, so I can't compare it to your idea). Basically, I'm just simulating the process. Bits which are present in both X and Y are moving to the left on every iteration. Sometimes they "catch up" with bits which are present in either X or Y. Whenever this happens, the total number of 1-bits in X and Y decreases, so there are O(N + M) events, which can be kept track of using a handful of sets. Unfortunately, the constant factor is quite large, and I didn't manage to fit it into TL during the contest.
This solution can be easily turned into O(n) one by storing the bits in a linked list (just one list for both numbers, where element value is a pair of bits, and elements where both bits are zero are not stored), and storing the events in an array of lists indexed by time. Each event holds a pointer to a linked list element. Processing one event takes time O(1+number of elements destroyed), so the total is O(n + k).
I have the same solution. It's the first thing that comes to mind and it turns out to be doable, so the problem isn't very hard.
I have ~1s on a random test but got TLE on multiple tests after submitting (well, maybe I have a bug and it's O(n2) in some case, idk). It would be better to have TL 4-5s. We wouldn't have to care about the constant factor, and the naive bit solution wouldn't pass for sure.
And I simulated one step of the process first in order to make some extra assumptions about the strings (only then intervals of 1's in both numbers are completely disconnected and will never affect one another).
My solution passed without any problems.
solution passed without any problems.
Mine passed in 1999 ms after 7 TLEs.
Getting AC in 1/10 of TL would be some argument in this discussion. You have more than TL/2. A bit bigger constant and you would fight with TLE too.
me in every AGC round : Find E or F pretty interesting, solve it for 1 hours or more, fail to solve, and just give up the round :/
Yea, problems were nice :3 But I think that F>D+E is bad idea, same with E=D+C. Even if problem's difficulty changes strongly in my opinion it shouldn't be worth so much.
Is the following solution to C correct? I thought I had a proof during the contest, but after seeing O(NlogN) in the editorial, I'm not so sure anymore:
We add [0, 0] in the set of segments. Then, for each segment between two integer points, we add to the result the amount of times we need to cross it, i.e. the minimum of the number of intervals strictly to the left and strictly to the right of it. At the end, we output result times two.
My solution for C. Suppose coordinates are only positive. So we want to maximize the maximum length of walk. Person should go first miximum possible right, then maximum possible left. So sort all right ends of segment and all left.
But also we have neggative coordinates, it means that maybe more optimal first go left. But this is the same as going right on reverse coordinate. So run solution, reverse coordinates, run second time. And take maximal answer.
Code
Do rating formulas work correctly?
I showed perfomance higher than my current rating, but got negative rating change.
You can check the formula here.
After checking it, you'll find this (negative rating change) reasonable.
In short, your rating is a weighted average of your performances (over all rated contests). And it weights more for recent contests or high performance contests.
So when you get a new rated contest, it decreases the weight of all other contests. And (in your case), ARC098 and ARC097 have significantly higher performance, which leads to your rating decreasing.
From D editorial, if one construct the graph in the same manner as the proof for bipartiteness, wouldn't the complexity be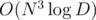 and can be optimized to
and can be optimized to 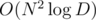 by noticing that the number of edges is not large. How can one construct the graph in O(N3)?
by noticing that the number of edges is not large. How can one construct the graph in O(N3)?
Consider a point. In every row there can be at most four points on that row adjacent to the considered one (two on distance d1 and two on distance d2), therefore total number of adjacent points cannot exceed 8·n. And we can find them all in linear time using two pointers.
Explain to me please what is "invfactorial" in these solutions of problem B O(NlogN) O(N)
It is modular multiplicative inverse of n! with respect to modulus 998244353.
Thank you!
I managed to AC E with simplex with 10000 equations and 6000 variables. Maybe it's overkill but at least for me it was straightforward to formulate an LP. I initially thought E was a creative min-cut/max-flow problem which was why I went for the simplex solution.
When the test cases will be uploaded?
how to do B. I cannot understand reverse factorial method. where can i read upon that. I have read a couple of submissions but cannot understand this inv[] array which is the reverse fact. why to do that?
Because number of ways to choose k items out of n is n! / (k! (n — k)!)
I tried to submit using simple factorial formula but that definitely fails. I think this inverse is to get 1/k! and 1/(n-k)! in modulo constant. I got through the wiki page and i think i understand some stuff. still struggling though.
Have a look at this tutorial : Link
Do anyone have their proof for solution of problem C, I tried hard to prove my algo but I couldn't, thanks in advance.
When will the tutorial for C appear?
I have solved problem E with O(m * log(n) * log(n) + n * log(n)).
The idea is we construct new graph G' where each node is a path.
We divide path u -> v to u -> lca(u, v) and v -> lca(u, v) and we add an edge between these paths in G'.
Now we store paths by set, in each node u, we will know s[u] is set of paths go through the edge from u to par[u].
Now if s[u].size() == 1, we add 1 to answer.
If s[u].size() > 1, we add 2 to answer and we will choose 2 paths from set.
Suppose id of the paths we choose are x and y, we add an edge (x, y) in graph G' and we paint all common edges of path x and path y color 1 (initially all edges have color 0).
Note that we only do the above process when edge u -> par[u] have color 0.
I somehow prove that graph G' is bipartite graph but i'm not sure about that because the limitation is 2000 :D.
Please correct me if i'm wrong or can anybody give me a strong proof ?
Link to my code: https://agc025.contest.atcoder.jp/submissions/2625766.
When will the tutorial for F be translated?