The following submission 52361614 contains a user-defind C++ class modulo for (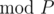
) modular arithmetic, where P is a prime number and all numbers are normalized to the interval [0, P - 1]. The modular division operation y / x is performed by means of multiplying the modulo number y times the modular multiplicative inverse of x computed using the modular power operator xp. The class includes another class modulo::factorial for computing modular factorials n! and modular binomial coefficients m-out-of-n.
The C++ class can be used by Codeforces as any other shared library in the public domain.
Thank you.
I appreciate the class, but many things seem superfluous. For example, the %= operator seems of little use, since in general taking a number mod a followed by mod b doesn't have very nice properties. Same goes for the relational operators, since generally an ordering doesn't make much sense modulo p (eg. we do not have a < b implies a+c < b+c).
I appreciate your feedback. The %= operator and most of the relational operators were deleted from the modulo class. Using friend operators for '*', '/', '+' and '-' is basically syntactic sugar that attempts to make using a modulo object in an expression very much like using an integer variable. Note that all the (mod P) normalization operations are performed implicitly by the class function after performing the intended integer arithmetic operations. So, there is no need to explicitly write this normalization call, and there is no mistake as well in omitting such normalization step after an intermediate modular arithmetic operation.
in the power function, why do you return 1 if value == 0?
Thanks for the comment. Yes, this is an incorrect return value. The correct return value should be 0 when p is strictly positive.