Всем привет! Завтра, 8 апреля в 15:00 MSK пройдет третий отборочный раунд Яндекс.Алгоритм 2018. Перейти в контест можно с сайта Алгоритма.
Раунд подготовлен мной с большой помощью от GlebsHP, а также всех, кто поучаствовал в прорешивании. В задачах вам предстоит помочь некоторым из моих коллег по Яндексу справиться с разными жизненными (и не очень) ситуациями. Всем удачи!
Вход в контест
UPD: Раунд завершился! Наши поздравления Merkurev, jcvb и Um_nik, показавшим наилучший результат в раунде.
Отборочный этап завершился и теперь известны имена участников, проходящих в финал соревнования в Санкт-Петербурге: таблица результатов.
Также доступен разбор раунда (ENG only).
Всем спасибо за участие и до новых встреч!
Важная информация для участвующих в Открытом Кубке
Here are the past Yandex Algorithm Round 3s:
2013
2014
2015
2016
2017
Good luck to everyone participating!
I don’t know why it’s downvoted, but this is really helpful, thanks!
По правилам, если один участник заработает футболку за два разных трека, то ему дают одну. А куда уйдёт другая?
There is no link yet at https://contest.yandex.com/algorithm2018/ to the contest itself
Yandex contest links are like CF point distribution. It will appear in the top panel next to the optimisation and ML round "soon" (or "shortly before the contest").
And occasionally it is shown in the blogpost after the contest starts.
It should be available at the algorithm page now, but for your convenience I also added it to the body of the post. Good luck!
https://contest.yandex.com/algorithm2018/contest/7989/enter/
The link shows me Round 2 of ML track, not Round 3. Note that I'm not 100% sure that I use the correct Yandex account, since it's been a while.
It should be available at the algorithm page now, but for your convenience I also added it to the body of the post. Good luck!
How to solve E
The following passed in upsolving (after the end of the contest :( ). The main observation: we can solve the problem from highest to lowest bits greedily. I.e., first find how many numbers among x and y contain bit 219, let it be X19, Y19. Say A19 = min(X19, Y19). Now, let's define X18 as "max number of x's with bit 218 we can choose, assuming we also choose A19 numbers with bit 219 in addition". And so on; the answer is
.
How to compute Xi, Yi? Naive approach would be max-flow, just build a graph with numbers on one side and bits on the other. It is even incremental (we go over bits and add new edges to the sink). Unfortunately, this gets TLE even with optimizations (at least, in Java).
Now, an improvement: we can compress the graph significantly for most of the iterations: when computing Xi, we're interested only in the last 20 - i bits, so if 20 - i is small, we replace n with 220 - i in graph construction. This already fits in TL, even in Java.
I'd be interested in a faster solution, though.
We can apply Hall's Theorem to check if a certain Ai is valid.
By the way, how to prove that we should choose Ai greedily?
Suppose you have a solution that isn't as greedy as possible i.e. A_i is suboptimal. Then there is some edge you can add with weight 2^i. To add it, you may have to discard one or two other edges from your match (those sharing a vertex with your new edge), but they have weight at most 2^(i-1), so you haven't reduced the total weight.
Suppose that x1, x2, y1, y2 = 2, 1, 3, 2.
In the optimal solution, we should make pairs (x1, y2) and (x2, y1), and in this case A1 = 1, A0 = 1.
Consider a suboptimal solution: pairs are (x1, y1) and (x2, y2), and A1 = 1, A0 = 0. But we need to discard an edge of weight 2 to improve this.
You're right, my argument doesn't work.
Here's a new one, although a lot less intuitive: consider the solution based on Hall's Theorem. If you decrease Ai by 1, what is the effect on the rest of the solution? Ai + 1 will increase by at most 1, Ai + 2 can increase by at most 1 etc; and the increases sum to less than what you've lost.
I think it needs a bit more work to make it formally correct, but that's the outline.
That's exactly what I did, and it passes in upsolving (you also need to use a Mobius transform to make it O(2^N*N) rather than O(3^N)). Unfortunately I only realised this solution 90 seconds before the end of the contest and didn't have time to code it.
I used Hall theorem in the second part of my solution in order to compute maximal possible Xi and Yi. So we only need to know number of vertexes, which have at least one common bit with some mask, and we can compute it offline in O(2^20 * 20), as I did.
I use flow graph and get AC in upsolving.
This is my AC code
First of all, we want to maximize number of 219 edges, then number of 218 edges and so on. To do this we will use Hall's marriage theorem. Suppose we have already fixed the number of edges 2p for all p > k and now want to find the number of edges 2k. According to Hall's marriage theorem we should satisfy some inequalities of the form: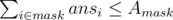
, where Amask is the number of such x in one of the input arrays that x&mask ≠ 0. Since ansi = 0 for i < k (for now) we can check these inequalities only for mask which has lowest 1-bit on position k. To calculate Amask we can use or-convolution. From these inequalities we can deduce the biggest possible ansk.
Complexity —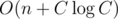
You may also check the official editorial, you may find the link in the post.
What is corner case in C??
Also what is the cut off rank to be in top 256 across all elimination rounds
my problem in C was integer overflow
My problem was using
(x+y)%2to categorize bishops into two arrays.what was wrong with that????
it may be -1 0 or 1
-1 % 2 = -1Regarding 2 : Refer this link. Until Round 2, the criteria was to get a best rank of less than 163, It will get modified to a tighter rank after round 3.
Cut off can be seen here: https://contest.yandex.com/algorithm2018/algo-results/?p=6
How to solve D? Was it Binary Search?
Yes, we just make binary search and then for every vertex compute Li, Ri — the left and the right border of possible value, according the Lj, Rj in the descentants, receiving with DFS. Checker — if some Li > Ri, answer is false.
How much time it is working on C++?
1,6 second with 200 iterations of binary search
Now that the top 256 in Algorithm track is decided, When will you send t-shirts? :D
It seems like the test data for F is weak. I just submitted a solution that completely ignores that the bottom row and top row are adjacent, and it passed.
Is It Rated?
When will test data for E in gym be fixed?
It fixed now and all the solutions is rejudged.
Problem D, as I think, can be solved by extraction connected regions consist of '*' with numbers on borders. This regions are trees and for every such tree target value is max(|num1-num2| / distance(num1,num2)) for every pair numbers. But I does not know how to solve this task fast. Can anyone help?
Is it possible to look at other people's submission, e.g. in CF Gym ?
There is some part in editorial that I don't understand. Would be very helpful if I could take a look at accepted code.
Thanks in advance.