XVIII Open Cup Grand Prix of Gomel takes place on Sunday, February 18, 2018, at 11:00 AM Petrozavodsk time.
The link to the contest. You need an Open Cup login to participate.
I'm the writer of all the problems. Let's discuss them here after the contest!










Do you believe in extraterrestrials? what if they appear and ask you to find ramsey 5,5 number? what will you answer?
After some csacademy rounds, I thought that the best are minimalistic statements, but even tourist can write cute problem stories :)
How to solve B?
First note you need to maximize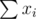 subject to
subject to 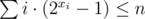 (here xi is the number of ones in f(a, i)). Now increasing a xi by one 'costs' i·2xi. Binary search over the maximum cost that you use.
(here xi is the number of ones in f(a, i)). Now increasing a xi by one 'costs' i·2xi. Binary search over the maximum cost that you use.
Is there greedy first binary search for i = 1 find max x1 then max x2 for n — 2xi + 1 and so on...?
No, you binary search over the maximum cost for which you use 'all options'. To check if m is possible, check if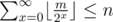 (here
(here 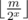 counts the number of i for which i·2x ≤ m). After the binary search you can use whatever you have left for options which cost exactly one more.
counts the number of i for which i·2x ≤ m). After the binary search you can use whatever you have left for options which cost exactly one more.
Could you share the feeling when you see no Chinese team solved the problem J?
Lol, you guys should write some problems about Mahjong hands evaluation :)
(Note to readers: this contest first appeared at Chinese Winter Camp two weeks ago. 25 teams, 0 submissions for problem J.)
Well, I anticipated that it could go either way :) Such a scenario was more likely with Chinese teams -- Russian-speaking participants are more familiar with this game, even though this particular modification is made up by myself and obviously not played by anyone.
If you ask about feelings -- I was slightly worried that the problem statement was difficult to understand. In Petrozavodsk & Open Cup the first correct attempt came in during the first hour, and then a dozen of non-Russian-speaking teams solved it as well, so hopefully it was good enough.
We spent 40 minutes to understand rule of "Fool's Game".. Do Russian competitors know it already?
Yes, but it's modified. If second has 2 jokers, he loses, otherwise he wins by taking all cards that first tosses until first only has jokers.
Is there any simple proof? We solved J without any proof :(
As I said, if second has at most 1 joker, his optimal strategy is to never cover and always take cards that first tosses at him. This way first always tosses. In the end the first will take all cards from the deck, so he surely will have at least one joker, which he can't toss, so he will lose. If second has both jokers, then if he always takes cards, then first's hand will get empty in the end, and if he covers at least once, first can use similar strategy and only take cards for the rest of the game.
In Russia it's a well known card game called "Дурак" ("durak").
If I were to choose a card game that every single native speaker of Russian knows the rules of, Durak would be my bet.
How to solve G and K?
K: Factorize N first. Then, inclusion-exclusion works in O(3k), where k is the number of distinct prime divisors of N. It's first enough.
The main challenge is the factorization. Check all divisors up to N1 / 3. Then there are three cases:
Could you explain about inclusion-exclusion more detailed?
Suppose that N = paqb. We want to choose a subset of divisors of N. But there are four things we want to avoid:
Now we get an O(4k) inclusion-exclusion.
To make it O(3k), notice that "choose (1) and not choose (2)" and "choose (2) and not choose (1)" are equivalent (and the same holds for (3) and (4)).
Why N is pa * qb but not p1a1 * ... * pnan?
I assumed that k = 2 just for simplicity, it works for general k.
Here is more or less strict detailed formulation. Assume n = p1a1... pmam.
All numbers in considered set must be divisors of n. Let's calculate number of subsets g(n) we can take having only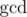 equals 1. That means that for each number pi we should take at least one number having pi with only power of 0 in its factorization. let's denote set of all sets that contain at least one such number for pi by Ni. Then we have to calculate intersection of such sets:
equals 1. That means that for each number pi we should take at least one number having pi with only power of 0 in its factorization. let's denote set of all sets that contain at least one such number for pi by Ni. Then we have to calculate intersection of such sets:
Here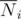 denotes set of all sets that do not contain any number having pi with power 0 in factorization. For single number i holds
denotes set of all sets that do not contain any number having pi with power 0 in factorization. For single number i holds 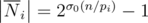 where
where 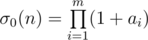 is simply number of divisors of n.
is simply number of divisors of n.
Indeed, we shoud choose some divisors of n such that they all are divided by pi, thus we can first divide n by pi, choose arbitrary subset of divisors and multiply them backwards by pi. After that we subtract 1 to vanish empty set. And for intersection of such sets we have:
Thus answer can be reformulated as Dirichlet convolution using Möbius function:
Now if we would like additionally calculate number of subsets f(n) having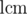 equals n we can write it with quite similar formula:
equals n we can write it with quite similar formula:
Since Dirichlet convolution is associative, we can just calculate
Where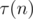 is Dirichlet convolution of Möbius function with itself. It can be found out that
is Dirichlet convolution of Möbius function with itself. It can be found out that 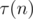 is multiplicative function defined in the following way:
is multiplicative function defined in the following way:
This allows you to solve the problem in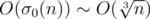 .
.
such hard maths. from where you learn.
Wikipedia
How to solve D and I?
Gaussian binomial coefficient and line graph recognition.
Line graph recognition lol
Now I'm curious how MSU team solved it. Did they derived it from scratch?
It's not so hard to come up with some process building the answer. Something like "take an edge uv, assign xy and xz to its endpoints, realize which neighbors can have x, y, z and yz labels..". I can share my code which received OK after about one and a half hour of debugging with stress after the contest in Petrozavodsk. Also I can explain the ideas behind my solution if you are still interested, but maybe guys from Red Panda had simpler approach.
Yes, basically I expected the contestants to come up with a similar process. From a fairly large number of submissions, it seems that many teams actually did that.
Unfortunately, the devil is in the details, and most teams failed on test cases 4 and 5, which are line graphs of graphs with a lot of small connected components. The only team besides MSU Red Panda who managed to get past them was team Ural FU 1 -- they ended up with WA 35.
One way to deal with ambiguities, which actually only happen in the beginning of the process, is doing a brute force search until the current connected component is large enough. Definitely it's also possible to analyze these ambiguities on paper.
Let q = 1 - p and r = p / q. It's easy to see that f(k) corresponds to the coefficient of Xk of the polynomial PN(X) = (1 + X)(1 + rX)(1 + r2X)...(1 + rN - 1X). So we want to evaluate this polynomial.
Use the following (and FFT):
In fact, no FFT or polynomials are needed as there is a simple formula for f(k).
If we call G(N) = (1)(1 + r)(1 + r + r2)...(1 + r + ... + rN - 1), then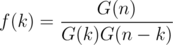 .
.
Why the formula of f(k) looks like this or the one from rng_58's post?
For my formula: simple calculation shows that the probability that the set of people with indices {a1, ..., ak} beats everyone else is ra1 * ... * rak * Ck, where Ck is a constant that depends only on n, k, p. Thus, we are interested in the value of
If we get sk for each k, we can get f(k) = Cksk.
sk is the coefficient of Xk in the polynomial above.
UPD: Now, search "There are analogs of the binomial formula" here.
How to solve H and J?
For problem H:
Assume a < b. If n is even while a, b are odd, then there is no way to complete the journey as you can never travel between two even numbers consecutively by walking or jumping.
Otherwise: if a is even, a valid path with three jumps is
Similarly, when n is odd, the following is valid
and when b is even, the following is valid.
We will also need to check if there are shorter paths, and deal with special cases like b = a+1, b = n, a = 1, etc. The number of possibilities to check will still be O(1).
I've already posted solution sketches in a separate comment, but I'd just like to make a special note here (for those who don't get to read it) that a solution without case analysis, at least in the implementation part, is possible.
How to solve G?
Great chance to know about tourist's musical taste
I'm kind of curious about case 64 in problem K. Was it designed to break integer factorization in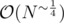 ? (My squfof breaks on it and I could't break it with various random tests.) Did anyone try pollard-rho?
? (My squfof breaks on it and I could't break it with various random tests.) Did anyone try pollard-rho?
Test case 64 in problem K is 999949000866995087 = 9999833. Yes, I've seen a bunch of accepted solutions using Pollard's rho.
Can you give me please the 33th test? I don't know why but I get TLE on it (in Go) while all others pass in less than 30 ms.
This is the first test case with a lot of distinct prime divisors: 914836017997511610.
Please find a brief summary of solution ideas here. Feel free to ask if you have any questions.
Could you explain in problem G how to find intersection of semiplanes in O(n) and tricky moment with "all semiplanes intersect any line x=d at some integer y" more detailed?
In general, half-plane intersection is similar to building convex hull. One possible way to go is to separate half-planes into "upper" (covering point (0; + ∞)) and "lower" (covering point (0; - ∞)), sending "vertical" half-planes into either category (there are none in this problem, though). Then, in each category, sort half-planes by polar angle and perform a scan with stack removing unnecessary half-planes -- this is similar to Graham scan. Finally, we have two polylines and by finding their intersection points we obtain the resulting polygon. Of course, in general case this "polygon" might have infinite area, so additional care must be taken (luckily, it never happens in this problem).
This algorithm works in due to sorting, but the scan part works in O(n). In this problem, since the half-planes are sorted naturally -- their normals look like (i - 1;1) for i from 1 to n -- there is no need in sorting, so the whole algorithm works in O(n).
due to sorting, but the scan part works in O(n). In this problem, since the half-planes are sorted naturally -- their normals look like (i - 1;1) for i from 1 to n -- there is no need in sorting, so the whole algorithm works in O(n).
For the second question, when I said "all half-planes intersect any line x = d at some integer y", I actually meant "half-plane borders" not just "half-planes". Consider any half-plane border, for example, a1 + d·(i - 1) = ri. This is equivalent to a1 = ri - d·(i - 1). The right part is integer when d is integer, hence the left part is integer too.
How does it help in this problem? We have found a polygon representing the intersection of half-planes and we want to find the number of integer points inside it. Let's move with two pointers from left to right and divide it into O(n) trapezoids with legs formed by two of the given half-planes and bases parallel to Oy (well, Oa1). Consider one such trapezoid. Since we are only interested in integer points inside the trapezoid, let's shrink it a bit in such a way that its bases have integer x = d. And now the coordinates of vertices of this trapezoid are all integers -- exactly since both legs intersect line x = d at some integer y. Now, for example, you can use Pick's theorem to find the number of integer points inside the trapezoid, but actually this number is just the sum of an arithmetic progression, since at every intermediate integer x = d trapezoid's legs have integer intersections as well.
guys where can i see the problem statements??
The statements will appear here after some time (down on left side in russian is written to choose the stage) but you won't be able to submit problems unless you have an account.