Подсказка: Когда гласная остается в строке?
Пройдем по строке и выведем только согласные и те гласные, перед которыми не стоит гласной.
Подсказка 1: Никогда не выгодно возвращаться. Там, где вы прошли, не осталось призов.
Выгодно собирать призы в следующем порядке: некоторый префикс отходит вам, остальные — вашему другу (некоторый суффикс).
Можно найти итоговое время по информации о длине префикса. Формула получается 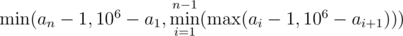 .
.
Подсказка: Для начала решим задачу, обозначенную в условии. Формула — 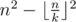 . Каждая подматрица k × k должна включать в себя хотя бы одну строку с нулем. Ровно
. Каждая подматрица k × k должна включать в себя хотя бы одну строку с нулем. Ровно 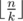 непересекающихся подматриц помещаются в матрицу n × k. То же для столбцов. Тогда нельзя выбрать меньше, чем это значение в квадрате, нулей.
непересекающихся подматриц помещаются в матрицу n × k. То же для столбцов. Тогда нельзя выбрать меньше, чем это значение в квадрате, нулей.
Теперь с известной формулой можно перебрать n и найти нужное значение. Наименьший ненулевой результат при фиксированном n будет достигаться при k = 2. Тогда можно оценить n как 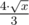 .
.
Теперь найдем k для некоторого фиксированного n. 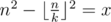

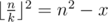

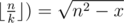

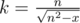 . С учетом округления вниз достаточно проверить только это значение k.
. С учетом округления вниз достаточно проверить только это значение k.
Функция длины пути практически не отличается от традиционной. Можно домножить веса ребер на два и запустить алгоритм Дейкстры следующим образом. Установим disti = ai для всех 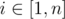 и добавим все эти значение в кучу. Когда алгоритм завершит работу, disti будет равно кратчайшему пути.
и добавим все эти значение в кучу. Когда алгоритм завершит работу, disti будет равно кратчайшему пути.
Подсказка 1: Посчитайте, сколько раз каждое число встречается в сумме всех fa.
Подсказка 2: Попробуйте подобрать точные критерии того, что ai войдет в fa для какой-либо перестановки.
Подсказка 3: Докажите, что ai входит тогда и только тогда, когда все элементы до нее строго меньше (кроме максимума в массиве). Теперь попробуйте решить за O(n2).
Попытайтесь упростить решение и сделать его быстрее.
Легко заметить, что i-й элемент входит в fa тогда и только тогда, когда все элементы до нее строго меньше, поэтому если определим li как количество элементов меньших ai, то ответ будет равен:
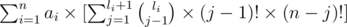
Взглянем на позицию ai, если он на позиции j, то требуется выбрать j - 1 из li меньших элементов, расставить их каким-то образом и расставить остальные. Можем найти все li за O(n log n). Если написать ровно это, то асимптотика будет O(n2).
Попробуем улучшить формулу. Раскроем как:
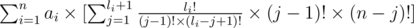
теперь это равно:
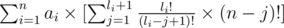
и вынесем li!,
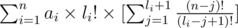
теперь домножим первую сумму на 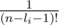 и вторую сумму на (n - li - 1)!, оно становится равно:
и вторую сумму на (n - li - 1)!, оно становится равно:
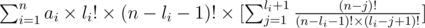
и легко заметить, что это же равно:
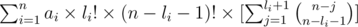
Используем тот факт, что
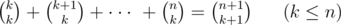
это равно:
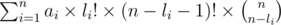
Тогда окончательный ответ равен:
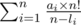
который может быть легко посчитан за O(n log n). Не забудьте, что считать ответ для максимального числа не нужно.
Также есть другое решение, которое можно прочитать тут.
В разборе обозначим n = |s|.
Подсказка: Есть простое решение за время 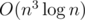 : dp[m][mask] — лучший ответ, если мы рассмотрели первые m символов строки, а маска обозначает, подстроки какой длины мы удаляли. Однако хранить строку в каждом состоянии не позволяют ни ограничения по времени, ни ограничения по памяти. Как можно улучшить это решение?
: dp[m][mask] — лучший ответ, если мы рассмотрели первые m символов строки, а маска обозначает, подстроки какой длины мы удаляли. Однако хранить строку в каждом состоянии не позволяют ни ограничения по времени, ни ограничения по памяти. Как можно улучшить это решение?
Давайте попробуем улучшить это решение при помощи жадных соображений. Так как каждое состояние обозначает возможный префикс строки-результата, то среди двух состояний dp[m1][mask1] и dp[m2][mask2] с одинаковыми длинами ответа, но разными ответами, нам не нужно рассматривать то, в котором ответ лексикографически больше. Поэтому для каждой возможной длины префикса существует только одна лучшая строка, которую стоит рассматривать в качестве префикса результата. А значит, в динамике можно просто хранить bool — можем ли мы достичь такого состояния с лучшим ответом или нет.
Такую динамику необходимо считать особым образом, перебирая длину префикса результирующей строки. При фиксированной длине префикса сначала обработаем все переходы с удалением подстрок (так как они не добавляют нового символа), а затем среди всех позволяющих достичь этой длины состояний dp[m][mask], для которых dp[m][mask] = true, мы выбираем лучший символ, позволяющий перейти к следующей длине префикса (а переход из состояния делается по (m + 1)-му символу строки).
Сложность этого решения  , но оно на самом деле достаточно быстрое.
, но оно на самом деле достаточно быстрое.
Это усложнённая версия задачи G с Educational Round 27. Её разбор можно найти здесь.
Чтобы решить нашу текущую задачу, воспользуемся известным методом динамической связности. Построим дерево отрезков по запросов: каждая вершина ДО будет содержать список всех рёбер, присутствующих в графе на соответствующем отрезке запросов. Если некоторое ребро присутствует с запроса l по запрос r, то его можно добавить по аналогии с прибавлением на отрезке [l, r] в ДО (но вместо прибавления мы вставляем ребро в список, и мы не делаем никаких проталкиваний, которые обычно делаются в ДО с отложенными операциями). Если мы теперь напишем некоторую структуру, которая может добавлять ребро и откатывать изменения, можно решить задачу, обойдя дерево отрезков обходом в глубину: когда мы входим в вершину, добавим все рёбра в списке этой вершины; когда мы в листе, посчитаем ответ для запроса в этом листе (если он там есть); и когда мы покидаем вершину, мы откатываем сделанные в ней изменения.
Какая структура данных нам понадобится? Во-первых, DSU с поддержкой расстояния до лидера (чтобы находить некоторый путь между двумя вершинами). Не стоит использовать сжатие путей, из-за откатов оно не будет ускорять операции в DSU.
Во-вторых, надо как-то поддерживать базис циклов в графе (так как граф всегда связный, то нет смысла поддерживать базис циклов для каждой компоненты отдельно). Удобный способ хранения базиса — использовать массив из 30 элементов, изначально заполненный нулями (обозначим этот массив как a). i-элемент массива будет обозначать некоторое число в базисе, в котором i-й бит является максимальным среди всех взведённых битов. Тогда можно очень просто добавить в базис некоторое число x: переберём все биты от 29-го до 0-го, и если некоторый бит j равен 1 в числе x, и a[j] ≠ 0, то присвоим 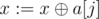 (назовём этот процесс сокращением, он нам ещё потребуется). Если после этого мы получим 0, то число уже является линейной комбинацией базиса; иначе, пусть k — наибольший бит, равный 1 в x, нам нужно просто присвоить a[k]: = x.
(назовём этот процесс сокращением, он нам ещё потребуется). Если после этого мы получим 0, то число уже является линейной комбинацией базиса; иначе, пусть k — наибольший бит, равный 1 в x, нам нужно просто присвоить a[k]: = x.
Такой способ хранения базиса также позволяет очень просто отвечать на запросы 3 типа: сначала возьмём длину пути из DSU (пусть эта длина равна p), а затем просто сократим p, и это и будет ответом.










@BledDest Sir , in problem C , why are we taking only non-intersecting submatrices of size k x k? Here's what my thought process was for the problem C : let's suppose we have a matrix of size n x n and let us consider a submatrix of size k x k. Now to ensure there are minimum number of zeros(i.e max no of 1s), we'll place 0 at rightmost bottom most cell of the k x k matrix and now we'll consider the total number of submatrices of size k x k sharing this 0, and that would be according to me k x k number of submatices. Now if we consider total number of submatrices(intersecting and non intersecting) of size k x k in the matrix of size n x n , then that would (n-k+1) x (n-k+1) , so according to my deductions , the formula should be (n^2 — ((n-k+1)^2)/(k^2)) which is wrong as per the editorial? Could you help me with what am I thinking wrong? Sorry to bother you , if my question is stupid..
The main problem is that you can't always put zeroes in such a way that k × k submatrices are covered by this zero.
For example, let n = 4, k = 2:
According to your algorithm we put the first zero in cell (2, 2) and cover 4 submatrices:
And now it's impossible to put a second zero to cover 4 submatrices we didn't cover previously.
i was doing a silly thing!!, ignore.
This obviously doesn't give us maximum possible number of ones, since for n = 5 and m = 3 we can use the following:
And for n = 5 and m = 2 — the following:
oh yes! thank you for resolving my doubt
@BledDest
if we do:
1111
1010
1111
1010
we have covered all submatrices. now say t=15 , we get perfect square x(>=15) x=16 ,so given 1s =15 hence 0s are 1(16-1) now answer could be 4 3
1111
1111
1101
1111
if t=12 then zeroes can be:16-12=4 so answer is 4 2
1111
1010
1111
1010
and for all t from 16 to 21 answer:-1 isn't that approach right?
Yes, from every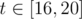 answer is - 1 since if we set n = 4, then we can't obtain anything greater than x = 15; and if we set n ≥ 5, then x ≥ 21 (if we don't consider m = 1).
answer is - 1 since if we set n = 4, then we can't obtain anything greater than x = 15; and if we set n ≥ 5, then x ≥ 21 (if we don't consider m = 1).
but I did it that way,and get WA
I don't know why my D passed. I just ran DFS multiple times (10 times DFS passed) and in each time I took the minimum of that node and all it's neighbors. Is this logic correct or just my luck that it passed. Thanks.
Why do you only use 25 for used?
It passed with 10 only. I still don't know how it works. I thought 2 DFS might be sufficient but it wasn't the case. If I increase the number of times I do DFS it will time out.
I wrote n^2 solution for E, but it got WA#16 instead of expected TLE
Can somebody help me?
cnt2[i]+=(fact[i-1]*fact[n-j-1])%MD/fact[i-1-j];You can't do this. If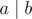 , it doesn't mean that
, it doesn't mean that 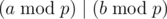 . In fact, you should use the modulo inverse instead of division. (i.e. use a × b - 1 instead of
. In fact, you should use the modulo inverse instead of division. (i.e. use a × b - 1 instead of  .) You can use Fermat's little theorm (i.e.
.) You can use Fermat's little theorm (i.e. 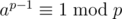 when p is a prime and (a, p) = 1) and quick pow to work out
when p is a prime and (a, p) = 1) and quick pow to work out 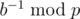 when p is a prime. Otherwise, you can use extended euclidean algorithm instead. Hope this will help.
when p is a prime. Otherwise, you can use extended euclidean algorithm instead. Hope this will help.
Hi, thank you so much for your answer. I did what you said but now i have WA#5. Any suggestions?
Edit: Fixed Thank you again :)
Final solution
I was trying to solve D using a DFS and updating a DP array for each node. Can someone point out what is wrong with my logic?
http://codeforces.me/contest/938/submission/35438377
You should read about the Dijkstra algorithm. I'll try explain the difference with your solution briefly. Doing right way we should take a node with the smallest distance to it and then update the information for its neighbours. After that we should delete this node from our list ( Dijkstra proved it ) and then repeat the first step until we considered all the nodes of the graph. This update in your solution can be wrong very often:
Value in dp[v] is not correct. Example:
Your solution is good without "visited", but then it will be O(n^3).
I guess I'm late to the party, but when I implement this Dijkstra without keeping a count of visited cities I get Time-out, but the solution gets Accepted as soon as I ignore the cities which I have already visited. Also, for some questions like this: 20C Dijkstra, I don't need any visited array to pass the tests.
Could you please explain why does this happen. Obviously, analyzing the Time-complexity is the key, but I find it hard to visualize what's happening. Thanks in advance.
Well, it was a long time ago, so I can't tell a lot. First of all, the main idea of Dijkstra is to keep array of visited cities. Otherwise, you would iterate over cities you've already visited again and again, that's why you get timeout. It's just an infinite loop. What about visualization you can look at wiki page. There is a good gif out there that explains a lot — https://en.wikipedia.org/wiki/Dijkstra%27s_algorithm
Good luck with competitive programming :)
could any one tell me what's the upper bound of n and why it is in problem C? well i mean while iteration.
I've solve it. The range of n should be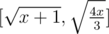 when x ≠ 0 .
when x ≠ 0 .
huangwenlong, can you explain how did you get the upper bound?
Sorry for the late reply. We can get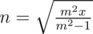 , from
, from 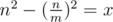 . If x ≠ 0, m should not be less than 2. So when m = 2,
. If x ≠ 0, m should not be less than 2. So when m = 2, 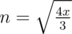 . When m = n,
. When m = n, 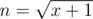 . And we can conclude that
. And we can conclude that 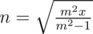 is a decreasing function. So the range is
is a decreasing function. So the range is 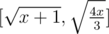 .
.
In E problem,
for every 2 ≤ i ≤ n if aM < ai then we set fa = fa + aM and then set M = i.
Does this statement mean,
or
Please, somebody help.
First code without "else break" is correct.
thank you. :)
Hi everybody.
Here is my code which uses FFT (Fast Fourier Transform) to solve Task E. It doesn't fit in time and memory limits (works well for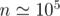 ) but it's good for educational purposes. Actually it has
) but it's good for educational purposes. Actually it has 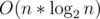 time complexity but FFT has a large constant so it takes around 10secs for
time complexity but FFT has a large constant so it takes around 10secs for 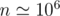 .
.
I don't understand how can we use Dijkstra to actually find closest j for every i. Why does solution in editorial works? Can someone explain?
same question here
consider a new node(v) in addition to all given vertices.This node represents watching a concert. properties: has n edges with weight equal to costs of watching a concert for each vertex. now the problem reduces to single source shortest path between v and all remaining vertices(people from all cities have to (watch a concert so reach node v )in minimum cost) which is solved by dijkstra's.
Thanks bro!!
Consider a vertex having Min(a) (All of them in case of having multiple minimums) and name it "u". The answer for this (those) city is ai. Lest consider the next minimum (Min2(a)) and name it "v". There are two cases. it can go to the city having Min1(a) or just stay there(why?). This property holds for every vertex having Mini(a). It can go to one of those vertexes having Minj(a) with j ≤ i.
Now we assume that it's better for vertex "v" to go to vertex "u". on the shortest path from "v" to "u" there is a vertex (call it "x". Of course it can be "v" itself) which is adjacent to "u". It can be easily proved that best answer for vertex "x" would be to go to "u".
So what it means? every time we find the answer for some vertex we can relax all of its neighbors and then we are done with remaining vertex having minimum found answer.
For problem C: I searched for two divisors of x with same parity and found n & n/k .then re-checked.Can someone explain what is wrong with the code? http://codeforces.me/contest/938/submission/35461430
In C problem
how we concluded that if: floor(n/k)=sqrt(n^2 -x)
then k=n/sqrt(n^2-x) ???
@BledDest Sir, one small doubt, I can't get my head around this problem C,
so suppose x = 14, then can't my answer be n = 4 and m = 4 because if my m = 4 then my whole matrix has zeroes > 0.
Like this:- 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 0
Here i am considering m = 4 that is whole matrix ?
I know many people asked doubts related to problem C but I am still not able to understand this flow ? I know my question is stupid but please help me this last time.
Your answer for x = 14 can't be n = 4 and m = 4, because if n = 4 and m = 4, the maximum number of ones is 15:
BledDest Can you please explain a bit more on time complexity of dynamic connectivity?
As per the approach of editorial , if we have to add an edge to an interval
(L,R)then we will just insert it into segment tree nodes which lie completely under this range(but we will not push it further down).Doubt : Since there can be atmost
log(n)nodes containing that range and if we are doing union by size/rank than it will takelog(n).Time complexity should be :
nlog(n)log(n)log(c)...since each edge can occur in dfs atmost log(n) times and log(n) for their union operation and log(c) for gaussian elimination part first comment in this blog explains it .PS: please correct me if i am interpreting it in wrong way.
You don't have to multiply the logarithm that comes from Gauss and the logarithm that goes from DSU. The union operation is used only in DSU (so it's ), and if it is unsuccessful, then we perform only one operation with Gaussian elimination. So the complexity is
), and if it is unsuccessful, then we perform only one operation with Gaussian elimination. So the complexity is 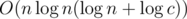 .
.
Sorry my analysis was wrong ,we will first do
log(n)to check for their parents and if they are different then we will union them and if they are same we will dolog(c)(new cycle) for gaussian elimination...so basicallylog(c)+log(n)for each edge during dfs.thank you so much it is clear now.
Could someone explain more about the simple O(n3logn) dp solution of problem F mentioned in the tutorial?
dp[m][mask] has an O(n^2) number of states, and in every state we traverse O(logn) position to decide which we use, and we use string compare to judge which we choose so there is another O(n)
ps:"abcd--> abd --> a" is equal to "abcd --> acd --> a". So we can choose 2^i in turn.
Far better than awoo's editorial. Kudos!
A direct explanation for Problem.F. Let's denote dp[i][j] as the i-th character of the minimum substring after we remove (j-i) characters from S[1...j].
Let i iterate from 1 to the length of result, and let j iterate from 1 to n.For dp[i][j], there are two possibilities:
1.We will get the minimum substring without removing S[j], it is equivalent to such a fact that there is a number m which is 0 or a single bit of(j-i) satisfies dp[i-1][j-m-1]=min(dp[i-1][i-1],dp[i-1][i],dp[i-1][i+1],...,dp[i-1][n]).In this way dp[i][j]=S[j].
2.If we have to remove S[j] to get the minimum substring, it produces following dp transition : dp[i][j]=min(dp[i][j-m1], dp[i][j-m2],...,dp[i][j-mt]), m1,m2,...,mt is the single bit of (j-i).
I believe that the first solution could be optimized to $$$O(n^2\log^2{n})$$$ since for each state in $$$dp[m][mask]$$$ we need to store only positions of $$$O(\log n)$$$ segments.
My Approch and solution for problem C.
Link