Привет всем. На этой неделе (8-12 января 2018 года) проходит областная олимпиада по информатике в Беларуси. Олимпиада проходит во всех областях (а их у нас всего шесть) в одно и то же время с одним и тем же набором задач. Здесь можно обсудить олимпиаду, ознакомиться с уловиями задач (надеюсь, что все участники олимпиады ознакомятся с условиями на самой олимпиаде) и, может быть, если я смогу решить, с решениями.
Всем участникам желаю удачи!
Условия и решения задач для каждого из туров появятся не раньше их завершения.
Первый тур
Задача 1. Два квадрата
Решение
Задача 2. Творческие выходные
Подсказка 1
Решение
Задача 3. Непростая сумма
Подсказка 1
Подсказка 2
Подсказка 3
Решение
Задача 4. Роборалли
Подсказка 1
Подсказка 2
Подсказка 3
Решение
Второй тур
Задача 1.
Решение
Задача 2.
Решение
Задача 3.
Подсказка 1
Подсказка 2
Подсказка 3
Решение
Задача 4.
Подсказка 1



 .
.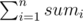 , где
, где 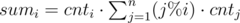 , a
, a 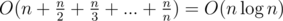 на вычисление ответа.
на вычисление ответа. .
.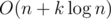 .
.






Условия первого тура здесь
Условия второго тура здесь
Результаты Витебской области.
Результаты Витебской области
Качество
Результаты Брестской области: http://codeforces.me/blog/entry/57042 (ссылка больше не действительна)
Результаты Брестской области ниже
Брестская обл
Ещё одно решение задачи второго дня C.Фотокружок.
Если очень не хочется придумывать ДО специально для этой задачи, то можно свести её к более тривиальной.
Выпишем в новый массив разности соседних чисел, то есть A2 - A1, A3 - A2, ..., AN - AN - 1. Назовем этот массив B. Получив очередные Li и Ri, будем рассматривать отрезок в массиве B от Li до Ri - 1 (Li = Ri нужно рассмотреть отдельно и просто вывести 1). Не трудно понять, что ответ на вопрос задачи равен maxSeg + 1, где maxSeg — это сумма в массиве B на подотрезке отрезка [Li, Ri - 1] с максимальной суммой (То есть, если рассмотреть все подотрезки, границы которых лежат от Li до Ri - 1 и посчитать на них сумму, то maxSeg — это максимальная из таких сумм).
Нахождение на отрезке подотрезка с максимальной суммой является довольно тривиальной задачей, по крайней мере полезно о ней знать.
Будем использовать дерево отрезков. В вершине будем хранить 4 значения для отрезка — максимальную сумму на префиксе, максимальную сумму на суффиксе, максимальную сумму на подотрезке и сумму на всем отрезке (3 из этих значений помогут нам пересчитывать ответ). Научимся объединять две вершины в одну (для построения дерева и вычисления ответа). Здесь я просто приложу часть кода (т.к. не хочу всё это писать словами).
При определенной реализации (если не учитывать подотрезки длины 0) maxSeg может быть равно - 1, это стоит учесть при выводе ответа.
Результаты г. Минска здесь. Таблица не содержит баллы участников, не получивших награду, по требованию комитета по образованию.
Результаты Могилевской области.
del