i_am_eating_wa_and_tle's blog

Help needed.
By i_am_eating_wa_and_tle, 7 years ago, In English

Is it possible to find the last two non-zero digits of a factorial of a number ranges from 1 to (10^100)! ??????

  • Vote: I like it
  • +3
  • Vote: I do not like it

Comments Comments (7)
| Write comment?
»
7 years ago, # |
  Vote: I like it +5 Vote: I do not like it

It reminded me one of AMC problems which asks last 2 non-zero digits of 90!. Here you can find solution: https://artofproblemsolving.com/wiki/index.php?title=2010_AMC_12A_Problems/Problem_23

→ Reply
»
7 years ago, # |
← Rev. 5   Vote: I like it +1 Vote: I do not like it

First of all, sorry for my bad attempt at Latex.

Let's say you want to find the last two non-zero digits of n!. We want to be able to use modular arithmetic, so we need a way to get rid of the trailing zeroes. To do this, we express n! as 5k·m where m is not a multiple of 5. Now, we see that is n! without the trailing zeroes. Thus, we want to find .

To do this, we can split the product n! = 1·2·3···(n - 1)·n. Let . Thus, n! = (1·2···100)(101·102···200)···((n - r)(n - r + 1)···n). From this, we get . But, we need , not n!. To do this, we remove powers of 10 from r! and 100!, or in other words, calculate the last two nonzero digits of 100! and r!. This can be done using the trick in the link provided by an earlier comment: here.

Let T be the two-digit number representing the last two non-zero digits of 100! and let R be the two-digit number representing the last two non-zero digits of r!. Then, the final answer is , which can be done quickly in 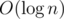using fast exponentiation.

Now, you are asking for up to "10^100!", and I'm not sure if that is a factorial sign or an exclamation point. If you, in fact, meant "10100!" rather than "10100!", then this algorithm is too slow, but it should take care of up to about 10300, 000.

If you did mean 10100!, just reading in the number will take so much time that the Sun would not exist anymore.

→ Reply
»
7 years ago, # |
  Vote: I like it -13 Vote: I do not like it

Yes you can by iterating 100 iterations because after that it would be two zeros ...

Proof is that you want that number module 100 so after 100 iteration definetly there is one number that divides 100 so its module gonna be 0 which means you don't have to continue multiplying because the result will stay 0 and the answer is 00 ... so if the number is under 100 you have to compute the answer ... other wise its 00

→ Reply