BledDest's blog

Educational Codeforces Round 35 — Editorial
By BledDest, history, 7 years ago, translation, In English
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
  • Vote: I like it
  • +38
  • Vote: I do not like it

Comments Comments (37)
| Write comment?
»
7 years ago, # |
  Vote: I like it +11 Vote: I do not like it

Btw, O(N^2) solution (even without bitmasks) for problem G.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I couldn't understand your solution by reading the code :/ Would you please explain your solution?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +5 Vote: I do not like it

      It's just like: for (int i = l; i <= r; ++i) if (a[i] == x) a[i] = y;, but is written a bit trickier.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +37 Vote: I do not like it

        Well if you thought that that solution got accepted is a bad thing... look at this: http://codeforces.me/contest/911/submission/33820899

        the most naive solution can get accepted with some tricks..

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it +5 Vote: I do not like it

          Hi, can you tell us what does this "unroll-loops" pragma mean and what does it do?

          → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it +5 Vote: I do not like it

          Yes. Please throw some light on the 3 pragmas mentioned.

          → Reply
          • »
            »
            »
            »
            »
            »
            7 years ago, # ^ |
              Vote: I like it +5 Vote: I do not like it

            the first just tells the compiler to optimize the code for speed to make is as fast as possible (and not look for space)

            the second tells the compiler to unroll loops. normally if we have a loop there is a ++i instruction somewhere. We normally dont care because code inside the loop requires much more time but in this case there is only one instruction inside the loop so we want the compiler to optimize this.

            and last but not least we want to tell the compiler that our cpu has simd instructions and allow him to vectorize our code

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              7 years ago, # ^ |
                Vote: I like it 0 Vote: I do not like it

              Interesting! Did you tried experimenting their combinations and see how each pragma affects the time? Just curious.

              → Reply
              • »
                »
                »
                »
                »
                »
                »
                »
                7 years ago, # ^ |
                  Vote: I like it 0 Vote: I do not like it

                they are all required to pass the tests

                → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it +4 Vote: I do not like it

          Can you suggest where I can learn about using pragmas?

          → Reply
          • »
            »
            »
            »
            »
            »
            7 years ago, # ^ |
              Vote: I like it +3 Vote: I do not like it

            i am sorry i have no source for this... but in generel i would recomend not to use them anyway! This solution was definitely not wanted and should never have passed... and normaly it doesn't help to use any pragma to get accepted. You just need to find a good algorithm. (some of this pragmas make normal code slower!)

            → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Haha, manual loop-unrolling ftw.

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it -10 Vote: I do not like it

    Anyway, your solution uses segment tree idea under the hood, right?

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    Can you give some suggestions on how to make the program run faster if there is something more than just simple loops(for example,dfs and so on)?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +17 Vote: I do not like it

      You know, if we talk about the general case, then there is an acceleration operator in c++. For example:

          here_is_some_code_that_takes_much_time();

      Now use acceleration operator:

          // here_is_some_code_that_takes_much_time();

      Bingo! Now you code runs very fast.

      But seriously, I have some ideas for optimizing solutions with graphs, but so far there has not been a problem where I could test them =) Well, the general suggestions are simple: do as few operations as possible and access to memory as fast as possible.

      → Reply
»
7 years ago, # |
  Vote: I like it +16 Vote: I do not like it

Here's a nice implementation for E that I wrote after the contest: 33746048.

→ Reply
»
7 years ago, # |
  Vote: I like it +9 Vote: I do not like it

Problem G can be solved in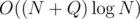 independent of max ai.

For each value, we store the positions it occurs in. This can be encoded into a segment tree-like data structure, where we have a node for each range (that would be in a regular segment tree) that contains the value at least once. There will be nodes total.

To change x to y in a range, first divide it into intervals that are represented by single nodes (like in a regular segment tree). Then, merge each node for x into the corresponding node for y. If either is empty, we at most do a swap, which is O(1). Otherwise, we recursively merge the children and delete the original x node. We may also add new nodes on the paths back to the root.

The answer can be recovered by recursively traversing the data structure for each number.

The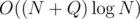 time bound can be shown using amortized analysis with the potential function as the number of nodes.

Here is my (after contest) implementation of this approach.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Can you elaborate more on the proof of complexity?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +3 Vote: I do not like it

      To make it easier to explain, I'll be referring to my implementation.

      Building the data structure and recovering the answer are clearly .

      nodes are created at the beginning and at most nodes are created during each query. Therefore, only nodes are created overall.

      If a > L or b < R, "transfer" divides the interval the same way a top-down segment tree does. This takes per query.

      If a ≤ L and b ≥ R, "transfer" will always delete a node. Since only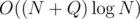 nodes are created, this can only happen 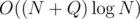times. The body of the function excluding recursive calls (which are counted separately) takes O(1), so its total runtime is .

      → Reply
»
7 years ago, # |
  Vote: I like it +10 Vote: I do not like it

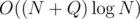911D - Inversion Counting can be solved with help of Cycle Decomposition in O(n+m). We can find the parity of the initial permutation in O(n) in this way, reducing the overall complexity to O(n+m). Link to My Submission

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it -8 Vote: I do not like it

    but this while increase the complexity of the algorithm """while(!vis[now]) {vis[now]=1; now=P[now];}""" i wrote a code using BIT wich take O(nlog(n)) to find the initial permutaion, and it take the same time as you '109ms'

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      The time complexity of finding initial no of inversions is still O(n). There are two nested loops, but they are not executed for all values.

      Let's say, for loops begins with 1, and then while loops runs till n, so it will mark all elements from index[1,n] as visited and hence while loop will not be executed for those values again.

      One can visualize it as; for loop is executing while loop for element at given index i, if it is not marked, whereas while loop marks element which is present at index of given element.

      For any i, we have three case P[i]=i, P[i]<i and P[i]>i.

      if P[i]=i, while loop runs only once i.e. marks that element

      if P[i]<i, since for loop has already been executed till i, P[i] is already marked, so no execution of while loop

      if P[i]>i, while loop marks element P[i], and hence will not be executed when i=P[i]

      → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In G i have used sqrt decomposition and in each block i maintained the fact that the current element refer to which element now (As doing this brutely takes O(100^2) I have used two long long integers and then with normal bitwise operations i maintained this. Thanks for such a nice problemset :)

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

If possible can anyone please give the question links similar to F!

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone give me an example of author's solutuion of problem G, please?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    just look at 33740346 by pannibal

    very beautiful~

    → Reply
    • »
      »
      »
      4 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      I don't get how to update parent's node using children. Can you please explain what does that mean : seg[x][i] = seg[rs][seg[ls][i]];

      upd: got it. just remember that segment tree is built on queries, not elements. we want to merge 2 sons. we consider that left son and right son both influence value of current scanline index. answer for value firstly changes in left son, then the result is changing in right son, that is why we have seg[x][i] = seg[rs][seg[ls][i]];

      → Reply
»
7 years ago, # |
  Vote: I like it +6 Vote: I do not like it

We can also prove D like this: If we reverse segment [l, r], then all inversions (i,j) which i < l or j > r will not be affected, so we just consider the number of inversions (i, j) which l <= i < j <= r. Let a is the number of inversions (i, j) which l <= i < j <= r, and b is number of all pair (i, j) which l <= i < j <= r, so b = (r — l + 1) * (r — l) / 2. Then if you reverse segment [l, r], a will change to b — a (all pairs which are not inversions will change to inversions, and vise versa). And because we just consider the parity of the result, we can change b — a to b + a. So that mean you just need to consider about the parity of b.

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In problem C, why answer for 4 3 2 is NO ? x1=1,x2=4,x3=2 will not lead to "YES" ?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    there are many counter cases. One of them is 303 (as 4 and 3 only lead to odd places in this case but neither 302 is divisible by 4 nor 299 by 3).

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    inp: 4 3 2

    x[] = 1 4 2

    1 5 9 13 ...

    4 7 10 13 ...

    2 4 6 8 10 12 14 ...

    from 4, there is no 11.

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

can somebody elaborately explain problem D ?

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 3   Vote: I like it +3 Vote: I do not like it

    As the editorial says: “permutation with one swap is called transposition”. So, intuitively, you can think of a transposition as being a single swap. For example, one could say '[2, 1, 4, 3] is one transposition 'away' from [1, 2, 4, 3]', as only one swap (transposition) has been carried out.

    Think of the identity permutation as a permutation in ascending order (so no inversions). For example, [1, 2, 3, 4, 5, 6] is the identity permutation of length 6 and [1, 2, 3, 4, 5, 6, 7, 8] is the identity permutation of length 8.

    The parity of the permutation equals the parity of the number of transpositions needed to get it from the identity permutation. Parity is whether something is even or odd. For example, [4, 1, 2, 3, 6, 5] has even parity as there are four transpositions needed to get it from the identity permutation ([1, 2, 3, 4, 5, 6]). Swap elements with indices 1 and 4, then with indices 4 and 3, then indices 3 and 2, then indices 5 and 6.

    The parity of the number of inversions = parity of the permutation.

    So, the algorithm proposed by the editorial involves first calculating the number of inversions in the initial permutation. This can be done “naively (check all pairs of indices)”. For example, if we have [3, 2, 4, 1], first compare 2 and 3 (INVERSION!), then compare 4 and 3, then 4 and 2, then 1 and 3 (INVERSION!), then 1 and 2 (INVERSION!) and finally 1 and 4 (INVERSION!). So we have four inversions, so parity of inversions before any reverses is even.

    Then, for each reverse you carry out, count the number of swaps in whatever way you want (the editorial suggests one way). Let's say the permutation before the reverse has x transpositions from the identity permutation and we know the parity of x (not necessary to know x itself). Let's call the number of swaps carried out in a single reverse y. The parity after the reverse = parity of x+y, as x+y is the total number of transpositions that have been carried out on the identity permutation to get to the current reversed permutation. If y is even, then parity after reverse = parity before reverse. If y is odd, the parity switches after reversing. (consider all the different possible parities of x and y). Thus, we can work out the parity of the permutation after ever reverse query.

    You can also do this problem using cycle decomposition, which is what was suggested earlier (http://codeforces.me/blog/entry/56771?#comment-404553). If you're interested, you can read online about parity of permutations, cycles, transpositions, etc.

    Hope that helped!

    → Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

B can be done in O(log n).

→ Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

kudos to the author of problem D !!!!

→ Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Alternate solution for G : We can use DSU with blocks division to solve the problem. Using DSU, we can find the final color of each initial color. We can maintain a groups array for the group of the current color and the parent array to find the current set of groups merged with the original color in DSU. Update is pretty straightforward with block updates of size sqrt(N). Time complexity will be O(Q*(100 + sqrt(N))).

→ Reply