909A - Генерация логина
Самое простое решение — сгенерировать все возможные логины (перебрав все пары непустых префиксов имени и фамилии и скомбинировав их) и выбрать из них первый по алфавиту.
Более быстрое решение основано на следующих свойствах логина. Во-первых, в первом по алфавиту логине префикс фамилии всегда состоит ровно из одной буквы (если префикс фамилии содержит две или более буквы, удаление последней буквы префикса позволяет получить логин, расположенный раньше в алфавитном порядке). Во-вторых, префикс имени не должен содержать букв, больших или равных первой букве фамилии (за исключением первой буквы имени), из аналогичных соображений.
Эти свойства дают жадное решение: будем перебирать буквы имени, начиная со второй. Как только найдена буква, большая или равная первой букве фамилии, возвращаем префикс имени до этой буквы (не включая ее) плюс первую букву фамилии. Если таких букв нет, возвращаем все имя плюс первую букву фамилии.
909B - Отрезки
Рассмотрим участок координатной прямой [i, i + 1]. Очевидно, все отрезки, покрывающие этот участок, должны находиться в разных слоях. Для каждого из этих отрезков левый конец находится в одной из точек 0, 1, ..., i (i + 1 вариантов), а правый — в одной из точек i + 1, i + 2, ..., N (N - i вариантов). Итого отрезков, покрывающих участок [i, i + 1], будет Mi = (i + 1)(N - i) штук. Наибольшая из величин Mi для i = 0, ..., N - 1 даст нам оценку снизу для необходимого количества слоев.
Задача не требует разбиения отрезков на слои в явном виде, поэтому можно предположить, что эта оценка снизу — точная. max Mi можно найти за O(N), или можно заметить, что максимум достигается для 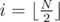 (для центрального отрезка, если N нечетное, или одного из двух центральных, если N четное).
(для центрального отрезка, если N нечетное, или одного из двух центральных, если N четное).
Ответ — 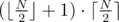 .
.
Этот же ответ можно получить явным построением. Отсортируем отрезки в порядке неубывания их левых концов и затем в порядке возрастания их правых концов. Будем распределять отрезки по слоям жадно: если i — левый конец текущего отрезка, и участок [i, i + 1] свободен в каком-то слое, добавим текущий отрезок к этому слою; иначе начнем новый слой с этим отрезком.
и да, это наша задача с решением за O(1) :-)
909C - Отступы в Python
Эту задачу можно решить при помощи динамического программирования.
Рассмотрим все возможные программы, которые заканчиваются инструкцией i, записанной с отступом j. Обозначим количество таких программ dp[i][j].
Для первой инструкции dp[0][0] = 1, dp[0][j] = 0 для j > 0 (есть ровно одна программа, состоящая из одной инструкции, и она записана с нулевым отступом).
Рекуррентное соотношение для перехода к следующей инструкции в программе следует из описания инструкций: когда мы добавляем инструкцию i + 1, возможные значения отступа для нее зависят от возможных значений отступа инструкции i и от типа инструкции i. Если инструкция i — цикл, инструкция i + 1 должна иметь отступ на один больше предыдущей, поэтому dp[i + 1][0] = 0 и dp[i + 1][j] = dp[i][j - 1] для j > 0. Если инструкция i — простая инструкция, то команда i + 1 может быть частью тела любого из предшествующих циклов, и иметь любой отступ от 0 до отступа инструкции i. Если мы обозначим отступ инструкции i (простой инструкции) как k, отступ инструкции i + 1 как j, нам нужно просуммировать все случаи, для которых k ≥ j: 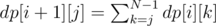 .
.
Итоговый ответ будет общим количеством программ, заканчивающихся последней инструкцией с любым отступом: 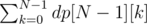 .
.
Сложность решения — O(N2).
909D - Разноцветные точки
Непосредственная реализация действий, описанных в задаче, с перебором всех точек для определения того, какие из них удалять, имеет сложность O(N2) и занимает слишком много времени.
Рассмотрим непрерывные группы точек одинаковых цветов. Одно действие удалит только точки на границах группы (за исключением точек на левой границе самой левой группы и правой границе самой правой группы, если в этих группах больше одной точки), остальные точки будут не затронуты. Если текущие размеры групп слева направо N1, N2, ..., NG - 1, NG, то размеры групп после выполнения первого действия — N1 - 1, N2 - 2, ..., NG - 1 - 2, NG - 1, после выполнения второго — N1 - 2, N2 - 4, ..., NG - 1 - 4, NG - 2 и т.д. Этот процесс продолжается до тех пор, пока одна из групп не исчезнет, после этого ее соседние группы могут объединиться, если они одного цвета.
Это наблюдение позволяет симулировать несколько действий за одну итерацию:
Найти количество действий, необходимых для того, чтобы хотя бы одна группа исчезла.
Пересчитать размеры групп после этого количества действий.
Удалить пустые группы.
Объединить соседние группы одного цвета.
Такая итерация требует O(G) времени и удаляет O(G) точек (не менее одной точки из каждой из G групп). Если начальное количество точек было N, мы можем удалить не более N точек. Таким образом, сложность этого решения — O(N).
909E - Сопроцессор
Действовать следует жадно: пока есть задачи, которые могут быть выполнены на главном процессоре сейчас (т.е. все задачи, от которых они зависят, уже выполнены), их следует выполнять; затем следует переключиться на сопроцессор и выполнять все задачи, которые могут быть выполнены на нем; затем переключиться обратно на главный процессор и т.д. Это можно сделать при помощи аккуратно реализованного поиска в ширину. Один из вариантов реализации — вместо того, чтобы на каждом шаге искать доступные задачи, их следует хранить в двух очередях (задачи, доступные главному процессору и сопроцессору) и добавлять задачу в соответствующую очередь, как только все задачи, от которых она зависит, выполнены.
Существует также более формальное решение. Определим Ti как минимальное количество вызовов сопроцессора, необходимое для выполнения i-ой задачи, и выведем рекуррентное соотношение для Ti. Если u — задачи и v1, ..., vk — ее зависимости, очевидно для каждого i Tu ≥ Tvi (потому что u должна выполняться после vi). Затем, если vi выполняется на главном процессоре, а u — на сопроцессоре, то выполнение u потребует дополнительного вызова сопроцессора. Таким образом, Tu = maxi(Tvi + si), где si = 1, если u выполняется на сопроцессоре и vi — на главном процессоре; иначе, si = 0. Теперь все Ti можно вычислить при помощи рекурсивного обхода графа зависимостей (или обхода задач в топологическом порядке). Ответ — max Ti.
909F - И-перестановки
Перестановка p (pi & i = 0)
Если N нечетно, ответ NO. Действительно, любое число в позиции с нечетным номером i pi должно быть четно (в противном случае последний бит pi&i равен 1). Для нечетных N четных чисел меньше, чем позиций с нечетным номером, поэтому в какой-то из позиций окажется нечетное число, следовательно, сконструировать нужную перестановку невозможно.
Если N четно, ответ YES. Чтобы построить нужную перестановку, заметим, что (2k - i)&(2k + i - 1) = 0. Например, для k = 5:
100000 = 25
011111 = 25 - 1
100001 = 25 + 1
011110 = 25 - 2
и так далее.
Мы можем использовать это наблюдение, чтобы составлять пары из чисел 2k - i и 2k + i - 1, то есть выбирать p2k - i = 2k + i - 1 и p2k + i - 1 = 2k - i.
Полная процедура построения нужной перестановки следующая. Для заданного четного N, найдем максимальную степень двойки, не превышающую N, 2k. Составим пары из чисел 2k - i и 2k + i - 1 для всех i = 1..N - 2k + 1. Если после этого остались еще неиспользованные числа, это будут числа от 1 до 2k - (N - 2k + 1) - 1 = 2k + 1 - N - 2. Повторим процесс для N' = 2k + 1 - N - 2.
Рассмотрим процесс на примере N = 18. На первом шаге мы выбираем 2k = 16 и составляем пары из чисел 15-16, 14-17 и 13-18. На втором шаге неиспользованными остаются числа от 1 до 12, мы выбираем 2k = 8 и составляем пары 7-8, 6-9, 5-10, 4-11 и 3-12. На третьем и последнем шаге неиспользованными остаются числа 1 и 2, мы выбираем 2k = 2 и составляем пару из чисел 1 и 2. После этого все числа использованы, и перестановка построена.
Перестановка q (qi & i ≠ 0)
Для N = 1..7 мы можем рассмотреть все перестановки вручную и выяснить, что для N = 1..5 ответ NO, для N = 6 возможная перестановка \textbf{3 6 2 5 1 4} (из примера в условии), и для N = 7 возможная перестановка \textbf{7 3 6 5 1 2 4}.
Если N — степень двойки, ее двоичное представление 10..0. По условию qN ≠ N, поээтому qN < N, и двоичное представление qN короче, чем двоичное представление N. Следовательно, qN&N = 0, и ответ в этом случае NO.
Наконец, если N > 7 и N — не степень двойки, нужная перестановка всегда существует, и ее можно построить следующим образом. Разобьем все числа от 1 до N на следующие группы (k — наибольшая степень двойки, которая все еще меньше N):
1..7
8..15
16..31
\ldots
2k - 1..2k - 1
2k..N
Для первой группы используем перестановку, которую мы нашли вручную для N = 7. Для остальных групп используем произвольную перестановку чисел в этой группе (например, циклическую перестановку). Числа в каждой группе, кроме первой, имеют общий ненулевой бит в одной и той же позиции (соответствующей степени двойки, с которой начинается группа) поэтому qi&i гарантированно имеет ненулевой бит в этой же позиции.











Woaaaaahhhh..Lightning fast editorial. Amazing. :)
This is the first contest ever in which I wrote editorials together with the problems, so they were ready even before the start of the round :-)
I always wonder that why all the problem setters don't do it this way in every contest?
I mean.. it will be so nice for both the parties. Not only we (the noob coders) will get editorials instantly but it might help the setter sometimes to get to know a mistake (if there is in a problem) while writing its solution. This will reduce the chances of a round getting unrated.
Anyways..you have done a great job.. One of the best contests on codeforces. Congrats for this. :)
Hi, can you provide code for problem D , it looks like a lengthy implementation , the algorithm was not very hard to come up with, also , love the B problem , felt it was a O(1) problem and I was not disappointed :)
Nice Nickolas <3
My solution of D: https://paste.debian.net/1002718/
As always, solution for a problem is quite easy but why I can't come up with it..
Anyway, thanks for great problems!
Really interesting problems, thanks! I wish I could solve the F, the solution was near but my brain was making circles around it so I didn't reach it.
Greedy simulation for problem B got AC
Did anyone solve D by another method : making a right arrays which stores the logical next element and making a left array which stores the logical previous element in array and then performing logical deletion by changing the left and right array values. Eg. _ a a b b_ _ left[i] {-1 , 0 , 1 , 2} ........._ _ right[i]{ 1, 2, 3, 4}_ .................... after one operation , left[i] becomes {-1,X,X,0} and right[i] becomes {3,X,X,4} and so on (by proper implementation procedure taking case of indices etc) and then count total number of steps(again proper implementation required). If anyone solved like this , please provide your code .
I solved that way, but we still need to "compress" the string or it will lead to TLE (my first submission made me realize it).
My code is not a beautiful thing, considering my hurry during the contest, but I've added some comments trying to help. http://codeforces.me/contest/909/submission/33698415
Thanks for the nice problems. Can you help me why recursive top down solution is failing on time on this solution?Link Is the constant time factor of creating recursion stacks that much?
well , time limit is a little strict honestly (not saying badly formed) , on top of that you are using java + recursion.. also memory is also O(n*n) which I think slows it down a bit more... It would have been better if n <= 3000 , the problem would still remain the same but some failed solutions would have passed ,
You have O(N2) dp states, and for one state you are doing O(N) operations here:
That makes your solution O(N3), so no surprise it is TL.
You have to get rid of that bad cycle and use prefix sums to get the value in O(1).
Thanks for providing editorial right after the contest!
I was hoping to find some magical connection between two unrelated subproblems from F at least here, but it seems that there is indeed no connection :)
Something quite similar to (A&B==0) subproblem appeared as a problem at CF in past: 288C - Polo the Penguin and XOR operation. Today I got a construction algorithm which sounds a bit different from editorial (I didn't check, maybe it gives same permutations as one from the editorial and I just approached it from the other end). Here is the code: 33686199, function run_solver_false is what we are looking for :) And below I'll try to give some explanation on what's going on there.
Let's take a permutation 2 1 4 3 6 5 8 7 10 9... first, to resolve last bit and p[i]!=i statement. Now let's fix bits one by one from lower to higher. In order to fix a bit X, let's take all positions for which this bit is broken and make a swap of p[i] and p[i-(1<<X)]. We know that (i-(1<<X)) will have 0 at position X, so we are not going to break stuff at that position — but we are still afraid that the number we'll get from p[i-(1<<X)] has 1 at position X as well.
One can check that it is not the case: in each block of size (1<<X) which we consider as a candidate for making a fix there is exactly one number with bad bit, and this number will always stay at second to last position in the block — we will put it there when constructing our base permutation, and then when considering a move at level X (which can possibly affect this number) number in the block to the right will be OK — it will be "bad number" of level X+1. For example: the only moment we can move 4 from position 3 is when trying to fix position 7, but we know that there will be 8 there and it will not need a fix. Generalizing it, the only bad number in block ends with 1000...00 (X times 0), and it will stay at place because the number ending with 1000...00 (X+1 times 0) to the right from it will not need a fix.
Could someone explain the solution to problem C. What is the dp array actually storing?
dp array is storing the ways in which a level of indentation can be reached at the n-th instruction.
for example, lets start with the first line, the indentation level has to be lowest so the array will look like
1 0 0 0 0 ... 0 (n-1 times 0)
if it is a for instruction the possible indentation levels when the next instruction is received can only be '1' tab or '1' space. so the indentation can only be equal to '1', ie.
0 1 0 0 0 0 0 ... 0 ( n — 2 times 0 )
and similarly
and what is the logic behind other dp states??
Any dp[i][j] represents the ways in which the program can be written with the first i+1 instructions with last line having indentation level of j.
This holds for i = 0 Since the indentation can only be zero on the first line in one way.
This holds for any i by inductive reasoning. (You can verify this from the algorithm in the editorial. slycelote has also suggested a correction, please take it into account too)
So it holds at the n-th instruction. So dp[n-1][j] represents ways of writing the program with first n instructions with indentation equal to j.
As the indentation can vary from 0 to n we must add up all the terms do[n-1][j] as the program can end with any indentation level.
Hope this explained the problem
I wrote a blog for you click here
Sir, thank you for this excellent article. Without you I would not have been able to understand the solution of this problem
can someone prove that the lower bound we find in problem B is really the smallest number of layers ?
Well for the lower bound to be the smallest number we would need to prove that we can construct each layer such that each segment that covers the maximally covered area [i,i+1] is a part of each layer.
First off, note that the maximally covered segment is in the middle as a segment [i,i+1] is covered by (i+1)*(n-i) segments (taking one starting point <=i and ending point >=i+1). (There are two such areas when n is even)
Then we can construct a solution: starting from i=0 take any segment starting at i, and ending at n-i, and split that segment at some point. One of the segments will cover the maximally covered area. Repeat this for all such split points. increment i, repeat.
It is clear that every layer includes a unique segment that covers the maximally covered area, and every segment is included in one layer. Thus, as every layer includes a unique segment that covers the maximally covered area, the number of layers is the same as the number of unique segments that cover the maximal area, aka the lower bound. So the lower bound is the smallest number of layers.
If you think of the construction procedure in the editorial, you'll realize that the only time we add a new layer is when current segment [i, i + 1] is occupied in each of the existing layers. And that's exactly what the lower bound argument used.
An Elegant Sol to B :
Ref
Surely not as elegant as the O(1) solution!
Что не так в моем решении 909D - Разноцветные точки [](http://codeforces.me/contest/909/submission/33697890)
В unite() возможно, что
v[i].second<=0для всех i.B — Segment in Haskell
`
In Java
In C how time complexity is O(N*N)?
U can use prefix sum to calculate the summation instead, hence reducing the complexity from O(n*n*n) to O(n*n).
In problem (C — Python Indentation) output for the following input is 23. But how? I don't get it.
Задача С. Пронумеруем позиции в строке слева направо и будем в массиве А хранить количество вариантов программы, начинающихся на данном шаге написания программы с данной позиции. Рассмотрим очередной шаг написания программы. Если предыдущая команда "f", то следующая команда пишется со сдвигом на одну позицию вправо, т.е. количество вариантов, в которых последняя строка начинается в позиции 1 равно нулю, в позиции 2 — равно числу вариантов в позиции 1 на предыдущем шаге, в позиции 3 — в позиции 2 и т.д. Для всех i имеем A[i]:=A[i-1]. Если предыдущая команда "s", то следующая команда пишется либо в ту же позицию, либо в ЛЮБУЮ позицию левее, т.е. в данном случае для всех i A[i]:=A[i]+A[i+1]+A[i+2]+ ... и т.д. до последней возможной позиции начала первой строки на предыдущем шаге. После выполнения всех шагов написания программы нужно найти сумму вариантов для всех позиций начала последней строки. После написания первой строки A[1]=1, все остальные члены массива равны нулю. Далее N-1 раз повторяем описанный алгоритм нахождения числа вариантов начала последней строки в каждой из позиций. При чтении условия возникает впечатление, что соседние строки не могут начинаться с позиций, номера которых отличаются на количество отступов больше одного, т.к. в тексте задачи явно не сказано, что после завершения цикла следующая инструкция может начинаться с любой позиции с меньшим количеством отступов. К сожалению, приведённые примеры не позволяют избавится от такого заблуждения.
You can use this test case to debug your code:
In problem C, in the first input testcase given, the dp matrix formed by the given editorial will be : 1 0 0 0 1 1 1 1 0 1 1 1 0 0 1 1 and the final answer will be 2 but the answer in this case is 1. Can you please explain what am I missing here. Link to my code
Looks like the editorial has a typo, the actual recurrent formula is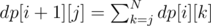 .
.
slycelote Thank you for correcting the typo. Please also provide some details about how we derived this recurrence if ith command is a simple statement.
As pointed out in the editorial, indentation of the command following the simple statement must be less than or equal to indentation of the simple statement. In the formula above, k is indentation of the simple statement, j is indentation of the next statement, and we sum over all k such as j ≤ k.
[user:sukhbhir947] Lets say you put the i+1th command with indentation k, then the ith command can only be with indetation k or k+1 or k+2 or .... n. So the number of ways of putting the command i+1 with indentation k will the sum of all the ways you can put the ith command with indentation k, k+1, k+2 ... n.
Hope it helps!
Thanks a lot!
Hello all, I need some help in understanding problem C's editorial. If ith command in the program is a simple statement then how did we derived the recurrence relation for i+1 th command.
if ith one is simple then no matter what is the current command we can indent it in any of the statements before the last indentation of ith command(maximum indent).
see if fffs then we are about to add f. As the maximum indentation of previous command (i.e. s) is 4 so, we can put the current f in any of the for loops or with that s!
Hope it helps.
for DIV-D : i didn't understand the time complexity part. We have G groups and at each step we remove 1 group and then update the remaining one. so, updating takes O(G-1) time (if we do linearly). so, complexity will be about O(G^2) ! I think that the size of groups reduces at each step and possibly that is the point i am missing. But can someone please provide any mathematical stuffs. will be a great help! :)
AND thanks for such a nice tutorial happy new year :)
Time complexity will be the sum of O(G) over all operations. At the same time, the total number of points removed will be at least the sum of G over all operations because for each operation we remove at least one point from each group. We cannot remove more than N points in total, so this sum is not more than N, and the sum of O(G) is not more than O(N).
Hey all Can someone please tell me the detailed solution of problem C (Python Indentation) I approached the question as a)if there are two 'for' statements (not consecutively) the total number of possibilities get multiplied by 2
b)if there are n 'simple' statements(consecutively) inside a 'for' loop then total number of possibilities increase by n-1 Please tell me my blunders in my approach.
can someone please explain the second approach mentioned in the editorial of E.
Do you have a specific question?
For Problem C Python indentation why is the final answer the sum of (j takes on all levels) dp[n-1][j],and where is the running variable k in the summation used?.(k=0 to N-1) Thanks!.
This is another typo. Sum is over all possible indents of the last command k, and dp[N - 1][k] is the number of programs which end with command N - 1 at indent k.
In the tutorial of the 909C-Python Indentation it's given that: "If command i is a simple statement, command i + 1 can belong to the body of any loop before it, and have any indent from 0 to the indent of command i:" But then the formula sums from i=j to n. Shouldn't it be from 0 to j?
If command i is a simple statement, indentation of command i + 1 must be less than or equal to indentation of command i. In the formula, k is indentation of command i + 1, j is indentation of command i + 1, and we sum over all k for which j ≤ k — this requires summing upwards from j, not downwards.
Thanks for the explanation. Appreciate that.
There is a slightly slower solution to D that will AC.
It is essentially an optimized simulation; we don't need to check the neighbors of every point, only the points that get new neighbors. Which are the points that get new neighbors? Well, these are just the points adjacent to the removed points (be careful not to mark a removed point as having a new neighbor).
We'll keep three sets: one with all the points, one with the points that have new neighbors (we'll actually need a current and a next for this set, and then use pointer swapping, but it's easy to think of it as just one set), and one with the points you are going to remove. On each iteration of the simulation, check if the points with new neighbors need to be removed, and add them to the remove set. Then, add their neighbors to the "has new neighbors" set. When you iterate over the "remove" set, just make sure you delete any of those elements from the "has new neighbors" set.
Each element can be removed at most O(1) times, and each of its neighbors will be added to the "has new neighbors" set, so there are at most n insertions to that set, and of course n deletions as well, so the amortized complexity is O(n logn).
Your solution is definitely easier to implement, but I think in some cases this might be easier to think of.
Can someone explain for Problem D:
Answer for input: bccdeefggiaacndddd
should be 2.
But according to solutions it is : 1
My solution for 2 is : (bc)(cd)(e(ef)g)(gi)(a(ac)n)dddd
Why should it be 2? Each point, except for the last 3 "d"s, has a neighbor of a different color and thus will be removed during the first operation; after that the points will be "ddd" and none of them have a neighbor of a different color, so second operation can't be done. Points do not have to be paired up to be removed
My bad!! Understood problem statement now.
Thanks :)
Here's an alternate construction for the second part of F. Assume we want a solution for some value of n that is greater than 6 and not a power of two.
If we have a solution for n - 1. We just find a power of 2 say 2p less than n such that n contains a 2p in its binary representation. Then we construct a solution for n by assigning the 2p in our previous solution a value of n and n the value that 2p had before the reassignment. We leave everything else the same.
Next if we don't have a solution for n - 1, but we do have a solution for n - 2 (i.e in the the case n - 1 is a power of 2). We just take our solution for n - 2 and put {n, n - 1} on the end and we have a solution for n.
Then we just use this process to construct a solution using the solution for n = 6 in the example.
For problem D , I use the set to maintain the remaining indexes which can be operate,but i got TLE on test 5. (:
I have a slightly different solution to problem D.
After making groups, we can observe that the simulation process cannot take more than $$$sqrt(n)$$$ "steps", because at each "step", we remove all values with equal ceiling function divided by two value, and the number of edge removals are bounded above by $$$logn$$$ "steps", so the overall complexity is $$$O(n(sqrt(n)+log(n))$$$ which is around $$$7*10^8$$$ operations for $$$n==10^6$$$, which passes in $$$33$$$ milliseconds.