Дано 4 массива A, P и B, Q размеров N и M запросов. Изначально, элементы A и B равны 0, и элементы P и Q отсортированы в неубывающем порядке и имеют ограничения 0 ≤ x ≤ 109.
Существует 3 типа операций:
- 0 ≤ x ≤ 109; 1 ≤ i ≤ N; Ai = x
- 0 ≤ x ≤ 109; 1 ≤ i ≤ N; Bi = x
- 0 ≤ x ≤ 109; 1 ≤ y ≤ 1018; Найти минимальное i, такое что выполняется
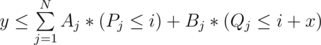
Существует простое решение, работающее за O(Nlog2N): хранить A и B в дереве Фенвика, когда нужно ответить на запрос, сделать бинарный поиск по i, и проверить, выполняется ли неравенство. Я хочу выяснить, существует ли решение за O(NlogN). Помогите с решением этой проблемы.











What does Qj ≤ i + x mean? Is its value 0 or 1 or what?
Can we assume that N and M are similar (e.g. equal)? You require some particular complexity that says nothing about M.
(x ≤ y) 0 or 1 if it's false or true, respectively. N and M are similiar. So you can replace M with N in complexity.
It would be easy with one pair of arrays. Then we would have a single segment tree and we instead of binary search we should start in a root of the tree and go down, each time checking whether we should go to the left (if its subtree sum is >= y) or the right child. Is this part clear?
With x = 0 it would be the same for two trees — we would just move on them simultaneously.
Let's do it for any x now. We again simultaneously move in trees, starting from roots. Let's say the current node in the first tree represents an interval [a, b] and the current node in the second tree represents an interval [c, d]. Let's assume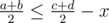 .
.
Nice approach! I need to think more about cases when solving problems.