never_giveup's blog

An interesting problem.
By never_giveup, 7 years ago, translation, In English

You are given 4 integer arrays A, P and B, Q of size N and M queries. Initially, elements of A and B are 0, and elements of P and Q are sorted in non-decreasing order and have constraints 0 ≤ x ≤ 109.

There are 3 types of queries:

  • 0 ≤ x ≤ 109; 1 ≤ i ≤ N; Ai = x
  • 0 ≤ x ≤ 109; 1 ≤ i ≤ N; Bi = x
  • 0 ≤ x ≤ 109; 1 ≤ y ≤ 1018; Find minimum i, such that

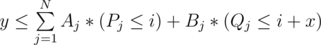
There is an easy solution with time complexity O(Nlog2N): store A and B in BIT, when you need to answer query, binary search by i, and check whether condition holds true. I'm looking for solution with time complexity O(NlogN). Any ideas about that?

  • Vote: I like it
  • +14
  • Vote: I do not like it

»
7 years ago, # |
  Vote: I like it +3 Vote: I do not like it

What does Qj ≤ i + x mean? Is its value 0 or 1 or what?

Can we assume that N and M are similar (e.g. equal)? You require some particular complexity that says nothing about M.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    (x ≤ y) 0 or 1 if it's false or true, respectively. N and M are similiar. So you can replace M with N in complexity.

    → Reply
»
7 years ago, # |
  Vote: I like it +46 Vote: I do not like it

It would be easy with one pair of arrays. Then we would have a single segment tree and we instead of binary search we should start in a root of the tree and go down, each time checking whether we should go to the left (if its subtree sum is >= y) or the right child. Is this part clear?

With x = 0 it would be the same for two trees — we would just move on them simultaneously.

Let's do it for any x now. We again simultaneously move in trees, starting from roots. Let's say the current node in the first tree represents an interval [a, b] and the current node in the second tree represents an interval [c, d]. Let's assume .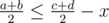

  1. If the sum in (stored in the left child of the current node in the first tree) is not smaller than y, move to that left child.
  2. The same for .
  3. If (the sum of sums in those two intervals) is smaller than y, move to the right child in the first tree, because the answer for sure won't be in interval .
  4. If is not smaller than y, move to the left child in the second tree, because the answer for sure won't be in .
→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    Nice approach! I need to think more about cases when solving problems.

    → Reply