Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 156 |
| 6 | adamant | 152 |
| 6 | djm03178 | 152 |
| 8 | Qingyu | 151 |
| 9 | luogu_official | 149 |
| 10 | awoo | 147 |
| Name |
|---|



In problem D
(n + (n - 1) - sum) / 2I think it should be
(n + (n - 1) - p) / 2Can you explain me why this formula works?
sorry, I do not understand how it works, I found this after reading other's code.
oo ok) but (n + (n - 1) - sum) / 2 100% not right... becuse it`s always 0
D. Why is there this weird result?
2 => 1
3 => 3
4 => 6
How is it possible to get 6 pairs?
http://codeforces.me/contest/899/submission/33360139
UPD: I did it because my last tests were not passed, for example
http://codeforces.me/contest/899/submission/33359341
The question asks for the number of pairs such that they produce the maximum number of trailing nines. When n < 5, there exists no pair such that their sum is a number with a trailing nine. Therefore we should print all pairs (as all of them produce the maximum number of trailing nines, which is zero). The number of pairs is simply nC2.
why not just output -1 or 0 when n<5...
Yes please. Someone explain D. or atleast how to come up with those ideas and the formulas.
The solution for D is fairly simple to come up with.
1) Observe that when n < 5, the answer is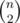 .
.
2) Observe that when n + (n - 1) is of the form 9....9 the answer is 1.
3) In all other cases, we need to iterate through the possible (i + j)'s that produce the maximum number of nines. So, say the maximum number of nines is x. Start at 9...9 (x times) and increment this to 1(9....9) (x times) 2(9....9) (x times) until we reach n + (n - 1). For each of these numbers we need to calculate how many pairs (i, j) sum up to them. Now, when the number is >= n + (n - 1), we need to add (number / 2) to our answer. This is because we can have: (number / 2) + (number / 2), (number / 2 + 1) + (number / 2 - 1) ...so on to sum up to the number. Otherwise if the number < n + (n - 1), we need to add (n - number / 2) to our answer. This is because we can have: (number / 2) + (number / 2), ..., n + (number - n).
Here's my submission for reference http://codeforces.me/contest/899/submission/33348429
It can be solved using digit DP. Submission Link Explanation
It should be
1 + (n + (n-1) - p)/2Pardon me for a stupid question.
In Div2B, the 13th test case is the following:
21 30 31 30 31 31 28 31 30 31 30 31 31 30 31 30 31 31 28 31 30 31
and correct output is "YES"
Doesn't this show two consecutive leap years? year 1: 31 28 31 30 31 30 31 31 30 31 30 31, next year: 31 28 31 30 31 ... this should not be possible right?
A leap year has 29 days.
Oh god. I can't believe I made this mistake D: So stupid of me.
Thanks though!
Look at all the people who failed problem B. They all did same mistake as you. It's because of the problem statement, January, 28 or 29 days in February (depending on whether the year is leap or not) , which gives an idea that correspondly leap has 28 days and not leap has 29 days.
I solved C by just making two set and giving element to the smaller sum set in a reverse sorted order.I don't know why this works though. Can anyone help me with proving this method's correctness or tell where it could fail?
I am trying the same approach and in pretest 5 59998 its failing as i am putting 48950 twice. I am not sure why only that case failing :|
EDIT: a lot of other cases are also failing. have to do something else,
Try to do it in reverse order, so construct your sets starting with n, then n-1, and so on. This will give you a correct solution.
A set of 4 numbers can always be divided into two sets so that their differences is 0. Take n, n-1, n-2, n-3. Set1 contains n, n-3 and Set2 contains n-1, n-2. When dividing a consecutive sequence, you can always start from the last, take a group of 4 consecutive integers, and start dividing like earlier.
If you can't take a group of 4 consecutive integers, the sequences left might be: i) 1, which can be assigned to any set. ii) 1, 2 : where 1 can be assigned to one set and 2 can be assigned the other set. iii) 1, 2, 3: where 1 and 2 has to be assigned to one set and 3 has to be assigned to the other set.
Your algorithm automatically takes care of the first step. When it assigns n to one set, and n-1 to another, then n-2 becomes assigned to the set containing n-1 and n-3 becomes assigned to the set containing n.
Your algorithm also automatically takes care of the 2nd step. A quick thinking will reveal why.
Hope you understood! :)
good explanation .
Can someone please explain solution to problem E. I don't understand the editorial.
Understood from others solutions :)
A much easier solution for C : My solution link... 1. Just take the sum of the numbers= N*(N+1)/2.
3.If sum is odd, then logically one group will have one more sum than other group(g2). Let G2 sum be x. Keep giving the largest numbers possible to form x
I have also done with similar approach.
I wonder why the writer didn't explain in this way. Are there any cases that this approach doesn't work properly?
All of them worked. This solution seems more intuitive to me compared to one in the editorial.
Can someone explain D? Why we are adding those numbers etc..
难得有一次cf这么适合Chinese。。。
结果差点忘记比赛..晚了几十分钟
Easier way to solve problem C . The sum of the first N numbers is N * ( N + 1 ) / 2, let's call it tot.
If you have a number X less than or equal tot, it is possible to represent it as a sum of first N numbers. ( Iterate from N to 1, and subtract when possible), call that function represent(X). This is very well known.
Now .. if tot is even, we can obtain a difference of zero which we obtain by represent(tot/2). If tot is odd, we can obtain a difference of one which we obtain by represent(tot/2).
In even case, we get the best possible answer, in the odd case it's easy to see that the best we can obtain is a difference of one, and hence the algorithm is optimal.
Another way to solve F is keeping a treap for each character. However, it is overkill in my opinion. But if you have template ready to be copied and pasted, then it should be fastest solution.
Why crash?
http://codeforces.me/contest/899/submission/33344155
You are using this loop:
As soon as you do
ya.erase(re), the iteratorreis invalidated (refer to the first line in heading Iterator validity), so you get unexpected behavior, i.e., you shouldn't usereanymore.Thank you so much!
In problem D we can use a binary search for counting the number of pairs with a fixed amount on a interval: 33359972
Hey anyone got the solution of E by simulating the process using stacks, as i am getting stuck somewhere in this implementation.
Hi guys! Can anybody help me with problem F ?! I tried to solve it using a Multimap and a Fenwick Tree for building the initial positions but I'm getting "Wrong answer" on test 7 :(( Maybe I omit something. Thx in advance!
I solved it by checking if some char already deleted. If yes, don't update
I have a doubt in Problem E.
While merging the two nodes, I can see how we are deleting the right and the left element from the second set(called segments), and then inserting the merged set. I don't understand, how can we perform the same operation in the first set(called lens) ?
we know the position of the beginning of the segment and the length of the segment. so we can just use set.find
Got it. Thanks!
Hey guys! Here are some of my thoughts on problem E this round, using priority queue and linked list! Have a glance! Use of Linked List and Priority Queue in CF Round 452, Problem E
can you please explain how the merge section and del function is working? I am a beginner and unable to understand it directly from your code.
Yeah. The del function will be called when I need to remove a node.
For the merge function, when I remove a node, I need to consider whether the node on the left and the one on the right will merge to a longer sequence. For example, after delete [2,2,2,2] in [3,3,3,1,1,2,2,2,2,1,1], the two sequence [1,1] and [1,1] merge together and become a long sequence, that's what the merge function does.
thanks for your reply :)
Can you please repost it ? Blog on current link has been removed.
In 899F, I didnt understand how would change the current l,r to positions in initial string using segment tree?
we can use binary search the prefix sum on the segment tree。
Please elaborate a bit more.
Sure。 We define a sequence a, a_i equals 0 if the ith element of the original sequence has been deleted, otherwise a_i equals 1. If we need to find the current position of the xth element in the original sequence, then it is equivalent to the smallest i that satisfies the sequence sum [i] = x. Because the sum function is incremented, we can use the binary search to find i that satisfies the condition, This i is the current position of the xth element in the original sequence. We can use the segment tree to maintain this sequence a.
Thanks again.
What does it mean for an item to be in the ith position? It means that before it there are i — 1 items before it.
Now assume for each query you have a data structure that tells you for each original index of the string, how many non deleted elements are before it.
Now to find index L, you just need to find index i such that there are l — 1 non deleted items before it.
Can be done by Binary search + fenwick tree or segment tree.
Got it. Thanks.
Hello guys, Happy Coming New Year to everyone! Can somebody help me, why do I keep getting TL7? Thanks in advance. Solution
Problem C
Can be solved greedily:
Start with putting
Non the left pile andN - 1on the right one. Then by placingN - 2on the right andN - 3on the left we gotleft - right == 0and we reduce the problem to the one of the sizeN - 4.At some point we end up with one of four possible problem sizes:
0, 1, 2, 3.In the first case the difference was
0and it's the best we can do.In the second case we get
1which is also the best solution because in than caseN = 4k + 1and thesum = N * (N + 1) / 2 = (4k + 1)(2k)is odd.In the third case we end up with two numbers:
1and2, the best diff of1and2is1again and again it is optimal sinceN = 4k + 2andsum = (2k)(4k + 3)is odd.In the last case we have numbers
1,2, and3, we can place them so diff will be0which is optimal.The code
This tutorial is not attached to the contest (I can see only Announcement link from there).
Problem F can also be done using sqrt decomposition.
Don't you think the editorials should be more elaborate(eg they can include one example).
Can anyone please explain why in problem D we are adding P/2 to the answer when P <= n+1 ?
Because you can take P/2 pairs to form P as sum. Take as example, P = 9 and N+1 something bigger. To form P = 9 as sum of two numbers you can take, 1-8, 2-7, 3-6, 4-5. As you can see if you continue you will take 5-4 which is similar to 4-5. So moving until the middle of P gives you all the pairs and so P/2 occurs.
I've been stuck for ages... anyone know what test #33 was on div2E? http://codeforces.me/contest/899/submission/33345602
My answer is 1 + the correct answer. :(
Another solution for F :
Store the positions of every character in an array of Sets (like the tutorial)...
Then after each query we can find the original position which has the Kth order after the previous updates by storing original positions in a Binary Search Tree, such as Treap which I used and delete them from the tree while applying the query. Therefore you can get the range query according to the original positions then you can remove positions from the corresponding set using lower_bound like the Tutorial..
(Sorry about my bad English)
in C for 5998 the answer should be 0
bcoz if n is even then we can always keep all the numbers whose %4 gives 1 or 0 in the first group, while others in the second group. This always give us an absolute difference of 0.
plzz correct me if I m wrong?
sorry I found out my mistake, but could anyone provide a proof for C
Link to a submission based on my proof:
36503825
Let's consider first when n is even. Suppose that our solution is A = {2, 4, 6, ..., n} and B = {1, 3, 5, .., n - 1}. We see that
, and therefore the difference between A and B is exactly . We can reduce this difference to zero or one by swapping elements between A and B.
. We can reduce this difference to zero or one by swapping elements between A and B.
If we swap two elements x and x - 1 from A and B respectively we see that we have decreased the absolute difference by exactly two and, in general, we will only be able to reduce the difference in even amounts. Given that the difference is we need this amount to be even in order to be able to reduce it to zero or, in other words, n must be a multiple of 4. If it is not, we will only be able to reduce it to 1. After performing
we need this amount to be even in order to be able to reduce it to zero or, in other words, n must be a multiple of 4. If it is not, we will only be able to reduce it to 1. After performing  swaps the difference will reach one of these two values.
swaps the difference will reach one of these two values.
If n is odd we have A = {2, 4, ..., n - 1}, and B = {1, 3, 5, ..., n}
, and these two solutions can be transformed again to vectors that have difference zero or one by swapping x with x + 1 that belong to A and B respectively. The same arguments about being a multiple of 4 hold for the floor of
Жесть я даун
I think Binary Search tag is missing in Problem F.
Problem E is tagged with flows , i wonder how can we solve this using max flow ?