| # | User | Rating |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 164 |
| 1 | maomao90 | 164 |
| 3 | Um_nik | 163 |
| 4 | atcoder_official | 160 |
| 5 | -is-this-fft- | 158 |
| 6 | adamant | 157 |
| 6 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 8 | nor | 154 |
| 10 | djm03178 | 153 |
http://www.spoj.com/problems/BORING2/
The problem asks to compute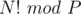 
for prime P
where
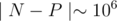
Unfortunately,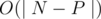 
doesnt pass!
UPD: I have thought about an alternate approach by calculating factorials using their prime factorization (Legendre's formula). But I am not sure if it is fast enough.
Wilson's Theorem looks like a logical first step. The problem reduces to the main difficulty of finding N! mod P for N<= 1e6.
There are many speedups for computing N! mod p apparently (as I just found by Googling). I'm not sure which solution is intended, but it seems that https://en.wikipedia.org/wiki/Montgomery_modular_multiplication might come in useful for a "constant factor" speedup.
http://www.geeksforgeeks.org/compute-n-under-modulo-p/ also looks interesting.
Since you wrote O(|N-P|) you probably know this already, but it's faster to compute N! then take the inverse than multiplying inverses of 1 through N.