Блог пользователя JOF

Interesting problem from Croatian olympiad
Автор JOF, история, 7 лет назад, По-английски

Please help me to solve this problem.

Given a permutation of 1,2...,N numbers. There are 3 types of queries.

  1. perform K times cyclic shift of the segment [l,r] to the right.

  2. perform K times cyclic shift of the segment [l,r] to the left.

  3. Print which number is at position X in current array.

Size of array N (2 ≤ N ≤ 100 000). Number of queries Q (1 ≤ Q ≤ 100 000).

Sample test
  • Проголосовать: нравится
  • +1
  • Проголосовать: не нравится

»
7 лет назад, # |
  Проголосовать: нравится +1 Проголосовать: не нравится

You can use Treap or Sqrt-decomposition. To make cyclic shift to right you should put last K elements to the beggining of the segment. You can do it using split operation.

→ Ответить
»
7 лет назад, # |
← Rev. 2   Проголосовать: нравится -10 Проголосовать: не нравится

Can be done with implicit treap (if you don't know what that is, go look it up).

Then first query (cyclic shifting to right) can be done as follows:

  1. Get the treap corresponding for [L, R] (2 splits). Lets call this treap M.
  2. Split treap M into two treaps ML and MR, such that MR consists of the last K elements.
  3. Merge treaps MR|ML into M (in this "reversed" order)
  4. Insert M back to the general treap (2 merges).

Obviously the complexity will be .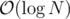

The second operation is equivalent to cyclic shifting to right with R - L + 1 - K.

The last query can be easily done with 2 splits and 2 merges or by simply by traversing the treap.

The overall complexity will be .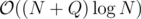

PS: You can do this with sqrt decomposition (as you can easily perform split/merge with sqrt decomposition). That way the complexity for a cyclic shift will be and for the query .

→ Ответить
  • »
    »
    7 лет назад, # ^ |
      Проголосовать: нравится -11 Проголосовать: не нравится

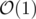    Thank you for your solution. I guessed that there is a solution with data strucutures. If it's not hard for you, please, could you describe your solution with sqrt decomposition?

    → Ответить
»
7 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

My sqrt-decomposition code It's basically maintaining a doubly-linked list in O(sqrtN) time

→ Ответить