JOF's blog

Interesting problem from Croatian olympiad
By JOF, history, 7 years ago, In English

Please help me to solve this problem.

Given a permutation of 1,2...,N numbers. There are 3 types of queries.

  1. perform K times cyclic shift of the segment [l,r] to the right.

  2. perform K times cyclic shift of the segment [l,r] to the left.

  3. Print which number is at position X in current array.

Size of array N (2 ≤ N ≤ 100 000). Number of queries Q (1 ≤ Q ≤ 100 000).

Sample test
  • Vote: I like it
  • +1
  • Vote: I do not like it

»
7 years ago, # |
  Vote: I like it +1 Vote: I do not like it

You can use Treap or Sqrt-decomposition. To make cyclic shift to right you should put last K elements to the beggining of the segment. You can do it using split operation.

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it -10 Vote: I do not like it

Can be done with implicit treap (if you don't know what that is, go look it up).

Then first query (cyclic shifting to right) can be done as follows:

  1. Get the treap corresponding for [L, R] (2 splits). Lets call this treap M.
  2. Split treap M into two treaps ML and MR, such that MR consists of the last K elements.
  3. Merge treaps MR|ML into M (in this "reversed" order)
  4. Insert M back to the general treap (2 merges).

Obviously the complexity will be .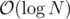

The second operation is equivalent to cyclic shifting to right with R - L + 1 - K.

The last query can be easily done with 2 splits and 2 merges or by simply by traversing the treap.

The overall complexity will be .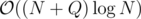

PS: You can do this with sqrt decomposition (as you can easily perform split/merge with sqrt decomposition). That way the complexity for a cyclic shift will be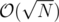 and for the query .

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it -11 Vote: I do not like it

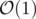    Thank you for your solution. I guessed that there is a solution with data strucutures. If it's not hard for you, please, could you describe your solution with sqrt decomposition?

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

My sqrt-decomposition code It's basically maintaining a doubly-linked list in O(sqrtN) time

→ Reply