Hello Codeforces. I'm trying to solve this geometry problem, but seems I stuck :\ Please help me. Here is the statement:
Given N squares with integer coordinates on plane such that sides of each square is parallel to x/y axis. None of the squares are intersecting. Find how many squares we can see from (0, 0) coordinate. We can see square from O point when there are two different A and B points such that triangle OAB has no any intersection/touch point with other squares. 1 ≤ N ≤ 1000, squares are given to input with its left bottom side coordinates X, Y and its length of side L. (1 ≤ X, Y, L ≤ 10000).
Here is the original statement but only in Russian: http://informatika.edu.az/tasks.php?action=detail&id=150〈=ru
I draw picture of first sample for convenience, input is:
3
2 6 3
1 4 1
3 4 1
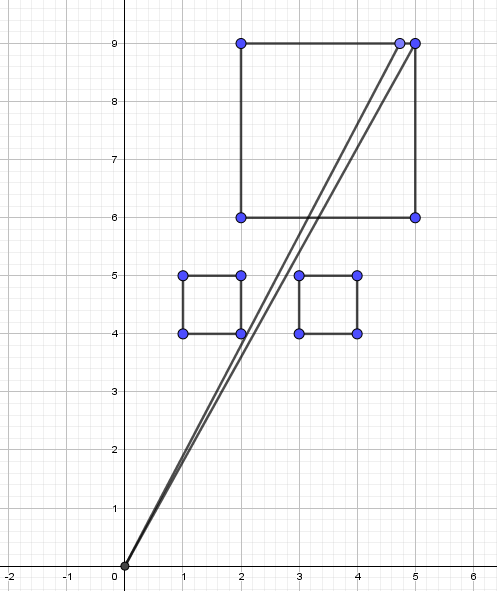
Obviously, we can see two little squares and drawn lines have no intersection points with these little squares so we can also see big square, therefore answer is 3.
Thanks in advance.











Here's an idea:
For each square we will only maintain it's bottom-right and upper-left corners. To make it easier, we will refer to the bottom-right one as the square's right, and the upper-left as the square's left.
Now, the idea is that we sort the squares by the way we can see them from (0, 0). by that I mean, if we look at some direction and we see a square A, that blocks our vision from square B at this angle, then A will be before B in this sorting.
A way to sort could be to look at each square's left point, and specifically at its coordinate sum (if a square's left is (5, 2), the coordinate sum is 7). Let's call this coordinate sum the square's value. Sort the squares by increasing value. This takes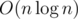 .
.
Anyway, after the sorting, we iterate through the squares and maintain a set of ranges. every range will be denoted by 2 points, and specifically, their slope (to prevent usage of doubles we should use multiplication in the comparator of the set, but I'll refer to it as slope right now).
for each square we're on, we take the set's lower_bound on the slope of the square's left, to find if a square blocks our vision from the current square (and if so, which square). We do the same idea for the current square's right to find if a square blocks our vision there (and if so, which square). If we find that the result of the 2 operations we did on the set is the same square, it means that we cannot see the square we're currently checking. otherwise we can add 1 to the solution.
Right after that, we add the current square to the set (as a range, with its left and right).
All this process is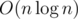 , so the total time is
, so the total time is 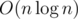 .
.
Correct me if I'm wrong somewhere.