→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
17:47:11
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
17:47:11
Зарегистрироваться »
*есть доп. регистрация
→ Трансляции
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.11.2024 23:47:51 (l2).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











Instead of sorting and finding the biggest two, isn't it faster to just find the biggest two directly?
Correct me if I'm wrong..
maxCapacity[2];
maxCapacity[0]=maxCapacity[1]=INT_MIN
if(capacity>=maxCapacity[0]){
maxCapacity[1]=maxCapacity[0]
maxCapacity[0]=capacity
}
else if(maxCapacity[1]<capacity)
maxCapacity[1]=capacity
this should work right?
Yes that works but it's just easier to code if you sort it.
you wrote solution of C/Div2 and A/Div1 separately !
Thanks it's edited now
could you explain to me Div2-D problem Input 5 1 3 4 5 2 Participant's output 3 4 5 2 1
why WA?
Consider the index subset [1,4] The sum for the given array is 3+2=5 The sum for your array is 4+1=5
Auto comment: topic has been updated by Mahdi_Jfri (previous revision, new revision, compare).
if we follow editorial then answer for 6,10,15 is 5 but the answer is actually 4, where am i understanding wrong, can someone plz explain.(div2 C)
Run second loop(nested one) from i. Not i+1.
still not clear
If you can find the minimum length where gcd is 1 you can make a 1 in len-1 move. As now you find a 1 in the array you can make whole array 1 in n-1 move..total move n-1+len-1
thanks, understood.
This contest was organized well.. well done!
A Div1 can be solved with dp in O(nsqrt(max(ai) + n^2 * log^3(n)) however its almost impossible to do this much operations so my solution is pretty fast 32408288
we could solve in n^2*log(n) by tutorial method
We can solve this in nlog^2(n) with sparse table + binary search or segment tree.
Thank You to all the authors and to the CF team. Great contest! I enjoyed it. :D
someone plz explain div2 C in detail.. with possibly proof..
Which part do you not understand? When cnt1>0 (as given in the editorial) or in the other case?
other case i.e how we get can make the elements 1 in R-L+1+n-1 turns and can you plz explain with example like in case when we have 3 elements i.e. 6 10 15
(Considering that none of the elements are one in the given array)
As soon as we are able to make any of the array elements to 1 the answer will be the steps till now + n-1 as now we can make all of the elements to 1.
So if we have a case in which there are 2 consecutive elements such that their gcd is 1 then the answer will be n (one move for obtaining 1 and n-1 moves for the rest).
If we have no such pairs then we look for triplets. In this case the answer will be 2+n-1=n+1.
Just extend this and you'll get what the author is trying to explain.
For your case gcd(6,10)=2 and gcd(10,15)=5 but gcd(6,10,15)=1 so answer is n+1=4
Hope this helps :)
Hello, I understand what the algorithm is and why it works, but I don't understand how the editorial writer goes about checking the pairs and triples. They basically say to evaluate gcd(L, R) and keep increasing R? How does that work, doesn't that mean you miss pairs at the end? I am probably misunderstanding something.
What the editorial says is that we can fix a L (we do this n times) and by iterating through all the values of R(takes n steps so complexity=n*n) we can find the "smallest subarray" with GCD=1. (Which is what we need to do).
Let's call F(L, R) the gcd of the subarray between L and R, ok?
What is happening is that we can calculate F(L, R) recursively:
F(L, R) = V[L], if L == R or GCD(F(L, R-1), V[R]), if L != R
Now, look at this: --> if F(L, R) = 1, then for every R' >= R, F(L, R') = 1
About the problem: the smartest thing to do is get a 1, as fast as possible, so that we can "carry" this 1 for all the other positions. So, if F(L, R) = 1, we can get a 1, by doing V[L+1] = gcd(V[L], V[L+1]), then V[L+2] = gcd(V[L+1], V[L+2]) and so on, until reaching V[R] = 1.
Now we want to find the minimum R-L+1 that F(L, R) = 1 to get the answer, and we can brute force at each possible L to find the first R that solves the problem.
Can someone provide solution for Div1/E using generation functions?
Sure. Say that we end in the state (a1 - b1, a2 - b2, ..., an - bn), obviously with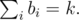 Then one can check by induction that regardless of the path taken to get there, we will have
Then one can check by induction that regardless of the path taken to get there, we will have 
Therefore, it suffices to compute
Note that in the last sum, this is precisely the [xk] coefficient of the following generating function:
Now multiply out the last polynomial: say that
This is O(n2) time to do, or with FFT (unnecessary here). Then we can compute that the [xk] coefficient of the last expression (by expanding out enx) is
with FFT (unnecessary here). Then we can compute that the [xk] coefficient of the last expression (by expanding out enx) is
Putting this all together gives that the answer is
Very beautiful solution!
damn, this is beautiful
It's solution without generating function is really nice!
:D
How do you solve it without generating functions? I think the most beautiful part is that the sum is the same regardless of the path. I can't believe I didn't see it. It's a really nice problem anyway.
I've solved it without generating functions, just with some combinatorics. Everytime, when we increase res, we add to it multiply of things like this: (ai - 1 - 1 - 1... - 1 - 1). So in every bracket we have to decide what will we take: ai or - 1. Let's assume that we will take - 1 p times. We will have to take multiply of some n - 1 - p numbers from input, here goes dp. So we have p+1 empty places, and we should put - 1 in them (p + 1, cause we must calculate result while decreasing some element). Number of ways to choose them is k * (k - 1) * (k - 2)...(k - p). But we have to decide from which - 1 will we be decreasing while increasing res this time. It appears, that we can do it in exactly one way, cause we should choose the latest - 1 (cause all other - 1 must be already added to numbers). k - 1 - p other - 1s can go anywhere, so nk - 1 - p.
it is the of essence generating functions.It’s just different way to get the answer.you use Dp,and tutorial use a mathematical method.
Could anyone explain me the solution to div2 D. I can't seem to understand why this always works. For 4 4 1 2 3 wouldn't the output be 4 1 2 3?
It doesn't mean sort and then shift, even though that what it says. It means: for a sorted array we can just cyclic shift. For an un-sorted array, we do the same thing: replace the i-th smallest element with the (i + 1)-th smallest, and replace the largest with the smallest.
I finally understand. Thank you so much.
Can anyone tell me why my (supposedly) nlogn solution for E keeps getting TLE? http://codeforces.me/contest/892/submission/32410117
In the begining of main function you put "ios::sync_with_stdio(false);" without "cin.tie(0); cout.tie(0);".. This may be the reason.
What do those do? Is having cout.flush() at the end enough?
Explicitly, I don't know.
What I know is that those three instructions become useful for fast I/O when they come together :D.
Lol thanks, it worked :D
Haha welcome, Congrats :D
I am unable to understand the solution for 892-B Wrath. Can anybody please explain?
Can someone explain Div 2E / Div 1C solution a bit more detail ?
I can explain my online solution — it would be a good way to verify if it's correct.
An edge is in some MST if and only if it is not the heaviest edge in every cycle. To check that I used Kruskal. I process all the edges with weight X at the same time. If an edge connects 2 vertices which are already in the same component, it is the heaviest in the cycle. Otherwise it will not be the heaviest in every cycle as we constructed everything we could so far, using edges with weight < X and these vertices are still in separate components. It means that every cycle in which that edge can exist would have edges of weight >= X.
The following part has been modified — not fully verified:
In addition to that, not all of these edges with weight X can exist within the same MST but they can exist separately in some MST's. The problem is that they can create a cycle, when we include cheaper edges. In order to detect such edges we can remember the state of each vertex (the id of components of both vertices when we process an edge in Kruskal).
Now I process queries — I check that every edge can exist in some MST. If that's the case, there is one more thing to check: that these edges do not form cycles — I just run another Kruskal on them, using remembered component numbers.
I understand your idea! But could you explain more the way you create graph G'? I mean how you do it? For example, I have some edges: ~~~~~ (1 2 1) (1 3 1) (3 4 1) (2 5 3) (5 6 3) (6 4 3) ~~~~~ Then, all the egdes with weigt 3(2-5,5-6,6-4) must be in graph G' right?
Thanks for that question, after more thinking I found a bug in my solution. I provided a test which fails it above.
In A Div.1/C Div.2 you make a little mistake, i think the result should be "(R - L) + (n - 1)"
In div2c, what if
n<=10^5 and a[i]<=10^6?We can solve using segment tree with binary search in O(nlogn*logn). And also we can solve it in O(nlogn).
actually the original problem was with limitation n < 1e5 and a[i] < 1e9 but we decided to change it. You can see O(nlogn) solution here by omidazadi
A brief explanation please, thanks!.
Thanks for the detailed explanation of Div-1 C. Hope your fingers didn't start cramping after writing all this.
Div1-C says "It is guaranteed that the sum of ki for 1 ≤ i ≤ q does not exceed 5·10^5", but test case #58 seems to violate this rule.
Can someone prove the validity of the solution of the 891C-Envy question?
In DIV1-C "If ans only if", I think it may be "If and only if"?
can someone explain the DIV 2-E in detail as I am not getting the tutorial solution
Can you tell me how to come up with solution for div 2 D? I have read the editorial, understood how it works but don't know how to deal with same problems.
Can someone explain in Div 2 problem B — Wrath how to maintain the min(j — Lj) for i + 1 <= j <= n in O(n) ?
You can do that without additional memory. Iterate line from the end and maintain killer index. Set index to current person if current person's claw extends further than current killer's claw. See this submission for implementation example.
Thanks now I got it.
I still not clear about the problem DIV2 E/ DIV1 C.
Why is "_It can be proven that there's a MST containing these edges if ans only if there are MSTs that contain edges with same weight_" and "_if we remove all edges with weight greater than or equal to X, and consider each connected component of this graph as a vertex, the edges given in query with weight X should form a cycle in this new graph_."
Can someone explain a little bit more detail about this?
I can give you my understanding of that, consider edges with weight X in query, we remove all edges with weight greater than or equal to X in graph. In this new graph, we consider if the edges with weight X in query is "neccessary". If the edge connect two nodes which have already been connected, we called this edge "unnecessary", if there is an "unnecessary" edge in query, the answer will be NO.
Oh now I got it! For the edges with weight i in each query we need to check all of them to see if they form a cycle or not. Of course we need to process weight i in non-decreasing order and eliminate all remaining edges that have weight >= i.
Thank you very much!
can u please explain me a bit more! why we are considering the edges which have weight = 'i' ? why we are not checking the edges with weight < i?
Can anyone explain the solution idea of problem 891C — Envy (Div 2 — E / Div 1 — C) ? I have read the editorial but I can't understand anything about the idea. Please help.
Soooo Div1 B could be solved in O(N * log N). How come N was only 22? This really bamboozled me during the contest :D
Reason is here.
Ah, that kinda makes sense. Interesting to see problems in which checking the correctness of an answer is (exponentially) harder than generating a correct answer.
can anyone please explain me DIV2-D a bit more ? I didn't understand it completely !
In the editorial of PRIDE, should n't the answer be (R - L) + (n - 1) instead of (R - L + 1) + (n - 1) as in (R-L) steps. We can get a 1 in the segment by taking gcd of consecutive numbers.
For 891B — Gluttony What if the input array is already in the form of sorted then shifted by one? Wouldn't it be the same as the submitted array, leading to WA?
Agree with you (unless we wrongly understood what was mentioned in the editorial). In fact I tried to implement it the way described in the editorial, but it does not pass the tests.
When you sort the input array 'a' you'll have to keep track of indices where the elements were originally present in 'a'. For this, you can use a vector of pairs having first and second 'a[i]' and 'i'.
We shift so that all the indices (except one) the newly formed array(after sorting and shifting) will have elements greater than 'a'.
The sorted vector 'v' from first para will help to arrange in this manner. the 'ith' element of v (i.e. v[i].first )would be placed at the position where the i-1th element was present (i.e. v[i-1].second).
Please explain Div. 1 C , unable to comprehend from editorial.
http://codeforces.me/blog/entry/56000#comment-397225
Hope this helps.
could anyone explain to me Div2-D and why Input 5 1 3 4 5 2 Participant's output 3 4 5 2 1 is WA
The same problem was here: there are two sets of indexes which their corresponding elements have equal sums. S1 = {2,5}, S2 = {3,5}. But I still haven't the accepted solution.
Sorry for my bad English. I solved the problem 891C - Envy offline, but i think that maybe this cant be solved online, whit a persistent union find. My idea is run Kruskal Algorithm and save for the last edge of every weight the estate(persistent) of the union find and for each query sort it by weight and for each "group" of the same weight in the query try to use when the union find only contains edges of weight lower that the actual weight(simulate the Kruskal Algorithm), if every edge is used in the union find then the answer is "YES" I try to implement this with persistent array(segment tree on my case) and get MLE on test 16: 35112572 and try to use garbage collector and get TLE again, someone know a good implementation of persistent union find?
I just ACed with my own persistent dsu implementation and a bunch of optimizations.
https://codeforces.me/contest/891/submission/109523741
Enjoy :)
This solution is fully online :D
can anyone help? 1 10000000 why answer is not -1 in div2 D. Gluttony
Size of the set should be < n
thanks bro got it!
In the solution to 891C-Envy, it says the following:
"So for each query we need to check if the edges with weight X have a MST"
How exactly is X defined? I don't quite understand the solution. Any help / pointers will be appreciated.
I don't understand DIV1 B solution, what if that sorted and shifted array is in the input then it's wrong. Can anyone explain it to me a bit?
If you're given an array of unique elements like $$$[1,2,3,4]$$$ then it's easy to see that a shifted array like $$$[2,3,4,1]$$$ would work. So if you're given an unordered array, do the same value shifting as if it were sorted, except the indices are not necessarily sorted.
why should we make the test data(#58) of Div.1 C so big? I got TLE using cin and ios::sync_with_stdio(false) but AC with scanf. :(