Блог пользователя bazsi700

std::lower_bound vs std::set::lower_bound
Автор bazsi700, история, 7 лет назад, По-английски

I have just discovered, that std::set::lower_bound for larger sets is much-much faster than std::lower_bound.

Can anyone give explanation why does this happen?

Also, use std::set::lower_bound instead of std::lower_bound, I struggled on a problem for like 2 hours because of getting TLE for this.

  • Проголосовать: нравится
  • +4
  • Проголосовать: не нравится

»
7 лет назад, # |
← Rev. 2   Проголосовать: нравится -8 Проголосовать: не нравится

std::lower_bound это бинпоиск по элементу и в данном случае он работает за N * log2, в то время как std::set::lower_bound это проходу по дереву который суммарно ищет за log

→ Ответить
  • »
    »
    7 лет назад, # ^ |
      Проголосовать: нравится +5 Проголосовать: не нравится

    У std::set нет итератора произвольного доступа

    → Ответить
»
7 лет назад, # |
  Проголосовать: нравится +24 Проголосовать: не нравится

http://www.cplusplus.com/reference/algorithm/lower_bound/:

On non-random-access iterators, the iterator advances produce themselves an additional linear complexity in N on average.

http://www.cplusplus.com/reference/set/set/:

iterator — a bidirectional iterator to const value_type

→ Ответить
»
7 лет назад, # |
  Проголосовать: нравится -15 Проголосовать: не нравится

As far as i know std::lower_bound works with complexity O(log n) * O(access_of_element), it is O(log n) for vectors, arrays, but for sets it is something like O(n * log^2 n) (because you can get element in set in O(n log n)). std::set::lower_bound is function specified for using in sets, it has complexity O(log n).

→ Ответить
  • »
    »
    7 лет назад, # ^ |
    ← Rev. 2   Проголосовать: нравится 0 Проголосовать: не нравится

    Actually,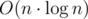 std::lower_bound on a set is (not much better anyway). See this StackOverflow question and, especially, WaltK's comment.

    → Ответить
    • »
      »
      »
      7 лет назад, # ^ |
        Проголосовать: нравится 0 Проголосовать: не нравится

      Yes, i just thought that we need about O(log n) operations to go to the next element in rb-tree every time, but it is O(n) in total, so final complexity is O(n * log n).

      → Ответить
    • »
      »
      »
      7 лет назад, # ^ |
        Проголосовать: нравится +46 Проголосовать: не нравится

      I'm pretty sure it's implemented in O(n)

      → Ответить
      • »
        »
        »
        »
        7 лет назад, # ^ |
        ← Rev. 2   Проголосовать: нравится 0 Проголосовать: не нравится

        I'm not so sure.

        Performs approximately log2(N)+1 element comparisons (where N is this distance).

        It is a binary search, after all, and generally cannot be replaced with a linear one, because the comparison function might have insanely huge complexity.

        In my STL implementation:

        template<typename _ForwardIterator, typename _Tp, typename _Compare>
  _ForwardIterator
  __lower_bound(_ForwardIterator __first, _ForwardIterator __last,
        const _Tp& __val, _Compare __comp)
  {
    typedef typename iterator_traits<_ForwardIterator>::difference_type
  _DistanceType;

    _DistanceType __len = std::distance(__first, __last);

    while (__len > 0)
  {
    _DistanceType __half = __len >> 1;
    _ForwardIterator __middle = __first;
    std::advance(__middle, __half);
    if (__comp(__middle, __val))
      {
        __first = __middle;
        ++__first;
        __len = __len - __half - 1;
      }
    else
      __len = __half;
  }
    return __first;
  }
        → Ответить