Div. 2 A — Драконы
Заметим, что если Кирито сражается с драконом, сила которого меньше силы Кирито, то Кирито ничего не теряет — наоборот, его сила увеличивается на целое неотрицательное число. Поэтому будем всё время выбирать какого-либо дракона с меньшей силой, чем у Кирито в данный момент, и сражаться с ним. Так будем продолжать до тех пор, пока не победим всех драконов (тогда ответ — «YES»), или пока не останутся только драконы, которых Кирито не может победить (тогда ответ — «NO»). Дракона на каждом шаге можно искать по-разному — как проходиться по всем драконам, так и сначала отсортировать драконов по возрастанию силы.
Сложность решения — O(n2) или  . Пример решения: http://pastie.org/4897164 (сохранённая копия)
. Пример решения: http://pastie.org/4897164 (сохранённая копия)
Div. 2 B — Т-простые числа
Можно показать, что Т-простыми являются только квадраты простых чисел, и их не так и много — столько, сколько есть простых чисел, не больших 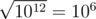 . Вычислим все эти числа (например, с помощью решета Эратосфена) и запишем в массив или
. Вычислим все эти числа (например, с помощью решета Эратосфена) и запишем в массив или std::set, тогда на каждый запрос можно отвечать, просто проверяя (двоичным поиском для версии с массивом), есть ли данное число среди заранее вычисленных.
Сложность решения линейная от n — 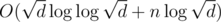 или
или 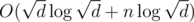 , где d = 1012 (можно вывести и более точную оценку). Пример решения: http://pastie.org/4897166 (сохранённая копия)
, где d = 1012 (можно вывести и более точную оценку). Пример решения: http://pastie.org/4897166 (сохранённая копия)
Div. 1 A — Сдвиги
Посчитаем для каждого столбика, каким минимальным количеством операций в этом столбике можно получить все единицы. Для этого для каждой строки сделаем два прохода, один слева, а другой справа, поддерживая номер ближайшей с соответствующей стороны единицы. Таким образом для всех позиций мы узнаем расстояние до ближайшей единицы. Тогда для одного столбика ответом является сумма этих значений. В свою очередь, ответом на задачу является наименьшая из этих сумм.
Сложность решения — O(nm). Пример решения: http://pastie.org/4897169 (сохранённая копия)
Div. 1 B — Планеты
Можно заметить, что если мы посещаем конкретную планету, то выгоднее всего как можно раньше прибыть на неё, а потом подождать ближайшего свободного момента, и тогда отправиться дальше. Поэтому задачу можно решать с помощью алгоритма Дейкстры, немного поменяв определение кратчайшего пути. Когда мы рассматриваем очередную планету (то есть, мы уже знаем минимальное расстояние до неё), надо пройтись по соответственному списку моментов времени и найти первый момент, когда из этой планеты можно отправляться снова — этот момент и будет расстоянием, которое мы будем добавлять к путям, исходящим из этой планеты. Понятно, что по каждому списку мы пройдёмся не более одного раза. Ещё надо обратить внимание на случаи, когда путешественник прибывает на планету 1 в момент времени 0 (тогда Джек должен ждать), и когда путешественник прибывает на планету n одновременно с Джеком (тогда Джек не должен ждать).
Сложность решения — 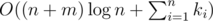 . Пример решения: http://pastie.org/4897171 (сохранённая копия)
. Пример решения: http://pastie.org/4897171 (сохранённая копия)
Div. 1 C — Треугольники
Назовём рёбра Боба антирёбрами. Для каждой пары рёбер полного графа, которые проходят через одну вершину, присвоим вес: каждой паре рёбер значение +2, каждой паре ребро и антиребро — значение −1, и каждой паре антирёбер +2. Посчитаем сумму всех значений. Можно заметить, что каждый треугольник даёт в сумме вес +6, а все остальные комбинации из трёх вершин дают вес 0. Саму сумму считаем, для каждой вершины считая вес каждой пары рёбер, которые проходят через эту вершину. Если степень вершины d, то к сумме нужно прибавить 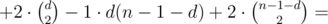 d(d - 1) - d(n - d - 1) + (n - d - 1)(n - d - 2). В конце остаётся разделить сумму на 6, и получаем ответ.
d(d - 1) - d(n - d - 1) + (n - d - 1)(n - d - 2). В конце остаётся разделить сумму на 6, и получаем ответ.
Сложность решения — O(m + n). Пример решения: http://pastie.org/4897512 (сохранённая копия)
Div. 1 D — Башни
Посчитаем динамику d[i][k] — минимальная высота последней башни, которую мы можем получить, соединив первые слева i башен в не менее чем k башен. Допустим, посчитали динамику для первых i башен. Переберём отрезки башен [i + 1;j], пусть сумма высот на этом отрезке s. Найдём наибольшее k такое, что d[i][k] не больше s. Тогда обновим ответ для d[j][k+1]. Заметим, что при увеличении k увеличиваются и значения d[i][k]. Поэтому сами отрезки можно перебирать по уменьшению j, а подходящее k находить указателем по порядку.
Когда приходим на позицию j, какие-то значения d[j][k] обновлены, а какие-то — нет. Используя то же наблюдение, что при возрастании k возрастает и d[j][k], пройдём по этим значениям в порядке уменьшения k, и будем обновлять минимум для d[j][k]. Это делаем в начале итерации динамики.
В конце найдём максимальный k, для которого существует ответ среди значений d[n][k]. Ответом на задачу является n - k.
Сложность решения — O(n2). Пример решения: http://pastie.org/4897515 (сохранённая копия)
Div. 1 E — Дары
Сперва установим пару фактов, которые будем использовать в решении. Узнаем, с какой вероятностью мы можем получить одно множество из даров, среди которых i-того названия ровно ai даров. Всего таких множеств 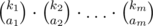 , т.к. множеств элементов i-того названия счётом ai есть ровно
, т.к. множеств элементов i-того названия счётом ai есть ровно 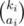 , а два разных названия при выборе ответа независимы. Одно конкретное множество мы тогда можем получить с вероятностью
, а два разных названия при выборе ответа независимы. Одно конкретное множество мы тогда можем получить с вероятностью 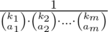 , попросив i-того названия ровно ai штук.
, попросив i-того названия ровно ai штук.
Теперь мы знаем вероятность p получения одного множества элементов A. Заметим, что за константное время мы можем из p узнать вероятность p' получения множества A, к которому добавлен другой элемент x-того названия. Допустим, что в A есть ровно ax даров x-того названия. Используя ранее полученную формулу, можно вывести:
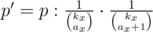
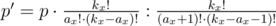
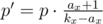
То есть, p' мы можем вычислить за константное время, зная p.
Используя это, решим собственно задачу. Отсортируем все дары в порядке убывания ценностей. Ясно, что названия всех тех даров, ценности которых не равны n-той ценности в этом массиве (обозначим эту ценность как d), нам однозначно надо назвать, чтобы получить n самых ценных даров. Назовём это множество даров базой и посчитаем с помощью формулы вероятность получения базы p. Неопределёнными остаются только те дары, ценность которых равняется d. Потому что, если всего таких даров s, а количество недостающих даров (кроме базы) l, то всего возможно 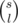 вариантов, как мы можем вместе с названиями даров базы назвать множество остальных l названий, у которого будет шанс получить n самых ценных даров.
вариантов, как мы можем вместе с названиями даров базы назвать множество остальных l названий, у которого будет шанс получить n самых ценных даров.
Теперь у нас есть s «неопределённых» даров с ценностью d, пронумеруем их в каком-то порядке, и назовём их спорными. Будем считать динамику f(x, y) — суммарная вероятность получить n самых ценных даров, если взяли x спорных из первых y спорных. Ясно, что f(0, 0) = p, а f(l, s) — ответ на задачу. Используя ранее найденные коэффициенты, получаем в самой динамике два перехода:
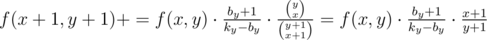 , если к комплекту из x спорных среди первых y спорных добавим y + 1-ое спорное;
, если к комплекту из x спорных среди первых y спорных добавим y + 1-ое спорное;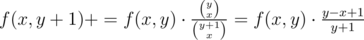 , если, наоборот, не добавляем.
, если, наоборот, не добавляем.
Данную динамику можно посчитать за время O(t2), где t — суммарное количество даров.
Сложность решения — 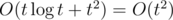 . Пример решения: http://pastie.org/4897519 (сохранённая копия)
. Пример решения: http://pastie.org/4897519 (сохранённая копия)











На мой взгляд, у С (Div. 1) существует решение проще.
Фактически, представим что весь полный граф просто покрашен — каждое ребро или красное, или синее. Нас интересует количество одноцветных треугольников (где все три ребра одного цвета).
Будем искать обратное — количество разноцветных треугольников (где не все три ребра одного цвета). Зафиксируем одну вершину разноцветного треугольника, причём ту, где рёбра из неё разных цветов. Тогда, если из зафиксированной вершины выходит cnt красных рёбер, то ответ для этой вершины = cnt * (N — 1 — cnt) треугольников.
Если мы посчитаем сумму всех этих значений для всех вершин, то получим, что каждый разноцветный треугольник мы посчитали дважды, потому что у каждого разноцветного треугольника ровно 2 вершины, из которых рёбра разных цветов. Делим на 2.
Вот и всё — количество всего треугольников мы знаем: C(N,3), и остаётся отнять от него поделённую на 2 сумму. Тоже O(M + N).
у меня такое же решение
А как все же решать Д? Я вдруг осознал, что моя динамика неверна.
Минут через 15-20 появится в разборе.
Опять же, предлагаю чуть другое решение D (div 1).
Динамика — a[l][r] — минимальное количество ходов, которое нам понадобится, чтобы обработав слева r башен, и все башни от 1 до r уже объединены в неубывающем порядке, при этом последняя башня состоит из объединения башен на отрезке от l до r.
Посмотрим, что может получиться из a[l][r]. Варианта 2:
Просто тупо объединяем следующую башню r+1 с отрезком [l..r]. Очевидно, что ничего хуже получиться не может — неубывающий порядок будет соблюдён. Соответственно, в a[l][r+1] пытаемся запихать a[l][r] + 1.
Иногда выгоднее объединять r+1 вперёд. То есть нам надо найти отрезок [r+1..x] минимальной длины, который не ниже башни [l..r] (её высоту можно найти частичными суммами, но можно и без, об этом ниже). О том как находить — тоже ниже. Не нашли, чтож, печально, значит второго варианта нет вовсе. Нашли, у нас есть новая башня [r+1..x]. Заметьте, что x может равняться r+1, и тогда это получается оригинальная башня, если она уже была выше [l..r]. На её объединение потребуется (x-(r+1)) ходов. Соответственно, в a[r+1][x] пытаемся запихать a[l][r] + (x-(r+1)).
Остался вопрос, как быстро находить такой отрезок. Давайте итерировать по состояниям сначала в порядке возрастания r, а потом в порядке убывания l. Что нам даёт убывание l? Это нам даёт то, что при постепенно увеличивающемся краю l отрезка [l..r], растёт и его высота, соответственно, x будет всё дальше и дальше, и нам надо проитерировать по массиву для поиска х всего N раз — для каждого r. Тут же можно обойтись и без частичных сумм, и опять же постепенно их увеличивать при убыванию l. Опять же — O(N^2).
Кто может сказать какая сложность у этой программы 2281512?
По-моему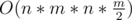 , но правильно ли это? И не долго ли это?
, но правильно ли это? И не долго ли это?
Вот генератор теста, на котором падает решение:
При n = 100, m = 1000 работает 4 секунды, а это не макс ограничения. Сложность решения на нём с точностью до константы будет O(n * n * m * m)
Я не смог в итоге понять правильно ли мое решение, но оно прошло, будем считать такую динамику, dp[i] это минимальная высота, которая получится при суммировании h[k], k принадлежит отрезку [j, i], причем dp[i] >= dp[j — 1], соответственно посчитаем для каждого i, k[i] = i — j + k[j — 1]. Вот 2284974, возможно это weak tests, а может такой подход действительно работает.
Я пострессил решение с правильным на куче рандомных тестов, ошибки не было. Для всяких неправильных решений и жадников стресс довольно быстро находил нам контрпример, так что вполне возможно, что это тоже правильно.
/*
Снова этот магический C++. Видимо, я чего-то не знаю.
Почему на строчке
не возникает ошибки компиляции? Переменная
retвроде бы нигде не объявлена...А, наверно это глобальная переменная, объявленная в одном из заголовочных файлов, так?
*/
Ответ ниже
См. определение макроса
in.А, действительно, я думал там input вызывается. Наверное опасно писать подобным образом.
Div 1 D can be solved in O(n). Very similar problem was at USACO Open 2009: http://tjsct.wikidot.com/usaco-open09-gold problem 3. Unfortunately I can't find any link to the solution. The idea was that making the tower the narrowest is equivalent with making it the tallest, and counting the narrowest tower is somehow easier. I don't remember it very good.
Here is the analysis http://ace.delos.com/TESTDATA/OPEN09.tower.htm
The link doesn't work.
You can find the USACO archive here https://codeforces.me/blog/entry/95032.
Div 1 C's formula is wrong, I think. It's d(d — 1) — d(n — d — 1) + (n — d — 1) * (n — d — 2).
Thanks, fixed.
Не могу сделать задачу С div 2. Кому не сложно, посмотрите пожалуйста в чем ошибка 2298209.
Вот тест:
Правильный ответ — 1.
Видимо, я тупой, но все же. Задача Б. Вот у нас есть Дейкстра. Чтобы алгоритм работал, нужно каждый раз выбирать минимальную по расстоянию из серых вершин. Но вы выбираете минимальную по расстоянию, не учитывая занятые моменты времени, а потом пересчитываете расстояние. После этого оно, казалось бы, может стать не минимальным из серых. Нужный инвариант не выполняется. Почему оно все равно работает?
Пожалуй, там не очень правильно написано (_теперь исправил_). Когда мы рассматриваем очередную вершину (ту из нерассмотренных, расстояние до которой наименьшее), то мы действительно уже нашли минимальное расстояние до неё. То, что мы рассчитываем после — это добавочное расстояние к путям, которые пойдут уже из этой вершины. Получается, что мы пускаем обычного Дейкстру, но длину рёбер знаем не заранее, а узнаём непосредственно перед тем, как будем их рассматривать (при этом «рассматриваемая» длина рёбер может оказаться несимметричной).
да, действительно, спасибо.
in Div1 C we can solve it easier:
let t = number of all possible triangles (n(n-1)(n-2)) / (1*2*3);
we restore degree of vertex like when we scan ai and bi -> x[ai]+=1; x[bi]+=1; where 1<= i <=n
let k = sum of all (di * (n-1-di)); where di = degree of i'th vertex;
then k=k/2; because we count each wasted triangle twice ;)
then answer is t-k :D
in here you must use long long or __int64
in this solution I just removed wasted (made with bob's and alice's edges) triangles from all possible triangle
Can you explain this answer?
I think you didn't understand where I'm getting the k value... lemme explain it :)
I'm counting the wasted triangles.. the wasted triangle forms with connected 3 edges. (1 Bob's edge and 2 Alice's edge.. or otherwise). and it store 2 of vertices which connecting bob's edge with alice's..
I take one vertex, then I'm counting how many wasted triangles with that vertex can form (triangle's vertex connecting both Alice's and Bob's edges). di contains degree of vertex. number of edges going from that vertex (also choosen that is choosen edge by Alice).. I'm multiplying it with Bob's edges starts with that vertex.. that is (n-1-di) and we get the wasted triangle's vertex number's sum...
as we said every wasted triangle stores 2 of vertex with that property (connects bob's edge and Alice's), we have to divide k with 2... we get wasted triangle's number... then remove it from all possible triangle's number. ;-)
/
Once again TLE due to cin and cout without syncing it in div2 B!
Hi, I got struck for Div-2B T-Primes. I am getting TLE for TC-63. Can anyone help?
The same thing happened to me :) I fixed it by: Check if the number is 4. If it is, answer is yes. Otherwise, check if it is divisible by 2. If it is, answer is no. Or else do the classic primality test like this: j = 3; j*j <= sqrt(number); j += 2. (So instead of looping through even numbers repeatedly, we are ignoring them and using odd numbers only because all primes other than 2 are odd).
Accepted code
can someone give me a sample solution for Div.2 B problem — T primes. The sample solution link is not working.
https://codeforces.me/contest/230/submission/81346031 here you go
bro why you have made sieve that contains the no's which are not prime.
Cn we solve it by making sieve that contains prime no's instead and just checking their presence and return true if present?
thanks in advance
no special reason, yes you can do that way as well, just have to revert some flags
okk thanks
87289007
bro why you have made sieve that contains the no's which are not prime.
Cn we solve it by making sieve that contains prime no's instead and just checking their presence and return true if present?
thanks in advance
yes, and you can also do without sieve like this 102172315
I have a really simple 1-dimensional DP solution to problem D of Div1, Towers.
Main idea: for the array $$$a_1 a_2 ... a_N$$$, the minimum number of moves to make it non-decreasing corresponds to the smallest height of the last element of the resulting sequence.
For proving this, we can use induction on the index. Let's say it is true for $$$1...j$$$. Then for $$$j+1$$$, we can show that the number of moves to take last $$$m$$$ elements is less than the number of moves to take the last $$$t$$$ elements, where $$$t>m$$$, which results in the $$$m$$$ case to have a smaller value of the last element. We need the inductive hypothesis to classify $$$m$$$ and $$$t$$$ as valid indices.
Feel free to reply if you have any difficulty.
84694143
I just want to inform that the sample solution links given in the Editorial are not working anymore.
Thanks
Updated the article with links to the Internet Archive.
Thanks!
It Was Very Helpful thank you for this post.
Bro how can i fix that TLE in B .......? i apply every thing (sieve, simple thought) ..what can i do..
can someone tell me what is wrong with my code. it gives error in like 20550th case in 24th test, but i dont understand why...\
include <bits/stdc++.h>
using namespace std; using i64 = long long int; using u64 = unsigned long long int; using u32 = unsigned;
int main() { ios::sync_with_stdio(false); cin.tie(nullptr); int n; cin>>n; while(n--) {i64 a; cin>>a; float k; bool flag = true; if(a==1) flag = false; int j = a;
k = sqrt(a); a = sqrt(a); if(k!=a) flag = false; else { long long int p; p = sqrt(a); if(a%2) for(int i =2;i*i<=k;i++) { if(a%i==0) flag = false; } else flag = false; } if(j == 4) flag = true; if(flag) cout<<"YES"<<endl; else cout<<"NO"<<endl; } return 0;}
nevermind, i chose float insted of double which probably gave error though I still dont know the exact reason