A div2. Куда свернуть?
Посмотрим на векторное произведение 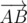 на
на 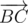 , численно равное
, численно равное 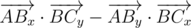 . Знак векторного произведения определяется знаком синуса ориентированного угла между векторами (т.к. векторное произведение также равно
. Знак векторного произведения определяется знаком синуса ориентированного угла между векторами (т.к. векторное произведение также равно 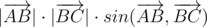 ), а именно этот-то знак нам и нужно узнать.
), а именно этот-то знак нам и нужно узнать.
Если произведение равно нулю, то это в данной задаче означает, что A, B и C лежат на одной прямой, а значит ответ — <>.
Если произведение больше нуля, то ответ — <>.
И, наконец, если оно меньше нуля, то ответ — <>.
Также стоит обратить внимание, что вычисление векторного произведения требуется производить в 64-битном типе, чтобы избежать переполнения.
B div2. Эффективный подход
Пусть число t стоит на позиции indt в первоначальной перестановке. Тогда, очевидно, пробегом слева направо это число будет найдено за indt сравнений, а пробегом справа налево — за n - indt + 1 сравнений. Заведем доп.массив, в i-й ячейке которого будет стоять число j такое, что aj = i. Этот массив позволит обрабатывать каждый запрос за O(1) при помощи указанных выше формул. Доп. массив строится за O(n) пробегом по массиву a. Таким образом, окончательная асимптотика решения O(n + m).
C div2 — A div1. Отсеки летающей тарелки.
Обозначим за Fn ответ на задачу, где n — число инопланетян. Давайте предположим, что мы уже решили задачу для n - 1 инопланетянина, т.е. знаем значение Fn - 1. Попытаемся найти его для n инопланетян. Заметим, что младший по рангу (далее — просто младший) инопланетянин сможет покинуть 3-й отсек только тогда, когда все остальные инопланетяне перейдут в 1-й отсек. Значит, первые Fn - 1 действий нам известны. Далее младший инопланетянин может перейти во второй отсек. Чтобы он попал в 1-й отсек, требуется, чтобы остальные вернулись в первый. Значит, требуется еще Fn - 1 действий. Наконец, после того, как младший инопланетянин перейдет в 1-й отсек требуется еще Fn - 1 действий на возвращение n - 1 инопланетянина в 1-й отсек из 3-го. Таким образом, Fn = Fn - 1 + 1 + Fn - 1 + 1 + Fn - 1. Это уже позволяет найти Fn быстрым возведением матрицы в степень, но мы пойдем чуть дальше. Прибавим по 1 к левой и правой части равенства и после элементарных преобразований получим Fn = 3·(Fn - 1 + 1) - 1. Теперь легко угадать решение рекуррентного соотношения: Fn = 3n - 1.
Осталось научиться быстро вычислять значение Fn. В этом нам поможет бинарное возведение в степень. Асимптотика решения — O(log n).
Осталось упомянуть один "подводный камень": если 3n mod m = 0, необходимо не забыть, что ответ равен m - 1, а не - 1, и разобрать этот случай.
И напоследок маленькая аналогия: перед вами только что была задача о Ханойских башнях с модификацией, заключающейся в том, что переносы дисков разрешены только между двумя парами стержней.
D div2 — B div1. Непослушные кучки камней
Рассмотрим следующую интерпретацию задачи: кучкам камней соответствуют вершины. Операции добавить кучку a к кучке b соответствует операция подвешивания поддерева вершины b к вершине a. Числа, записанные на вершинах, — размеры кучек. Задача — добиться такой конфигурации дерева, чтобы к каждой вершине было подвешено не более k поддеревьев, а сумма произведений чисел, записанных на вершинах, на глубину вершин (где глубина корня равна 0) минимальна. Чтобы добиться минимальности, требуется, во-первых, чтобы вершина с большим числом находилась не ниже, чем вершина с меньшим (иначе их можно просто поменять и получить меньшую сумму), а во-вторых, чтобы у каждой внутренней вершины, кроме, может быть, одной было ровно k потомков (второе условие также доказывается методом от противного). Осталось научиться быстро считать для такой конфигурации саму сумму. Для этого отсортируем массив размеров кучек, а затем будем действовать так: вначале прибавим к ответу сумму размеров кучек с 1-й по k-ю (в 0-индексированном, отсортированном в порядке невозрастания массиве), домноженную на 1; затем сумму размеров следующих k^2 кучек, домноженную на 2; и т.д. до конца массива. Чтобы быстро отвечать на запрос о сумме на отрезке, предподсчитаем суммы на префиксах сразу после того, как отсортируем массив. Теперь при k > 1 мы умеем находить ответ на запрос за O(log n). Если тем же соображениям следовать при k = 1, ответ на запрос будет занимать O(n) операций, а потому решение получит TL, если в большей части запросов k будет равно 1. Поэтому следует заранее посчитать ответ для k = 1 и запомнить его, чтобы отвечать на такие запросы за O(1).
Асимптотика решения — O(n · log n + q · log n).
E div2 — C div1. Юбилей
Сначала докажем ключевое утверждение: НОД(Fn, Fm) = FНОД(n, m).
Начнем издалека: выразим Fn + k через Fn и Fk. Получим следующую формулу: Fn + k = Fk·Fn + 1 + Fk - 1·Fn. Эта формула доказывается по индукции.
Теперь воспользуемся полученной формулой и заметим, что НОД(Fn + k, Fn) = НОД(Fk, Fn).
Осталось заметить в последней формулой аналогию с алгоритмом Евклида и осознать, что мы получили требуемое нам соотношение для НОД двух чисел Фибоначчи.
Итак, мы свели задачу к следующей: найти в заданном множестве подмножество из k (или хотя бы из k) элементов с максимально возможным НОД. А точнее, найти сам НОД такого подмножества.
Пусть ответ равен q. Тогда должно выполняться 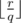 -
- 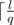 ⌉ + 1 ≥ k (1).
⌉ + 1 ≥ k (1).
Заметим, что для каждого из слагаемых из левой части неравенства существует 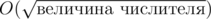 отрезков, на которых его значение постоянно. Причем мы можем найти все эти отрезки и значения за
отрезков, на которых его значение постоянно. Причем мы можем найти все эти отрезки и значения за 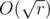 . Точнее, нас интересуют такие q, что в q - 1 значение хотя бы одного из слагаемых меняется (очевидно, увеличивается). Таких значений тоже
. Точнее, нас интересуют такие q, что в q - 1 значение хотя бы одного из слагаемых меняется (очевидно, увеличивается). Таких значений тоже 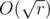 . Осталось перебрать их все и каждое попробовать в роли ответа (т.е., для каждого проверить неравенство (1)), а из подошедших выбрать максимум. Ответ всегда будет, т.к. единица подходит на роль q при любых входных данных.
. Осталось перебрать их все и каждое попробовать в роли ответа (т.е., для каждого проверить неравенство (1)), а из подошедших выбрать максимум. Ответ всегда будет, т.к. единица подходит на роль q при любых входных данных.
Таким образом, мы нашли индекс искомого числа Фибоначчи. Само же число можно вычислить, быстро возведя матрицу в степень.
Асимптотика решения — 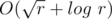 .
.
D div1. Всего лишь таблица.
Научимся получать ответ. Поступим следующим образом: будем находить любую строку или столбец с отрицательной суммой и инвертировать его/ее. Заметим, что сумма всех чисел в таблице после таких операций неизменно будет возрастать. Очевидно, что возрастать бесконечно сумма не может. За один шаг сумма возрастает хотя бы на 2, а максимальное возможное изменение суммы относительно начальной — 200·n·m. Таким образом, всего потребуется не более 100·n·m операций (применения заклинания), каждая из которых выполняется за время O(n) или O(m). Итак, мы научились получать нужную таблицу за ~ 1004 действий.
Осталось восстановить ответ. Легко понять, что в него войдут те строки и столбцы, которые мы инвертировали нечётное число раз.
E div1. Путь благородного рыцаря
Решение 1
Нетрудно догадаться, что замки образуют дерево. Построим на этом дереве heavy-light decomposition. Над каждым путем построим персистентное дерево отрезков на сумму. В вершине дерева отрезков будет храниться 0, если замок на текущий момент не тронут варварами, и 1 в противном случае.
Каждый путь рыцаря можно при помощи нахождения lca разбить на не более чем два подпути, лежащие на пути от одного из концов маршрута к корню. Теперь будем решать задачу для каждого из подпутей отдельно. Будем последовательно обрабатывать пути из heavy-light decomposition и одиночные вершины, принадлежащие подпути. Нас интересует количество вершин на подпути, которые не посещались с года y + 1 по текущий, т.е. (в случае пути из декомпозиции) таких, что разность между значениями в текущей версии персистентного дерева и в версии, соответствующей году y (требуемая версия ищется бинпоиском в списке версий) равна нулю (случай с одиночной вершиной тривиальнее: достаточно просто хранить время посещения вершины). Как только количество подходящих вершин станет не меньше k, нам останется синхронно спуститься по двум версиям дерева, чтобы получить ответ.
Если на первом подпути k-я вершина не найдена, то следует обратить внимание, что поскольку мы идем по дереву всегда снизу вверх, то надо аккуратно пересчитать номер вершины, чтобы узнать, какой она должна быть по счету на втором подпути, считая снизу вверх.
Асимптотика решения: O(m·log2 n) — в каждом запросе первого типа нам может потребоваться обновить какое-нибудь дерево отрезков, на что уйдет O(log n) операций; в каждом запросе второго типа нам встречается O(log n) путей декомпозиции, каждый из которых обрабатывается за O(log n) (вначале бинпоиск по версиям, затем запрос к дереву/спуск по дереву).
Решение 2
Обойдем дерево dfs'ом, записывая в массив номер вершины в моменты входа и выхода (аналогия с правильными скобочными последовательностями). Причем как записи о входе, так и записи о выходе сопоставим 0. На этом массиве построим персистентное дерево отрезков.
Теперь, когда нам будет поступать запрос первого типа, будем сопоставлять позиции первого вхождения вершины в массив + 1, а позиции последнего вхождения — - 1.
Для того чтобы научиться обрабатывать второй запрос, заметим, что для нахождения количества посещенных вершин на произвольном подпути между вершинами a и b такими, что обе вершина a лежит на пути от вершины b до корня, нам требуется найти сумму чисел, сопоставленных позициям между первыми вхождениями вершин в созданном обходом в глубину массиве.
Теперь на каждом из подпутей в отдельности запустим двоичный поиск по ответу — позиции искомого замка. Для проверки ответа воспользуемся приведенным в предыдущем абзаце соображением.
Асимптотика решения: O(m·log2 n) — в каждом запросе первого типа нам может потребоваться обновить дерево отрезков, на что уйдет O(log n) операций; в каждом запросе второго типа O(log n) итераций бинпоиска по ответу, каждая из которых обрабатывается за O(log n).
upd. Исправил маленькую неточность в неравенстве в разборе E div2 — C div1. В левой части добавился +1.











-
И все же мне кажется что стоило С и D поменять местами.
мне кажется, они примерно одного уровня
Могу в разборе местами поменять ;)
А если серьёзно, то да, я с этим согласен и приношу извинения за недоработку. Но сделанного уже не воротишь.
Tower of Hanoi with a slight modification. Sweet.
Problem C Div II looks like(Of course, statement is totally different) the 2nd Exercise problem(Warm Up Section) from the first chapter of Concrete Mathematics (By Knuth, Graham and Patashnik)
In short that problem is: Find the shortest sequence of moves that transfers a tower of n disks from the left peg A to the right peg B, if direct moves between A and B are disallowed. This highlighted condition makes the difference with this problem to the classic Tower of Hanoi problem :-)
Спасибо за код авторского решения!
A получилось чуть ли не слабее В.
В D указанное утверждение "мы нашли таблицу с максимальной суммой" неверно. Действительно, рассмотрим матрицу:
Совершенно очевидно, что сумма любой строки и столбца в ней неотрицательна. Изменим знак второй строки и столбца. Получаем:
Сумма полученной матрицы явно больше.
Исправлено. Спасибо!
Не знаю, что именно исправлено, но неверное утверждение "мы получим таблицу с максимальной суммой" вроде (пока?) никуда не делось.
Возможно, я не очень удачно переформулировал, но теперь в утверждении есть оговорка: "Так что даже если нам будет постоянно не везти", которая подразумевает ситуацию, когда мы не получим валидную таблицу после 1-й, 2-й и т.д. итерации, но рано или поздно, получим таблицу с макс. суммой (т.к. сумма неизменно растёт), которая точно удовлетворяет условию, как доказано выше.
Непонятно, что изменила эта оговорка. В данном контрпримере алгоритм вообще не совершит ни одной итерации, так как отрицательных строк/столбцов нет.
Зачем говорить вообще что-либо о таблице с максимальной суммой? Укажите алгоритм, докажите, что он останавливается и число шагов до остановки.
И в самом деле... Спасибо! Поправил ещё раз.
Excuse me, can anyone help me to type the text under the square root of this Image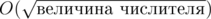
Because I use google translate, and it can't translate the image :P
Thks!
numerator value
Why the number of operations is at most 200*n*m in problem D?
Least possible sum of all elements is (-100) * n * m, greatest possible sum is 100 * n * m. Each turn sum increases (at least by 2), so the number of operations is not greater than 100 * n * m.
nevermind, I found the proof for D confusing. It makes sense now
I used treap as the segment tree's vertices in problem E.It can solve the problem in O(n(logn)^3) and pass the all tests.How stupid I am!
how to deduce the inequality in problem E div 2
Obviously,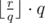 is the maximal number which is divided by q among all numbers between l and r, inclusive. Also,
is the maximal number which is divided by q among all numbers between l and r, inclusive. Also, 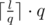 is the maximal number which is divisible by q among all numbers between l and r.
is the maximal number which is divisible by q among all numbers between l and r.
Moreover, each of the numbers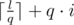 between l and r inclusive are divisible by q. There are exactly
between l and r inclusive are divisible by q. There are exactly 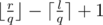 such numbers.
such numbers.
q may be the correct answer if and only if the amount of such numbers is not less than k.
For the problem Div2 E / Div1 C here's a nice proof for the GCD property.
And the expression $$$(1)$$$ can also be written as $$$\left \lfloor \frac{r}{q} \right \rfloor- \left \lfloor \frac{l-1}{q} \right \rfloor \ge k$$$, which says that the multiples of $$$q$$$ within the range $$$[l, r]$$$ must be $$$\ge k$$$.
In div2 A, I find the solution utilizing complex numbers cute :)
In particular let $$$a$$$,$$$b$$$,$$$c$$$ represent the complex numbers having the affixes A,B,C respectively. Defining $$$\text{dir} = \frac{c-b}{b-a}$$$, and $$$\text{unit_dir} = \frac{\text{dir}}{|\text{dir}|}$$$.
We have to
Where $$$j$$$ is the imaginary unit.