KAN's blog

Codeforces Round #424 Editorial
By KAN, 7 years ago, translation, In English
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...

Thanks Arpa for this editorial!

Tutorial is loading...

Thanks Arpa for this editorial!

Tutorial is loading...
  • Vote: I like it
  • +58
  • Vote: I do not like it

Comments Comments (81)
| Write comment?
»
7 years ago, # |
← Rev. 3   Vote: I like it +70 Vote: I do not like it

Me after realizing that I have spent half an hour in the contest on problem E med_1444325338_image_by_totalgymvssonic_da476wb

→ Reply
»
7 years ago, # |
← Rev. 5   Vote: I like it +15 Vote: I do not like it

Also div2 D/div 1 A can be solved using binary search on time in which every man must come to the office. Sort men and keys positions and then on each check: for every man (going from left to right) we should take key lies "as left as possible". If keys are out, then this time (which we were checking) is smaller than answer.

O((n + k) log 1018) if we take answer in range [0;1018]

http://codeforces.me/contest/831/submission/28546197

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +7 Vote: I do not like it

    I just think it is ((k+n)log()) Because, how should you take keyas left as possible? Also because always keys can be contiguos maybe we can do BS on starting key pos?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +1 Vote: I do not like it

      right, I forgot to change it)

      → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +3 Vote: I do not like it

      I thought we can do trinary search on starting key position (when we are moving contiguous set of keys from left to right, time is nonincreasing first, and nondecreasing then), but there is problem when two different starting key positions result in the same time. I don't know how to advance trinary search in that case.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        I remember the same situation in another task, and it was solved (or just partially..) by using bin search from m1 to left and from m2 to right to find first value different from m1/m2, then we can compare them.

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
          ← Rev. 3   Vote: I like it 0 Vote: I do not like it

          But new values can be equal again.

          I can prove that looking for minumum in table of length n which is nonincreasing first and nondecreasing then needs checking at least n-1 elements from that table.

          Let's look at n different input tables which look like this:

          Number 1: 0 1 1 ... 1 1
Number 2: 1 0 1 ... 1 1
Number 3: 1 1 0 ... 1 1
...
Number n-1: 1 1 1 ... 0 1
Number n: 1 1 1 ... 1 0

          So i-th input table have '0' at i-th position and '1' everywhere else.

          All these tables are nonincreasing first and nondecreasing then, so any algorithm solving looking for minumum of such a function have to distinguish these n tables, because answers (place where minimum is) are different for that tables.

          But when algorithm will ask about some position in table of length n and it will find '1', then it just eliminate only one possible input table (that which have '0' in asked position). And for any given algorithm, regardless how it asks about values in table, there exists input table, for which algorithm will ask about '1' n-1 times (opponent can just say that there is '1' in places where algorithm asks). So algorithm for given problem needs to check at least n-1 values to find minumum of table.

          So it is not possible to use trinary search in that task efficiently unless there exists some another observation I cannot see.

          → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +5 Vote: I do not like it

        I solved with binary search for starting key position. http://codeforces.me/contest/830/submission/28644458 You know that the function is strictly decreasing, then strictly increasing. So to determine if you should go high or low you need to check two values and see if they are decreasing or increasing. If they are the same then one is the answer.

        For trinary search you would need to do a similar thing to determine which way to go, check the value right next to the problematic key positions.

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it +1 Vote: I do not like it

          Ok, I didn't see that function is strictly decreasing and strictly increasing.

          → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    what is the proof of "taking continuous key will give us optimal solution" .

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 2   Vote: I like it +1 Vote: I do not like it

      First step: You can show that if some person B is more on the right than person A, person B have to take key which is more on the right than key taken by person A. It is suffiecient to show that you can swap their keys otherwise, not increasing time to both of them go to office (there are few cases to check).

      Second step: You can show that if there is key not taken by anybody between two key taken by some two people, one person can take key in the middle instead of another key and shorten his path.

      And second step imply that there exists optimal solution in which all taken keys are continuous.

      → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I am trying to solve using DP. I defined a recursive function f(i,j). Here i=> ith person and j=> jth key.

    f(i,j) = max(f(i-1,j-1), f(i-1,j), abs(p-j)+abs(j-i)). Minimum of all f(n-1,j) is the answer. What is wrong with this solution. WA test case 8.

    → Reply
    • »
      »
      »
      5 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      sorry my response is 10 months late :p

      I was solving this question today and had a problem similar to yours. You probably forgot to sort all Ai's and Bi's (that was my mistake)

      In my DP, if we don't sort all Ai's and Bi's, the transition between states won't cover all needed cases to find the best possible time. Reason for that is, you could, for a person i, ignore key j and try to get solve(i, j+1) as an answer. But the state (i, j+1) wouldn't consider the previously ignored key j as an option for all persons with index greater than i, and we have no guarantee that it wouldn't be a "good choice" for other person with index greater than i

      By sorting both arrays A and B we guarantee that if person i ignores key j in (i, j) state, it would not make sense for another person with index greater than i consider that ignored key j as an option, because it would increase the answer. So we don't need to care about keys lesser j in state (i, j) anymore, and now our DP covers all needed cases to find best possible time

      → Reply
»
7 years ago, # |
  Vote: I like it +28 Vote: I do not like it

When is the full tutorial for div1 C & D coming out?

→ Reply
»
7 years ago, # |
  Vote: I like it +5 Vote: I do not like it

why the solution to div2 E is so strange? confuzed...

→ Reply
»
7 years ago, # |
  Vote: I like it +12 Vote: I do not like it

how do div1C&&div2F

→ Reply
»
7 years ago, # |
  Vote: I like it +1 Vote: I do not like it

Can anyone explain the solution for div2 E/div1 B ...

KAN Can you translate it to english please !??!

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Use fenwick tree to calculate how many items are left in each prefix. You simulate the algorithm in the problem statement using this.

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +13 Vote: I do not like it

    This picture might help you: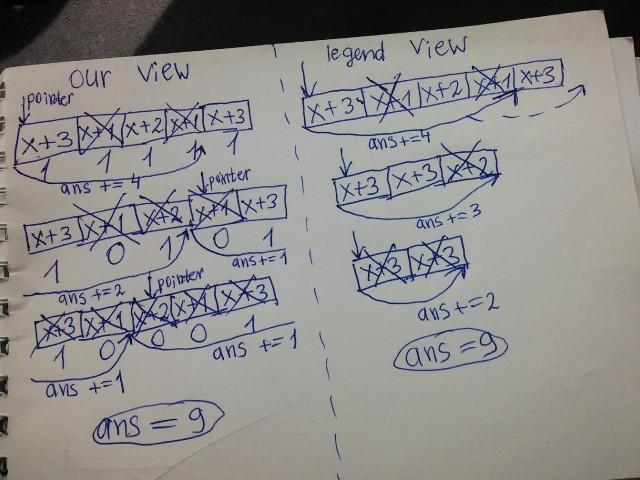

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    Think of elements being removed in rounds.If an element is removed at ith round then it has been looked up exactly i times.We can maintain total elements remaining to remove and add this to the answer at the beginning of the round.It can be done without fenwick trees.Code

    → Reply
»
7 years ago, # |
  Vote: I like it +10 Vote: I do not like it

There are some interesting ways to solve div1 A&B...

For A, binary search an answer K, then link ith person to jth key such that |a_i-b_j|+|P-b_j| \le K, then we can use a maxflow algorithm to check if the answer K is accepted. Then we find out that a person will fit a segment of keys, so we can use segment tree to reduce the number of edges.

For B, just use splay tree to simulate the operations......

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +10 Vote: I do not like it

About div.1 D, I don't really understand the definition of dp[k][c] in the hint. If it means the number of sets which include c non-intersecting paths in k-house, I think the c will be (1<<k)-1 when all paths are single points, that seems ridiculous to me. Can anyone offer to explain it? Thanks.

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it +33 Vote: I do not like it

    Let's consider the dp array, dp[i][j] denotes the number of ways to get j non-intersecting paths in an annoying graph with height i as the promblem shows in the description, it seems that j can be as large as 1<<i , but never mind. Let's see what are the transitions first.

    Now assume we've got all the dp[i-1][x], how can we make it to dp[i][x]? First enum how many paths we have in the left and right child, let's call them l and r. There are 5 types of transitions.

    num = dp[i-1][l]*dp[i-1][r]

    1. Take the root, and make itself a new path ----> dp[i][l+r+1] += num
    2. Don't take the root ----> dp[i][l+r] += num
    3. Take the root, and connect it to a path in the left child ----> dp[i][l+r] += num*l*2
    4. Take the root, and connect it to a path in the right child ----> dp[i][l+r] += num*r*2
    5. Take the root, and it combines two paths ----> dp[i][l+r-1] += num*C(l+r,2)*2

    Now the interesting thing is, every time we go from i to i+1, we can only decrease the number of paths by 1, which means that j>k in the dp[i][j] is totally useless, it won't affect the final answer dp[k][1], so the complexity will be O(k^3) which is enough to pass the test.

    Wish my poor English hadn't make it too hard to understand :D.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Thank you for your quite clear tutorial, I bet I'll understand it soon, after finishing my running contest. Never mind English, I'm from JS, too. 233

      → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      In fact, your English is perfect so I can understand easily. Thank you for your clear answer.

      hint: I'm from JS, too, it's nightmare to recall the exams of English when I was in high school. It seems that you are in high school? Hope you good luck!

      → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone explain the idea behind Cards Sorting ?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    traslated text (still no idea what this means):

    Firstly, we note that the operation "put under the bottom of the deck" is tantamount to "starting from the beginning when the deck ends," without shifting the cards anywhere.

    Next, we will process all the cards with the same numbers at a time, obviously, Vasily will postpone them one by one. Suppose, at the moment when he laid out all the cards smaller than x, he was in some position p in the deck. Then two cases are possible.

    If all the cards equal to x are later than the p position, then he scans all the cards until the last card x, and puts all x equal; Otherwise, if there is a card equal to x before p, it will first scan all the cards to the end of the deck, and then — all the cards from the beginning of the deck to the last card, equal to x, going to position p. Both cases are easy to process, if for each number write out all the positions of cards with such a number in ascending order. In addition, you need any data structure that allows you to count the amount on a segment and change it at a point, for example, if you store for each position 1, if the card is still in the deck, and 0 otherwise. For example, a tree of segments or Fenwick tree

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Didn't understand how to implement Fenwick trees here

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        My submission: Code

        1. store positions in the corresponding set v[val]

        2. iterate values through v[], if v[i] is not empty then binary search for the next element

        3. use the fenwick tree (which is global across all values) to calculate the amount of cards that are still active, which we would have to push it back to the bottom during the procss, and update it

        4. repeat step 2,3 until all elements are processed.

        → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    Actually, it can be solved much easier using two pointers: firstly, let's store the array of sets of the positions of some element x, so it would be something like this: in the array Pos the key is the card value, and value is set of the positions of this element. Also let's maintain a set of values(we will name it "values"), which are still left in our array. So now we do the following: while not values.empty(), we look to the last position of the minimum element in the array (*values.begin()) , and look to the next element in the "values". And if the last position of the minimum element in the "values" set is greater, than last position of the next element in "values" set(we can determine it with O(log n) complexity, using the lower_bound function), than we know, that after deleting the last element (*values.begin()) in the array we can not delete anything else, because the next element after *values.begin() always stands leftside from the current minimum element. So the size of the array decreases only by the size of Pos[*values.begin()].size(). If not so(if the last position of the minimum element in the "values" set is less, than last position of the next element in "values" set), than also with the lower_bound function we determine the first position of the next element in "values", that is greater, than the last position of the current minimum element in the array, and after getting the iterator on this element we start deleting all the positions from the set, that are greater, then the last position of minimum element.And we can see the case (ex.: 1 1 1 2 2) that after deleting the minimum element(x = 1) we can also delete all elements that are becoming minimum after x(in this example after deleting 1 we can delete all 2 elements), so we now with only one iteration through array we can delete more than one kind of elements, so we derease our length of array by the size of Pos[x].size() minimum elements x, that we can delete entirely, and by the amount of positions of the last minimum element we could not delete entirely. And before each iterartion we add the current size of the array. That's all:)

    Sorry if the explanation is some kind of vague, feel free to ask questions. Here is my code: 28526786

    → Reply
»
7 years ago, # |
  Vote: I like it +8 Vote: I do not like it

830A — Office Keys
"To solve this problem you need to understand the fact that all keys which people will take is continuous sequence of length n in sorted array of keys."
can anyone explain this , why it should happen ? How you get to know that you should sort them , any tips is really appreciated

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +4 Vote: I do not like it

    lets divide all man in 2 groups : left men and right man(if their poitions is right or left from office). It is obvious, that the "right" people should go right to the office and take all the keys on their way, it is true for the "left" people also. Of course we can face the situation , that the amount of keys on the way right to the office is to small, so each "right" man can take the next key to the right that is not take or, the next key to the left(if he will skipp one key, the overall distance will only increase).That is absolutely true for the "left" man too. So you can see that it should really be a continuous sequence. If you have any questions, feel free to ask. I hope thois will help you

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      sorry but it is not clear.
      Thanks for at least making effort , it is appreciated.
      It is a genuine doubt , i don't know why people are not asking and answering :p , seems like all follows intuition and don't care to prove anything.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Hm, can you try to explain, what is not clear?:)i'll try to explain one more time

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it +1 Vote: I do not like it

          Can someone help me in formally proving that the greedy way of having continuous assignment between the keys and people is optimum.

          Lets take a simple case of 2 people (p1 < p2) and 2 keys (k1 < k2).Let the position of office be O.

          We need to show that max(|p1k1| + |k1O|, |p2k2| + |k2O|) ≤ max(|p1k2| + |k2O|, |p2k1| + |k1O|)

          ie. matching p1 to k1 or p1 to k2

          Now we need to take care of 4 cases (LHS and RHS can have 2 possibilities each). But I couldn't get any useful information from this relation.

          I'm stuck over here . Is this way of proving wrong ?

          → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      I too,am facing the same problem,during contest I had the same intuition but it was too naive and had no backign up for it,also i was left with only 20 minutes,I came and checked the solution and I see the author's solution also mentions that,till now however I have not been able to prove why it is right..please help with the proof![user:VovanF98]

      → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I think intuitively, you could start by proving that what if the people did not take consecutive keys? If there was a key that was not used by anyone and the key is between two "continuous key parts", would it be better for someone to choose the key instead? In essence, proving by contradiction may be a good start.

    → Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Why should we put initial scores exactly in set in problem C div 2?

→ Reply
»
7 years ago, # |
← Rev. 3   Vote: I like it +19 Vote: I do not like it

Simple solution for div2 A:

Let make up 3 states: state 1 if a[i]  >  a[i - 1], state 2 if a[i]  =  =  a[i - 1], and state 3 if a[i]  <  a[i - 1].

Now init prev_state  =  1 and iterate in range [2;n]. If state  <  prev_state, output "NO", otherwise prev_state  =  state and continue iterating.

It looks really simple: http://codeforces.me/contest/831/submission/28547499

→ Reply
»
7 years ago, # |
← Rev. 8   Vote: I like it +17 Vote: I do not like it

Very simple solution for Div1 C.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    Could you please explain it in a clearer way?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      I think I can prove that his method is correct.
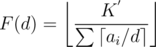      is an increasing function with d.
      We want the max value of d such that F(d) ≥ d
      For some d, let F(d) = x.
      If x < d then this d is invalid, but if x ≥ d then as F is an increasing function, F(x) ≥ F(d)
      We can say that, F(x) ≥ x, so x is a better solution.
      So for every d that satisfies F(d) ≥ d we have a better solution,
      F(x) ≥ x where x = F(d)
      Hence we need to check only on the possible values of F(d)

      → Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    I understand all your analysis, but when it comes to your code I got screwed up.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Check my submission: 28524841

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +3 Vote: I do not like it

        yep, I checked it and don't follow why all the possible answers are values of k/i

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
          ← Rev. 3   Vote: I like it 0 Vote: I do not like it

          There will be atmost O(2*sqrt(k)*n) values of floor(k/i). I am iterating on i in such a way that all possible value of floor(k/i) occurs once. Total number of iterations will be O(2*sqrt(k)) and complexity will be O(2*sqrt(k)*n).

          For more information: link

          → Reply
          • »
            »
            »
            »
            »
            »
            7 years ago, # ^ |
              Vote: I like it +3 Vote: I do not like it

            I understand that you are iterating through all possible values of floor(k/i). But why are they possible answers? why can't answer be sth like floor(k/i)+1 or floor(k/i)-1? U see that if d get smaller, it is more likely to become a valid answer. Thank you for your patience.

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              7 years ago, # ^ |
                Vote: I like it 0 Vote: I do not like it

              d*Σ (ai + d -1) / d <= k + Σ ai ;

              d <= ( k+ Σ ai ) / ( Σ (ai + d -1) / d ) ;

              The ( k+ Σ ai ) / Σ (ai + d -1) / d has at most sqrt ( k + Σ ai ) values.

              So it is enough to check all these values.

              I understand like this.

              → Reply
              • »
                »
                »
                »
                »
                »
                »
                »
                7 years ago, # ^ |
                  Vote: I like it +3 Vote: I do not like it

                The ( k+ Σ ai ) / Σ (ai + d -1) / d has at most sqrt ( k + Σ ai ) values.

                Yeah, but why can't d be a bit smaller than some value?

                → Reply
                • »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  7 years ago, # ^ |
                    Vote: I like it +3 Vote: I do not like it

                  Ok,i am confused now too,233. If you solve it, please remind me,555.

                  → Reply
            • »
              »
              »
              »
              »
              »
              »
              7 years ago, # ^ |
                Vote: I like it 0 Vote: I do not like it

              I still want the answer to this

              → Reply
              • »
                »
                »
                »
                »
                »
                »
                »
                7 years ago, # ^ |
                  Vote: I like it 0 Vote: I do not like it

                Nope, I still haven't come to a reasonable prove to it. Yet I do understand the method described by the editorial.

                → Reply
                • »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  7 years ago, # ^ |
                    Vote: I like it 0 Vote: I do not like it

                  I proved it in a comment above

                  → Reply
          • »
            »
            »
            »
            »
            »
            7 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            I got your analysis . but i am not getting how you are iterating over so that each value occur once and checking the condition on your analysis . can you please explain it

            → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In div-2 E — Cards Sorting, i am using segment tree to find out the remaining cards. My code passes the sample test cases of this problem but i am getting WA. Please have a look at my code here and please tell me how to correct it.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Your code works if all the cards all unique. This is because you are sorting them based on value. But what if some values are repeated ?. If you have two values which are equal to minimum and they are left and right of the card removed, you should consider the right one, which you cant guarantee by sorting.

    Instead try finding minimum in left half and right half separately using seg tree. Code

    → Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

[Div 2 C]

How do we take care of the fact that there can be upto 4 * 106 values in the set (i.e the number of possible initial values), according to the editorial solution?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    There are only at most 2000 score changes, so you have at most 2000 initial score to check

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it 
      set<int> initial_scores;
ll prefix_sum[2005];

for(int i = 0; i < n; i++)
{
   for(int j = 0; j < k; j++)
   {
      initial_scores.insert(b[i] - prefix_sum[j]);
   }
}

      Here the set can have up to 4 * 106 values right?

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
        ← Rev. 3   Vote: I like it +1 Vote: I do not like it

        It's enough to get the initial points only for b[0] (like in tutorial). The solutions should be among these values + prefix_sum[i]. points = b[0]; for(int i = 0; i < n; i++){ points = points — a[i]; initial_scores.insert(points); }

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Oh, how could I miss that! Thanks bagodabago and YTF!

          → Reply
          • »
            »
            »
            »
            »
            »
            7 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            I still didn't get it. Why should we take only b[0] for initial points. Please someone explain.

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              7 years ago, # ^ |
                Vote: I like it 0 Vote: I do not like it

              Let n = 6, a (jury points): 5 5 -15 -15 10 15 and b (points which he remembers): 100, 95, 90. pts = b[0] = 100. If he remembers after 1st jury the intial points are 95(pts = pts — a[0]). If he remembers after 2nd jury the initial points are 90(pts = pts — a[1]). If he remembers after 3rd jury the initial points are 105(pts = pts — a[2]). If he remembers after 4th jury the intial points are 120(pts = pts — a[3]). If he remembers after 5th jury the initial points are 110(pts = pts — a[4]). If he remembers after 6th jury the initial points are 95(pts = pts — a[5]).

              So the initial points that player had could only be 95, 90, 105, 120, 110, 95, although Polycarp couldn't remember that once the player had 100 points.

              You have to check that these points, and only these, are the solutions.

              → Reply
»
7 years ago, # |
  Vote: I like it +25 Vote: I do not like it

I completely don't get why scoring for D and E was 2250-2250. Maybe D is not easy, but is kinda standard and E is definitely not standard and demands a lot of work and not very pleasant code. 2000-2500 would do the justice. Results of both VK (known before round) and round itself confirm this.

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Could anybody tell me how to optimize this solution on Java? 28657960 (logical part in method "solve")

For start, I do so as it do in tutorial. It got TL on 7 test.

Then I change array to set. It got TL on 34 test.

Then I change long to int where it possible. It got TL on 36 test.

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In problem 830D in state “Take the root, and it combines two paths” i think we have to do this dpi, L + R - 1 +  = X·C(L + R, 2)·4 instead of dpi, L + R - 1 +  = X·C(L + R, 2)·2 ( 2 swivhes to 4 ) becuse we have 2 paths and these two path have 4 endpoints for each path we should pick one 2*2 and also when we take root and connect it to a path from left or right child if this path we choose is on vertex path we shouldnot multiple X.L by 2 becuse there is one end point only am i right ?

→ Reply
»
4 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

In problem div1 B it is "start viewing" and not "stark viewing". I got confused due to this and it took so much of my time. So I thought I should write a comment for someone who may also get confused.

→ Reply
»
3 years ago, # |
  Vote: I like it 0 Vote: I do not like it

2D DP solution for A. Office Keys in Python

Link

→ Reply
  • »
    »
    3 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Can you please explain how the solution works ? What is the state represented by dp[i] ?

    Why it is optimal to take a continuous sequence of keys as mentioned in the editorial ? "To solve this problem you need to understand the fact that all keys which people will take is continuous sequence of length n in sorted array of keys."

    → Reply
    • »
      »
      »
      3 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Hey Nimantha, You can refer this video solution, my solution is inspired from him only. Link

      → Reply
      • »
        »
        »
        »
        3 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Thank you. Actually I watched colin galen's video. I understand that two people can't choose keys such that they cross their paths.(This point is explained in that video) But I don't understand the reason for assigning people to a continuous sequence of length n of keys. Like if the first person is assigned to the ith key, the second person is assigned to the (i+1)th key, and so on.

        → Reply
        • »
          »
          »
          »
          »
          3 years ago, # ^ |
          ← Rev. 2   Vote: I like it 0 Vote: I do not like it

          This can be checked intuitively by taking an example. Suppose people stand on the points [1,2,3,4,5] and keys are placed on points [10,20,30,40,50].

          Then, you can try associating :- - Method 1 : (1, 30), (2, 10) and (3, 20) ; - Method 2: (1, 10), (2, 20) and (3, 30)

          Compute distances and compare. method 2 is optimal.

          → Reply
»
16 months ago, # |
  Vote: I like it 0 Vote: I do not like it

how to solve office keys with dp please

→ Reply
  • »
    »
    6 weeks ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    You can use a 2D DP to solve this, see my submission its pretty intuitive.

    Link to my submission.

    → Reply
»
6 weeks ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

DP solution for 830-A Office Keys.

Submission

→ Reply