Given a set of n integers S, with no elements divisible by n. Prove that there exists a subset of S that has a sum divisible by n. In this case, n should be > 1.
I'm pretty trash at mathematical proofs. Can someone help me out?
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | jiangly | 3976 |
| 2 | tourist | 3815 |
| 3 | jqdai0815 | 3682 |
| 4 | ksun48 | 3614 |
| 5 | orzdevinwang | 3526 |
| 6 | ecnerwala | 3514 |
| 7 | Benq | 3482 |
| 8 | hos.lyric | 3382 |
| 9 | gamegame | 3374 |
| 10 | heuristica | 3357 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 169 |
| 2 | -is-this-fft- | 165 |
| 3 | Um_nik | 161 |
| 4 | atcoder_official | 160 |
| 5 | djm03178 | 157 |
| 6 | Dominater069 | 156 |
| 7 | adamant | 154 |
| 8 | luogu_official | 152 |
| 9 | awoo | 151 |
| 10 | TheScrasse | 147 |
Given a set of n integers S, with no elements divisible by n. Prove that there exists a subset of S that has a sum divisible by n. In this case, n should be > 1.
I'm pretty trash at mathematical proofs. Can someone help me out?
| Название |
|---|



Arrange them in any order and look at prefix sums.
You have to consider the prefix sums, but I think that the key part of the solution is knowing Pigeonhole principle
Idea is like partial sum.Consider S1 = a1,S2 = a1 + a2,..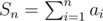 .Now we have n numbers (S1,S2,..Sn) and if one of them is divisible by n we're done,so asumme opposite.Now we have n number and less then n - 1 different remaniders modulo n so at least 2 of remainders (by PHP) are equal,let's say Si and Sj.But then n|Sj - Si.
.Now we have n numbers (S1,S2,..Sn) and if one of them is divisible by n we're done,so asumme opposite.Now we have n number and less then n - 1 different remaniders modulo n so at least 2 of remainders (by PHP) are equal,let's say Si and Sj.But then n|Sj - Si.