szawinis's blog

How to prove this?
By szawinis, history, 8 years ago, In English

Given a set of n integers S, with no elements divisible by n. Prove that there exists a subset of S that has a sum divisible by n. In this case, n should be > 1.

I'm pretty trash at mathematical proofs. Can someone help me out?

  • Vote: I like it
  • 0
  • Vote: I do not like it

»
8 years ago, # |
  Vote: I like it +2 Vote: I do not like it

Arrange them in any order and look at prefix sums.

→ Reply
»
8 years ago, # |
  Vote: I like it +3 Vote: I do not like it

You have to consider the prefix sums, but I think that the key part of the solution is knowing Pigeonhole principle

→ Reply
»
8 years ago, # |
  Vote: I like it +37 Vote: I do not like it

Idea is like partial sum.Consider S1 = a1,S2 = a1 + a2,..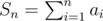.Now we have n numbers (S1,S2,..Sn) and if one of them is divisible by n we're done,so asumme opposite.Now we have n number and less then n - 1 different remaniders modulo n so at least 2 of remainders (by PHP) are equal,let's say Si and Sj.But then n|Sj - Si.

→ Reply