Приносим свои извинения за серьёзные неполадки с тестирующей системой в самом начале контеста. Мы надеемся, такого не повторится.
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...










По поводу задачи B... Можно решить проще: и по памяти, и немного по времени (вроде бы). Можно одним проходом по массиву найти 3 наименьших элемента и их количество, а потом 3-4 условия на то, что выводить (случаи, если наименьшего больше трех раз встретилось, и парочку, если наоборот).
Можно, конечно. По времени то же должно получаться. Решение из разбора разве что объяснять проще.
Thanks for fast editorial! :D An easy trick for D: Once you have calculated the sum of minimum in all subarrays, you can just make all the numbers negative ( multiply each of them by -1) and then again calculate the sum of minimum in all subarrays. The sum of maximum will just be the negative of that.
Thank u sir for enlightening us with such a good method!! Hats oFf!!
C problem also solvable with DP (27810451) works in 183 * 92 * 2.
D problem also solvable with D&C approach(27810683) which works in N * log(N).
Can you explain your dp states for Problem C ?
dp[position in decimal representation][equal or not][sum of digits]
what is the D&C approach?
why did this DC solution 27820818 get MLE? could you explain it to me please?
hehe inline??????? http://www.cplusplus.com/articles/2LywvCM9/ passed my solution
Can you please elaborate what is your approach, it is interesting.
D problem D&C aprroach link
This implementation is same as of Kerim.K , just some comments added for ease of understanding.
Thanks to Kerim.K for sharing the approach...
You've explained it very well.
Альтернативное решение C:
Заметим, что все числа, меньшие s — не действительно большие. Рассмотрим число x >= s. Очевидно, x — сумма_цифр(x) >= x — максимальная_сумма_цифр = x — 9*18 = x — 162. Тогда, если x >= s + 162: x — сумма_цифр(x) >= s + 162 — 162 = s, то есть число действительно большое.
Значит, количество НЕ действительно больших чисел от 1 до n равно:
X = кол(<s) + кол(>=s) = min(s-1, n) + (кол-во не действительно больших чисел на отрезке [s, min(s+161, n)]).
Ответ на задачу равен n — X.
There is also another solution for problem C.
Since we know that the maximum value for n is 1018, then the maximum sum of digits we can get is for n = 999999999999999999, which is 162. Using this observation, and the proof mentioned in the editorial, we can be sure that all integers in the interval [s + 162, n] are really big numbers. So, what is left now is to check the interval [s, s + 161] with a simple for-loop.
#include <bits/stdc++.h>
define ll long long int
using namespace std;
int main() {
}
Amazing observation :D
Can i know the difficulty difference between an educational round and a normal round.How does difficulty of each problem in Normal round map to educational round?
It's usually like a standard div2 round + one task slightly harder than div2e.
E and D are good so that people can learn something new from the contest. Though they were standard trie and stack questions . I felt they were educational.Hope u introduce more advance concepts and data structures through educational rounds.
I did not understand the editorial to problem B. please explain. thanks :)
A very simple approach to problem B: Sort the array containing the numbers. Pick the first three. Now, we can prove that the minimum product will always contain only these three elements and nothing else. Thus, we next count occurrences of these first three letters in the whole sequence. Let the first, second and third numbers be a, b and c. And their repetition in the whole sequence be countA, countB, countC, and let they all be different. Then, ans is countA*countB*countC. But, if b repeats, then b is equal to c (sorted order). Then ans is countA* (ways of choosing 2 elements from countB elements). Similarily if a is repeated two times. Ans is countB only(any other repetition of a will cause it to be equal to c). If all three are same. Then ans is (no. of ways of choosing 3 elements out of countA elements). Here, the no. of ways of choosing 3 elements out of n elements = n*(n-1)*(n-2)/6 Here, the no. of ways of choosing 2 elements out of n elements = n*(n-1)/2
I did the same thing for B, but I keep TLE-ing on test 43. I'm convinced there's some kind of error in the judger or the data, because every other test takes less than 200 ms, including the 100000-length ones. I even bit the bullet and used BufferedReader instead of Scanner...no difference.
Take a look at my submission. Can you see some weird degenerate case that would cause my solution to not be O(NlongN + N)? I'm going crazy over here!
solution
check it out..this might help.
Can you please explain why the number of ways to choose 3 elements out of n is n*(n-1)*(n-2)/6 ?
I am not getting problem A ,I mean why does not (x2-x1)%x==0 and (y2-y1)%y==0 work?Please explain.
it works but you also have to check if it's possible to reach the point doing movements in L. like a horse on chess. It will be reachable if the number of moves performed in the x axis + the number of moves performed in the y axis is even. This happens because when you move, you always do a move in both axis.
but also number of moves in x and y-axis can't be given by (x2 — x1) / x, (y2 — y1) / y because in 0 0 0 6 and x=2,y=3,no of moves in x axis is not(0-0)/2
So what? Yes, it isn't 0, but we only care of the parity of this number and (0 + 0)/2 + (0 + 6)/3 is even, so the answer exists.
How to approach a problem like 'B'? I mean how does the right technique strike? Are there any pointers(in the limits or similarity to a classic problem) to the right way? Any help would be appreciated.
Hmm. I don't really know :) I used the approach from the editorial in couple of other problems, though I can't remember any in particular. I guess that if this one doesn't seem intuitive then you can always try the other one. Where you just check some cases on the amount of the elements less than the third minimum of the array. Most people implemented this solution.
UPD: the author of this task told me that the similar approach is used here
Thanks a lot, awoo.
i would request the author to provide the implementation described in the editorial Thanks for the help awoo Also i have seen many people doing sorting will that not affect the ordering (i<j<k) as described in the question???
ordering will not be affected because if there is 3 indices in sorted array then there will be 3 indices in previous array. Isn't it .
Here it is.
Reorders will not affect answer. Why should they? You will just take the same triplets but indices in each will be in other order.
I solved it differently. First sort array a. Then take three smallest values, let them be a,b,c in this order. Also, while doing input of array, keep array cnt[x], which tells how many times x appeared in input.
That covers all cases.
Can you explain how did you get these formulas?
marginal You may see these formulae as "n choose r". If we denote this value with the function c(n,r), c(n,r) = n!/(r!(n-r)!). So here, in case 1: It is simple product-rule of combinatorics case 2: It is c(cnt[a],2) that we need; because that gives us the number of ways to choose a(and hence, b). case 3: Like case 2. case 4: It is c(cnt[a],3). Hope this helps.
True. The condition i<j<k made me think that sorting would be of no help . This is may be because I assumed that a[i]<a[j]<a[k] which is not so. Need to practice more. Thanks
Hello, In problem D I don't know why did I get a Wrong answer on test 12. Can you please help me?
27814997
I guess integer overflow in the last for loop
How to solve the problem D when imbalance is defined as (max-min)^2 or (max-min)^k with k>=2 in better than O(N^2)?
WHat is the movement of
source: 2 -5 destination: -8 8
move: 2 1
. in Problem A ? How this is YES ?
0 -4, -2 -3, -4 -2, -6 -1, -8 0, -8 1, -8 2, .. .. .., -8 8
(-2,+1) (-2,+1) (-2,+1) (-2,+1) (-2,+1) (+2,+1) (-2,+1) (+2,+1) (-2,+1) (+2,+1) (-2,+1) (+2,+1) (-2,+1)
Why my MEX queries does not work? Here's my code:
aren't NlogN solutions supposed to pass for D ?? Mine got TLE because it uses insert and lower_bound in a set n times ! and I know their complexity is logN http://codeforces.me/contest/817/submission/27808174
I also have the same problem...
Here is my code.
NlogN solutions were supposed to pass but in your solution the constant factor is large (around 5).
In your code the complexity is :
Overall Complexity — 5*NlogN (Worst Case) = 5*(10^6)*(20) = 10^8.
And only those O(10^8) solutions pass in 2 sec which are highly optimised. In your case the hidden constant factor of set insertion also affects your code complexity.
Other NlogN solution which passed : 27810683 by Kerim.K
I solved Problem C by searching for the first 'Really Big Number' greater than 's' and less than or equal to n by running a loop.I considered the fact that if a number suppose i=25 doesn't satisfy the 'Really Big Number' condition then no number from 20-29 will satisfy the condition and thus I can jump from i=25 to i=30.By following this, if i found the first valid number less than or equal to n then our answer will be 'n-i+1' otherwise '0'. My question is whether my approach is correct or not because i got accepted but i couldn't proved why my approach is correct. Here is my accepted code.
Your approach is absolutely correct since you have used binary_search.
As you can observe from the value of num-sumD(num), it is always increasing.
And since the value of num — sumD(num) is strictly non-decreasing, take the lower limit to be 1, higher to be n + 1 and search for the appropriate num such that for values less than num (num — sumd(num)) is less than s and for values greater than or equal to num (num — sumd(num)) is greater than or equal to s.
So your approach is alright. For more clarification you can see my code : 27802867
I don't know where I went wrong in problem C please help I don't know much about dp and stuff I used the fact that difference of any number and its sum of digits is equal to nearest multiple of 9 of that number.
This is for itachi_2016's approach.
Try the following test case and you will realize your mistake.
109 91Can anyone help me with sqrt decomposition solution for 817F - MEX Queries (According to editorial its possible).
I can't figure how this approach can be used to solve Problem F.
It's not much different from the segment tree one. Numbers are also compressed and the queries are the same.
You process assigning on a segment and xor of the segment by dividing original array into sqrt blocks, for each block you maintain its sum. Lazy propagation is used too. Just every query works in instead of
instead of 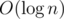 .
.
We decided not to force participants to use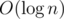 solutions.
solutions.
Lazy propagation in sqrt decomposition? Anyone has some resources for that?
Similar problem as D are :
http://practice.geeksforgeeks.org/problems/maximum-of-minimum-for-every-window-size/0
http://agc005.contest.atcoder.jp/tasks/agc005_b
Same approach can be use in these problem , next smaller , next greater using stack .
Can someone please tell why my code is getting WA ??? Link .Thanks in advance !!!
your code is giving wrong answer because suppose you are standing on a node where xbit=1 and ybit=0 then there xor is 1 and you are adding all the numbers that have that bit zero. but this is wrong because this does not gaurantee all the number in this group to be smaller then your leadership(l).this group till now are only equal, not became less. so you can't add them. if xbit=0 and ybit=1 then your case is correct. there may be case some of these number can latter become equal to or greater than leadership(l). link this is my code you can see . this might help you visualising what i am saying.
Problem B In the tutorial "Let's also store set of three elements which give minimal product of the array". In c++ how do you calculate the product if all the numbers are greater than 10^9?
Скажите, а что делать, если в задаче Е нет числа p[i] ^ l[i]?
Problem B In the tutorial "Let's also store set of three elements which give minimal product of the array". In c++ how do you calculate the product if all the numbers are greater than 10^9?
hi
we don't calculate product of three numbers
and question is "how many ways are there to choosing three minimal numbers"
because minimal numbers give us minimal product
There is also one more solution of problem C.
All numbers bigger than s+9*18 and not more than n are really big. So we can check numbers from s to s+9*18 and add max(0, n — s-9*18) to answer. Sorry for my English
Problem F in such constraints can also be solved with coordinates compression and bitmasks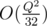 in obvious way.
in obvious way.
BTW, it's fastest solution at this moment. (171 ms without fastIO). 27832302
can you explain your approach . it is diificult to understand from code
Global idea as it is in the editorial:
Let's store this array of zeros and ones as bitset, it means that each byte of array will represent 8 values in 8 bit. Then you can perform first two queries on 32 values at once as simple assignment of int variable a[i] = 0 or a[i] = -1, and third query as a[i] = ~a[i]. To find the answer after each query you should find first value in array not equal -1 and find first zero bit index in it.
Can anyone explain me D&C solution for D? Because solution with stacks looks awful. I was thinking D&C on contest but couldnt solve it. Edit: got it. this solution helped me http://codeforces.me/contest/817/submission/27832753
Detailed approach for D???
Considering finding the sum of minimum values for all subsegments, the solution tries to know for each index i how many times a[i] will be the answer. If x is the number of subsegments that contain index i and a[i] is the minimum value, then ans[i] = x·a[i]. The final answer will be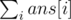 .
.
For the correctness of the algorithm, if a subsegment have more than one cell with the same value, we will consider the answer to be the leftmost cell.
For index i, Let:
Clearly, All cells in the range [L[i] + 1, i - 1] have values greater than a[i] and all cells in the range [i, R[i] - 1] have values greater than or equal to a[i]. Now, we can say that index i can be the answer to any subsegment whose startpoint is in the range [L[i] + 1, i] and endpoint is in the range [i, R[i] - 1]. So, ans[i] = (i - L[i])·(R[i] - i)
How to compute the array L? Keep a stack with you and go from left to right. The stack is initially empty and will contain indices. Now, we are at index i:
If j is popped from the stack, then for k > i, can L[k] = j? The answer is no, because a[j] > a[i] and i is closer to k from j, so if a[i] ≤ a[k], then L[k] = i. Otherwise, a[j] > a[i] > a[k]. That's why we remove j from the stack because it will never be used again.
After finding L[i], push i onto the stack.
You can compute the array R in a similar way from right to left.
Shouldn't the L array be calculated on right of i'th element instead of j < i and similarly for R array , If I'm wrong correct me , you are trying to calculate for each i'th element the no of elements which are lesser than a[i] to its left and right (to whatever position we can extend the left and right boundaries )
The objective is to find, for each index i, the closest element to its left side that is not greater than ai, and similarly to the right side.
Can any one tell me why we are doing mod 2 in problem A.
hi
it is difficult to explain but
if there modes in 2 aren't equal then we can't arrive from x1 to x2 and y1 to y2 in the same time
and if there modes in 2 are equal then imagine that:
x2 > x1 and y2 > y1 and (abs(x2 — x1)/a) > (abs(y2 — y1)/b)
then you can simply do x1 + a, y1 + b and x1 — a, y1 + b k times and you will have
(abs(x2 — x1)/a) and (abs(y2 — y1) + b*2k)/b
and you can chose correct k to get (abs(x2 — x1)/a == abs(y2 — y1)/b + 2*k) because their modes in 2 are equals.
for another cases you can do like this.
if mod 2 is 1, then we can reach target with odd number of moves. Otherwise, we can reach target with even number of moves. So, the parity (odd/even) must be the same for both horizontal and vertical moves.
can you explain the logic of problem D. I have read it many times still it fails to strike me . I understand upto how to calculate left[i] and right[i] after that how he is finding no of segments and rest of solution. please help
Check this comment
Can anyone explain Problem D?? I read the solution many times but not getting it.
Check this comment
Is there an online solution for F ?
I thought of having a sorted set of ranges . Insertion and deletion can be done in O(qlog(q)) amortised time . But I'm not sure how to implement flipping efficiently .
You can use Dynamic Segment Tree.
I've tried to do it, but got Memory Limit Exceeded. I think my implementation is still not good enough. If you want some idea on how to code, this is my code: 27989735
I think that I would receive Accepted if memory limit was higher.
Can you please briefly explain your approach.
Imagine that you will solve this problem with a standard segment tree with range update (10^18 nodes and lazy propagation).
The only thing that change in the dynamic segment tree is that you do not declare an static array with size 4 * 10^18, you just create those nodes that you really need to, because there will not exist 10^18 queries.
Here is an example, if you do not have any query in range [10^5, 10^10], simply don't create those nodes.
And if you want to flip some interval [l, r], just do this:
How is the complexity for B (as per the solution given in editorial) is O(n)? How will you find the 3 smallest no.s in O(n), i.e without sorting( which would take O(nlogn) )?
hi
you can save 3 smallest numbers in 3 Variable and save their count
even it isn't necessary to store all numbers.
Can someone please tell why my code is getting WA at test 12? Link Thanks in Advance!
There was overflow in some operations (maybe l * r), here is your code without overflow: 28011406
Anyone there who can help me with my previous post. Please help me. Don't know what is the problem with my code. Why my code gives tle in 43th test case.
I'm not sure but this can probably be Java anti-sort test. Arrays.sort over an array of primitive types uses quicksort and may work in O(n2). Try replacing it either with Collections.sort or with array if Integer values.
Что измениться в задаче Е если будет ограничение pi^pj <= l а не pi^pj < l ???
I am getting WA on test case 7. Can anyone tell me which case I am missing??? The method I used to solve this problem is almost identical to the editorial... I just put the values L and R+1 in a set and then constructed segment tree from there... Any help is appreciated. :)
Chtholly Tree used to solve F: 88862104
You can solve the 817B using one traversal instead of two. Simply store the numbers inside a
std::map, whose keys are by default sorted ascending. Then there are only a few cases:Assuming the frequency of the smallest 3 elements are respectively
a,b,c:if
a>=3, the answer iscomb(a, 3)if
a==2, the answer isbif
a==1 && b==1, the answer iscif
a==1 && b>=2, the answer iscomb(b, 2)Don't understand editorial for E, can someone explain it more detailedly?
Thanks a lot in advance.