Задача А:
Заметим, что в конец копируется элемент, который был k-тым. Затем копируется элемент, который был (k+1)-м в исходном массиве, затем (k+2)-й, ... , n-й, k-тый, (k+1)-й etc. Значит, все числа станут одинаковыми тогда и только тогда, когда в исходной последовательности все числа с k-го по n-й были одинаковы. Теперь очевидно и то, что количество операций, требуемое для этого, равно номеру последнего не равного n-му элемента последовательности, так как ровно столько удалений понадобится для того, чтобы убрать не равные ему элементы. Если этот номер больше, чем k, то ответа нет. Асимтотика — O(N).
Задача B:
Давайте на каждом шаге будем хранить текущий порядок строк и порядок столбцов в таблице, относительно начального. То есть, row[x] — номер строки x в начальной таблице, а column[x] — номер столбца x в начальной таблице. Тогда значение элемента в строке x и столбце y текущей таблицы будет равно t[row[x], column[y]], где t — начальная таблица. В запросах обновления нужно просто поменять местами ячейки соответствующего массива с номерами x и y. Асимптотика O(n * m + k).
Задача C:
Для начала факторизуем числитель и знаменатель. Теперь для каждого простого числа x мы знаем степень этого числа в факторизации числителя(a[x]) и в факторизации знаменателя(b[x]). Для любого простого числа x мы можем вычислить его степень в факторизации числителя числа после сокращения(newa[x]) и в факторизации знаменателя этого числа(newb[x]): newa[x] = a[x] — min(a[x], b[x]), newb[x] = b[x] — min(a[x], b[x]). У нас есть числитель и знаменатель ответа(в факторизованном виде), осталось только привести их в вид, требуемый в условии. Один из способов — заметить, что дробь из условия подходила под все требования. Поэтому можно факторизовать ее еще раз и вывести такую же дробь, но так, чтобы ни одно простое число не имело большую степень, чем в посчитанных нами newa и newb. Получившиеся числа будут подходить под ограничения и их частное будет равно искомому числу. Если пробовать строить ответ жадно (набирать множители, пока их произведение <= 10^7), то количество чисел в ответе выходит за рамки 10^5. Асимптотика решения O(max + n * log max). Факторизация за O(sqrt(max)) получала TL, поэтому нужно было воспользоваться более быстрыми способами. Например — посчитать для каждого числа его наименьший простой делитель с помощью линейного решета эратосфена.
Задача D:
Во-первых, заметим, что наилучшее место, которое мог занять Вася — это первое, ведь ограничений сверху на его балл нет. Теперь нужно найти самое худшее место из тех, что он мог занять. Переформулируем. Нужно максимизировать количество таких участников, что если участник в первом туре набрал a[i] баллов, во втором — b[j], то a[i]+b[j] >= x. То есть, нам нужно найти максимальное паросочетание в двудольном графе, в котором ребро между вершинами i первой доли, j второй доли есть тогда, когда a[i] + b[j] >= x. Для решения этой подзадачи достаточно было отсортировать вершины в обоих долях по весу, и пройтись двумя указателями. Допустим, мы отсортировали по убыванию веса. Возьмем два указателя L = 1 в левой доле и R = N в правой доле. Пока a[L] + b[R] < x (то есть нет ребра L->R) нам стоит уменьшить R — взять вершину во второй доле с большим весом. Как только мы нашли R такое, что a[L] + b[R] >= x, мы берем ребро L->R и добавляем в ответ. Все — переходим к следующим L и R. Несложно показать, почему этот алгоритм найдет оптимальное решение. Я нашел поистине удивительное доказательство этому, но поля этого разбора слишком узки для него. Асимптотика — O(N log N) на сортировку и O(N) на два указателя.
Задача Е:
1) Решение за O(n*m*m): Простая динамика. Состояние — d[n][m] — сколько возможных цепочек длины n могут заканчиваться на символ m. Переход — перебираем все возможные символы, и смотрим, можно ли поставить символ k после символа m.
2) Решение за O(m*m*m*log n): Заметим, что в нашей динамике переход всегда одинаковый. Можно составить матрицу перехода A размером MxM. Если jый символ может идти за iым, то A[i][j]=1, иначе A[i][j]=0. Пусть есть вектор размером 1хМ b={1,1,...,1}. Тогда можно заметить, что b * a^(n-1) = ans. Воспользуемся бинарным возведением в степень для того, чтобы посчитать a^(n-1). Отдельно следует рассмотреть случай n==1. Ответом будет сумма элементов в векторе ans. Асимптотика — m^3 на перемножение матриц и log n на бинарное возведение в степень.











Ахаха, классно!
Капитанское пояснение, для тех, кто не в теме: примерно это написал Ферма вместо доказательства своей великой теоремы.
И все-таки написал бы кто-нибудь доказательство, не могу понять почему данное решение верно :(
Оптимальность этого алгоритма заключается в его жадности: Без ограничения общности можно считать, что пары мы будем выбирать в порядке уменьшения первого элемента. Если предположить, что на каком-то шаге мы отклонимся от нашего алгоритма, то множество доступных чисел на следующем шаге будет не лучше, чем при выборе по нашему алгоритму ( в дальнейшем — "правильный" выбор). То-есть:
1)Если на каком-то шаге мы пропустили элемент из первого множества, то этот элемент станет недоступным на следующем шаге (так как мы выбираем пары в порядке уменьшения первого элемента), а число доступных и наибольший доступный элемент будут не больше, чем при правильном выборе.
2) Если на каком-то шаге мы взяли не наименьший возможный элемент из второго множества, то на следующем шаге, доступные элементы из второго множества, будут не больше, чем соответственные доступные элементы при правильном выборе.
И так как, полученные в итоге (при отклонении от алгоритма) множества будут не больше, чем при правильном выборе, то и пар в последствии мы сможем выбрать не больше.
Вот и всё. Следует только уточнить, что сравнение множеств в этот доказательстве выполняется, за счёт того, что сравниваемые множества отличаются не более чем на 1 элемент, соответственно результат сравнения множеств = результату сравнения этих не совпадающих элементов. Вот так вот.
Как второе доказательство могу предложить то, что любое множество пар удовлетворяющих условию можно трансформировать в пары, такие что первые элементы их будут идти по убыванию, а вторые — по возрастанию. (как именно, не буду расписывать; но для этого достаточно рассмотреть всего-лишь 2 пары). И эти полученные пары тоже будут удовлетворять условию. А наш алгоритм — оптимальный, потому-что выбирает наибольшее число пар с данным свойством.
Отдельно следует рассмотреть случай n==1.
Зачем?
Чтобы не думать, надо ли его отдельно рассматривать.
ок
Но бывает, что необходимость отдельно рассматривать что-то сигнализирует о неправильном решении. Может лучше убедиться, что оно не является частным случаем?
Скорее дело в том, что именно в этом решении матрица возводится в степень n-1. Чтобы не писать if на то, что есть матрица a^0, можно написать проверку на n == 1.
A^0 — единичная матрица, дающая верный ответ.
Извините, пожалуйста, может мне кто-нибудь по-подробнее рассказать, в каких случаях можно решить рекурентную последовательность с помощью возведения степень матрицы? Первый раз с таким случаем столкиваюсь, раньше встречала только задачи вроде Фиббоначчи или ввиде суммы предыдущих значений. Если у кого есть что почитать или ссылки на задачи, можете скинуть?
Решать рекуррентные формулы с помощью возведения в степень можно лишь тогда, когда их можно представить в виде суммы:
Такой вид называется линейно-рекуррентным. Эта формула аналогична вот этой:
Обозначим матрицу слева от равенства за Ψn. А квадратную матрицу за Q. Тогда перепишем нашу матричную формулу в таком виде:
Ну и возводя Q в различные степени, моно получить:
, где Ψm + 1 — вектор начальных значений нашей рекуррентной формулы. Пример (Фибоначчи):
Используя алгоритм быстрого возведения в степень, можно решать эту задачу за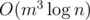 .
.
Но задача, которая была на 137, немного отличается от решения ЛРС. Там надо заменить Q на матрицу смежностей. А Ψm + 1 на вектор единиц Подробнее тут. Ещё про решение ЛРС можно прочитать этот пост на хабре.
P.S. Первый раз пишу формулы в latexe, сильно не убивайте.
спасибо огромное
Задача С. WA6. Такое решение. Находим сначала минимальную сумму. Сортируем массив В. Проходим по А, на каждой итерации бинпоиском подбираем значение из В. Сохраняем текущий минимум и сравниваем его с общей минимальной суммой. И соответственно сохраняем индексы из А и В. Потом удаляем соответствующие элементы из А и В. Сортируем по убыванию полученные массивы. И потом в цикле набираем места до тех пор, пока А[i]+B[i]>=minSum.
P.S. Сори, я про задачу D
В задаче E — 1 ≤ n ≤ 10^15 Решение за O(n*m*m) это как? O_o
Это динамика, которая была слишком медленной.
Оно приведено просто, чтобы из него дойти до правильного решения
что помешало написать такой же вывод как на е-максе? Там же все гораздо проще и яснее
к задаче Е — сложность в решение 1) O(n*m*m) — не слишком много если 1 ≤n ≤ 10^15...)
Зачем в C по TL класть факторизацию за корень? Просто тогда это уже не C получается, а минимум D, а то и E. Upd. У меня зашло с предподсчетом простых до корня, но 1980 мс — это стремно.
у меня за 1090 мс. Такое же решение.
1980мс — это вообще с большим запасом. 3065384 — вот это четкое попадание в ограничения.
Кстати, мое решение получилось идейно похожим на решение в разборе — думаю, его можно ускорить довольно заметно, если не делать "повторной факторизации". Не пожалеем немного лишней памяти для того, чтобы запихнуть туда все факторизации, полученные вначале, и не считать их второй раз в процессе сокращения.
upd: 3065521 — удалось срезать 0.15 секунд приемом, описанным выше. Не впечатлило. При этом понял, что первое решение вообще чудом работало — с циклами вроде
for (int i=1;i<=...;i++) {for (int i=1;i<=...;i++){}}
Может мне кто-нить объяснить почему эта посылка 2120846 получает такой исход? Не пойму все же.
строка 103, заменить вторую n на m
Мда, обидно((
здравствуйте. можете мне объяснить почему эта посылка зашла http://codeforces.me/contest/222/submission/2128719 а эта нет http://codeforces.me/contest/222/submission/2109395 ?
После
inc(cnt[a[r+1]]);нужно поставить такое условиеif (cnt[a[r+1]]=1) then inc(allcnt);Когда число появляется снова, ты не учитываешь его в общем количестве.2111813 на FPC проходит, а на Delphi — нет? У меня на компе все нормально работает.
Объясните, пожалуйста, почему в задаче С можно генерировать простые числа до 3163?
Потому что либо число делится на одно из них, либо оно само простое.
Может кто-нибудь помочь, почему такое решение по E 2143573 получает TLE, хотя вроде бы похожие решения проходили?
Отправь под free pascal ;)
Спасибо, прошло=) И в чем же дело?
Не знаю :) Но часто бывает, что один и тот же код под разными компиляторами работает разное количество времени. А в этом конкретном случае может кто-нибудь другой объяснит в чем дело.
Деление int64 в Delphi очень тормозит
У меня (задача E) один и тот же код на
Delphi4050 мс, а наPascale530 мс работает. Забавно:)For problem D:
Observation: we can try change matching to include any element (Proof: if element a isn't in optimal matching, but exist element b, that a + b >= x, we can add pair (_a_, b) to matching (possibly instead of previous pair with b)).
So we can simply check for all elements from A if there exist large enough element in B (and erase it from B). We should take smallest possible element from B of course.
My solution as examlple: http://codeforces.me/contest/222/submission/2115578
Author makes us smile with: "I have discovered a truly marvelous proof of this, but the margins of this analysis are too narrow to for him".
For the people who don't know about this line, it is related to Fermat's Last Theorem.
I can't understand how the first solution for Problem E can work. since n can be 10^15 and O(n * m * m) will surely get TLE for this n. wont it?
Задача В.
http://codeforces.me/contest/222/submission/2156849
Это нормально, что заходит существенно асимптотически неверное решение? Причем без особых оптимизаций.
P.s. автор решения — Ghella
Ну во первых О (5 * 10 ^ 8) на кф заходит в 3 секунды. Во вторых — в этом решении есть 2 оптимиза :
1 — Самописный swap.
2 — Вывод ответа в оффлайне, что быстрее, потому что мы обращаемся к элементу одномерного массива, а в онлайне лезли бы в матрицу.
Ну как-то так.
Я уже начал было писать, что мы так и так лезем в двухмерный массив, когда записываем очередное число ответа, однако: 2157583. Как это объяснить?
P.S.
std::swapдля базовых типов реализован точно так же (как ещё?).1 — это не оптимизация. Это решение на Си, отправленное под С++.
2 — Согласен с сообщением выше, мы и так лезем в этот двумерный массив. А по поводу того, почему не заходит — это как повезёт. На контесте почти это решение упало на 12 тесте (который входит в претесты, но претесты оно прошло). Когда отправлял его же в архиве — упало по времени 36-м тесте. Занёс объявление индекса для цикла внутрь for — прошло.
P.s. хотя действительно странно... Видимо, какие-то тонкие параметры оптимизатора.
Это традиция.
В 4C - Система регистрации заходит квадрат на длину строки 20030.
Но при этом люди жаловались, что не заходит верное решение. Это как-то по меньшей мере нехорошо.
Ну это ещё ни о чём не говорит. Есть запуск, где всегда можно проверить.
Плюс не понимаю, что верного в решении, получающем вердикт, отличный от AC?
Actually considering the case n=1 as a separate case is not necessary as we can start the multiplication from the identity matrix. In that way we can call a function solving the problem without any restrictions as n=1 and thus there is no need to consider the case separately.
for problem E, can anyone explain me the logic of why we can represent the problem as matrix exponentiation?
for problem E, can anyone explain me the logic of why we can represent the problem as matrix exponentiation?
Suppose we have computed the number of valid sequences of length n for any pair of beginning and trailing characters. We store this in old[i][j]. Now we want to compute the same result, new[i][j], for length n + 1. You can see that
where f(k, j) = 0 if the pair is forbidden and f(k, j) = 1 if it is not. Now, this is precisely the definition of multiplication of the matrix old by the matrix formed by f. It remains only to find a starting matrix that describes the n = 1 case, and repeatedly multiply it by f.
Thank you very much for this nice explanation.
isn't problem "B. Cosmic Tables" incorrectly worded?
the description says that n is the number of columns, and m the number of rows.
yet the tests don't work that way as test 4:
there is 1 column with 2 rows. yet the first statement is to swap column 1 with column 2.
how is that possible?
No, there are 2 columns and one row. Pay attention that the first number is a number of rows and the second — number of columns. So I guess there are no mistakes here
I failed at test case 42 .
How to solve C??
my solution gives more than 10^5 number.
I used factorization method of every number.
May be It is the wrong process>
but I don't understand the editorial.
plz somebody help me .
same here :(
How come my solution is showing TLE in qestion B? My logic is same as that in the tutorial. My solution --> https://codeforces.me/contest/222/submission/74291671
Proof of problem D anyone?
For problem B: my code is https://codeforces.me/contest/222/submission/86359093 can anyone suggest how to overcome TLE??
It seems impossible, the servers have changed since the problem was written.