Народ, нужна помощь. Решал задачу на Timus. 1011 Кондукторы Your text to link here... так вот не пойму почему она работает с типом Extended и не работает с Real.
Задача Какое может быть минимальное число жителей города, где кондукторы составляют строго более P%, но строго менее Q% населения? Ограничения: 0.01 ≤ P, Q ≤ 99.99. Числа P и Q могут быть заданы с точностью до сотых долей. Исходные данные Числа P и Q в десятичной записи, разделённые пробелом или переводом строки. Результат Программа должна выдать искомое число в десятичной записи. Вот собственно код program Pr; {$APPTYPE CONSOLE} var P,Q: Extended; min: Integer; i:Integer; Begin Read(P,Q); i:=0; while True do begin i:=i+1; min:=Trunc(P*i/100)+1; If min<Q*i/100 then break; End; Writeln(i); End. Помогите понять











Ну, подробно я не исследовал, но вообще-то известный прикол, что просто чтение десятичной записи с несколькими знаками после точки уже может дать погрешность. Например, в http://ejudge.sumdu.edu.ua/pdf/problemset.pdf задача B математически совсем элементарна
floor((a+b)/c), но именно так и написать не работает не только в double но даже и long double.Это было "Кто виноват?", а теперь "Что делать?" (если б просто переход к extended не помог).
Надо или работать исключительно с целыми числами (в том числе и читать в целые числа, или в строки и превращать их в целые числа вручную, хоть и не удобно), или как-то осмысленно играться с "эпсилонами" и сравнениями, в стиле приблизительно
min:=Trunc((P+1e-6)*i/100)+1; If min<(Q+1e-6)*i/100 then break;UPD надо играться, точно ли именно
+1e-6а не-1e-6, не уверенНикогда не используй тип real. это вообще какой-то искуственный тип, операции с которым реализованы программно, а не "железно", как в случае float, double — операции с этими типами умеет делать процессор (в стародавние времена это был арифметический сопроцессор). extended и long double для тех компиляторов которые с ним работают, тоже реализованы 'железно', но утверждать не берусь. В общем тип real очень медленный, и обладает меньшей точностью чем double. Для всех перечисленных типов верно то, что число представляется в двоичном виде, а теперь попробуй перевести число 0.2 в двоичную систему.
Чтобы найти конкретные числа просто пусти два цикла по всем возможным входным данным, и сравни результат работы двух функций, с real и extended.
Пожалуйста, переименуй тему в "Timus задача 1101 Conductors", будет видно что речь о конкретной задаче а не о тимусе вообще
UPD Разумеется, 1011 а не 1101
Что не работает идея с эпсилонами при double, real.
program Pr; {$APPTYPE CONSOLE} var P,Q: Double; min: Integer; i:Integer; Begin Read(P,Q); i:=0; while True do begin i:=i+1; min:=Trunc((P+1e-6)*i/100)+1; If min<(Q+1e-6)*i/100 then break; End; Writeln(i); End.
писал и +1e-6 и -1e-6. И с разными порядками. может я что не так делаю?
В конце концов можно. Например,
таки засчитывается. Задним умом даже понятно, почему именно так: нам надо строго меньше и строго больше, в том числе и нельзя чтоб были равны; поэтому к тому, что должно быть меньше, надо прибавить эпсилон (если меньше даже после прибавления эпсилона — значит, таки действительно строго меньше), а из того, что должно быть больше — вычесть.
Это задача 1011, а не 1101.
Я, успев наслышаться о такой проблеме, вообще рациональные дроби туда сдал :)
а как реализовать рациональную дробь? Будьте добры, приведите пример кода
Ну заводим record / struct / class с двумя полями: числитель и знаменатель. При создании новой дроби всегда делим числитель и знаменатель на gcd, чтоб поддерживать ее в несократимом виде. А вычисления понятно как делаются, это едва ли не в начальной школе проходят.
у меня в школе не было программирования... Была сплошная теория информации) я пришел в универ и знал уже что такое энтропия, формулу Найквиста ну все такое)) Нахождение же общего делителя разве позволяет тут уложиться по времени?
Я имел в виду, что сложение / вычитание / умножение / деление / сравнение / округление вверх / округление вниз рациональных дробей проходят в школе.
Например,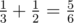 . Не было такого разве?
. Не было такого разве?
А делить на gcd хорошо, чтобы числитель и знаменатель переполнялись как можно медленнее.
Число во входных данных имеет не более двух знаков после запятой.
Если умножить такое число на 100, получим целое число.
Поэтому можно обойтись без вещественных чисел.
И никаких проблем с точностью и эпсилоном нет.
Только вот погрешность может случиться уже в процессе чтения (числа с плавающей точкой). И посему суперважно: если на паскале, то превращать в целое именно через round(x*100), а ни в коем случае не trunc(x*100) и не int(x*100); если на C/C++, то всё-таки прибавлять к 100*x или 0.5, или малое эпсилон, это уж (благодаря тому что знаем сколько знаков после точки) без разницы.
Можно прочитать то, что слева от точки как одно целое число, а то, что справа от точки — как другое.
Прочитать отдельно одно отдельно другое — это как-то не "умножить так**ое** числ**о** на 100". А о том, что можно прочитать отдельно, я уже писал (может, именно этот способ был упомянут не совсем чётко, но под "читать сразу целые числа" я имел в виду именно его)