There are N points cooridinate is x[1],x[2]....x[N]; try to partition these points into two sets {p1,p2,....pk1} (q1,q2,...qk2};p1<p2<..<pk1,q1<q2<..<qk2 the weight of partion w=abs(xp1)+abs(xp2-xp1)+abs(xp3-xp2)...+abs(xpk1-xp(k1-1)+abs(xq1)+abs(xq2-xq1)+...+abs(xqk2-xq(k2-1)).
find the kth smallest partion.. N<=10000, K<=500000, x[i]<=100000000..
you can submit this problem here:
http://www.lydsy.com/JudgeOnline/problem.php?id=3945
two partions are different if and only if the sets of them are different..
Time Limit: 20 Sec
Really?
Yes, time limit is too tight,I have solved this problem in K*lg(n)^2+n*log(n)^2+k*lg(n)
and set the first k==min(k,200),and get Accepted..
Even if K = 500000, Your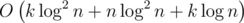
algorithm should run in less than 1 sec!
How did you do it? I have seen many problems that seem unsolvable, but this one is completely unapproachable. Your complexity is really good and should easily fit in 2-3 second. Maybe that strange judges's grader is just too slow. Could you, please, briefly describe the solution? Something like N^3 would be easy and I hardly found an NlogN algorithm to get the smallest weight. But, as I see from your complexity, you're somehow binary searching the answer which I have no clue how to include in my dynamic programming (the only way I know to get the smallest weight, let alone the Kth)
first ,try to find the minimum distance of every state i, optimal way to partion first i points
into two sets using dynamic programing:
dist[0][i]=min(dist[0][j]+abs(x[j+2]-x[j+1])+abs(x[j+3]-x[j+2])+..+abs(x[i]-x[i-1])+abs(x[i+1]-x
[j]); we can write abs(x[j+2]-x[j+1])+abs(x[j+3]-x[j+2])+..+abs(x[i]-x[i-1])
as sum[i]-sum[j+1],by precompute sum[i]=abs(x[1])+abs(x[2]-x[1])+..+abs(x[i]-x[i-1]);
so dist[0][i]=min(dist[0][j]+sum[i]-sum[j+1]+abs(x[i+1]-x[j]);
we can use segment_tree to optimal this dynamic programing process in
N*log(N).
and similarly we should compute the reverse state dist[1][i] means partition points i,i+1,...n
into two sets...
now we'll focus on Kth smallest partitions:
Do you know the O((m+k)*log(n)) algorithm on K th shortest paths??
if you don't find it on the internet, it is a Classical problem(solutions)..
but there is a problem.. m is about O(n^2) how to optimize?
we can thoose the first K smallest edges: by smallest we mean the weight:
w[i][j]= dist[0][i]+dist[1][j]+sum[j+1]-sum[i]+abs(x[j]-x[i]) : ie minimum distance go to i and using edges (i,j) to get to point j,and from j to destination point..
we want to find the Kth smallest edges, I using binary search weight and find how many edges is
smaller than this weight and record them, it can be done in K*log(w)*log(n)..
at last you can use these K edges to run kth smallest shortest path in k*log(n)
you can try to smaller these K number because for many tests the edges you are truly used is far
smaller than K
Could you please provide a link or a formal name to look for (for the algorithm). I don't know it and it seems is has a really good complexity. I'd be happy if you could give me a problem to solve too (like the classical problem asking for the exact same thing as the algorithm you mentioned). I can't believe I missed this one, I thought I know most of them. After that, I see how you can build a graph and optimizing it should be something I can handle myself (maybe I could even come up with a slightly different solution that could help you too).
here is the article
http://pan.baidu.com/share/link?uk=1176019800&shareid=3271123889&fid=848270619&errno=0&errmsg=Auth%20Login%20Sucess&&bduss=&ssnerror=0
but it is in Chinese,try to translate it..
the original Kth shortest path problem is here:
http://codeforces.me/gym/101365
problem I..
Thank you! Once I understand the algorithm and solve this problem, I'll come back to the one you've mentioned in this blog and would try to solve it. If I find any better solution, I'll let you know
Pretty sure this is Eppstein's algorithm.
That's exactly what I just started to read a couple of minutes ago. Thanks! At least now I'm sure I am reading in the right place
So I have another idea of building the graph. The complexity would be approximately the same, but the Klog^2(N) term disappears. I build a graph with O(NlogN) nodes and O(NlogN) edges: N nodes for the positions in the array and NlogN for the nodes in a persistent segment tree. The paths in the graph ending at a position should have a length equal to the unoptimal dp if you chose a certain partition so far. The paths will go from a position to some node in the persistent segment tree and back to some other position and so on. Basically we add edges instead of actually finding the smallest distance. Edges from positions to nodes in the segment tree when we update and vice versa when we query. It must be persistent to assure that we don't get from a position i to some other smaller position j. This way, once you have the graph built, you can simply run the classical algorithm and the only part that depends on K would be the KlogK. I know it's not really well explained, mainly because I should've better define unoptimal dp. It is just some cost that you can achieve till some position by using the same recurrence, the only change being that now you don't have to use minimum of something, but rather the reunion of those possible values.
Ohh and, of course, to reduce logVmax to logN (from the segment tree part because we update and query depending on values of X), we just need to use a normalization.