I need help in the problem : problem B — center
Someone please share idea on how to solve it.
Thanks
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 164 |
| 1 | maomao90 | 164 |
| 3 | Um_nik | 163 |
| 4 | atcoder_official | 160 |
| 5 | -is-this-fft- | 158 |
| 6 | adamant | 157 |
| 6 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 8 | nor | 154 |
| 10 | djm03178 | 153 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Nov/13/2024 06:15:30 (k3).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










Note : When weight is 1.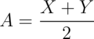 and
and 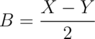 .
. 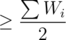
You can do the transformation from X = A + B and then Y = A - B, then
Now, we can see that doing this max(X - Xi, Y - Yi) = max(A' - Ai + B' - Bi, A' - Ai - (B' - Bi)) [where A', B' are the transformations for center given in the problem]. Now we can see that this value is nothing but |A' - Ai| + |B' - Bi|. So this effectively means that we have to find the median of A's, B's independently.
When weight is not necessarily one, what we can do is multiply it by 100 as it given that it's accurate upto 2 decimal places, and can make a pair array of < Ai, Wi > , sort it and using find the prefix sum, find the first i where prefix sum(i) is
I know there are 2 approaches:
Do 2 ternary searches. The outer for x coordinate and the inner for y (or vice versa).
Transform the Chebyshev distance to Manhattan distance by rotating and scaling. The find the answer in Manhattan distance. Actually, it is the median, and in the large dataset it is the weighted median.
I used the second approach the solve both cases in the real contest.
Can you share the code for the second approach? I got WA using the 2nd one on large dataset during the contest.
https://ideone.com/IYRunA