Let's discuss problems.
B is very nice. Until the end of the contest, I thought it was a marathon task. Then yutaka1999 told me the following: for an odd prime p, a[p] = 2 - p%4.
And I like geometry tasks like J.
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
Let's discuss problems.
B is very nice. Until the end of the contest, I thought it was a marathon task. Then yutaka1999 told me the following: for an odd prime p, a[p] = 2 - p%4.
And I like geometry tasks like J.
| Название |
|---|



For B, I have found an article which says, that if we take any odd prime q, and get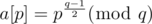 (which is always +1 or -1, except for p = q, where we force a[q] = 1), maximum of prefix sum have order of logn. You do same for q = 4. 4 seems to be not odd or prime. But it still works.
(which is always +1 or -1, except for p = q, where we force a[q] = 1), maximum of prefix sum have order of logn. You do same for q = 4. 4 seems to be not odd or prime. But it still works.
For example, for q = 3, it's just -1 for primes of form 3k + 2, and 1 for all others. We got ok with that one.
We are sorry that the paper was so easy to find, I didn't manage to google it myself. I wonder if many of the teams used google to solve this problem?
we managed to find this solution. for and prime p, try to put 1, and calculate balance on the prefix, if absolute value of balance is more then 20, change value of the last prime, and recalculate balance.
Is there any theoretical proof to the construction instead of verifying with a program?
Claim: for f(p) = - 1 with p = 3k + 2, and f(p) = 1 for all the rest, the value of f(1) + ... + f(n) is the number of ones in the ternary expansion of n.
I am surprised that so many people came up with such hideous construction.
What's the solution of A/E/F/H?
Several teams i know got local optimisations + precalc
A: centroid tree of centroid tree is this tree. For others — probably not.
H: binary search for get distances from random point. There are not too many points with such distance. Check them all
F:
Let's build suffix automaton for both strings. Also for both strings we will count longest suffix, which is in other string. Lcs is maximum of length of this suffixes over history before current moment.
How to recalc it.
1. Automaton is online algorithm, symbol just can be add.
2. For suffixes of string for which symbol is added, we need just move by edge of other automaton. If we have no move, we go by link, and length is now max_len for new vertex. The only trick here — if state we are placed in should be divided, we need to move to cloned state or not, depending on our length and splitting length
3. For string, we add symbol, there are two possibilities. Nothing will happen, or new longest suffix of other string is suffix of this string too. We can find longest such suffix using hashing and binary search. If it's longer, than state we have, we should move to this length and vertex just added to automaton (vertex corresponding to this suffix is new, because it didn't appeared in string before, because it's longer, that longest suffix we had).
I also assumed, centroid tree's centroid tree is same. But that is not true. Suppose:
Given tree: 3-2-4-1. Centroid tree: (2(3)(14)) -> 3-2-1-4 Again centroid tree: (1(23)(4))
So the root changed from 2 to 1. So if this tree is subtree of another tree (Suppose there is: 5-2 and 5-[6, 10] in the original tree), then the centroid (aka root) of this subtree (3-2-1-4) changed from 2 to 1 when we took centroid tree again. So centroid tree's centroid tree is not same?
H: Let's choose two random points (we used (0, 0) and (1, 0)). We can find all interesting circumferences (that is, circumferences containing at least one point) centered in each of these two points using binary search.
After that, we can check all intersection points of circumferences for the first and for the second center that have integer coordinates (I don't know a theoretical upper bound on the number of such points, but apparently it's pretty small).
For B we didn't come up with any nice construction so we solved it with randomization + greedy + some local optimization: basically move from left to right, assign primes with either +1 or -1 randomly, once you got too big balance — try to change some recent +1 prime to -1, once you got too small balance — try to change some recent -1 to +1.
E: Our solution is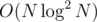 but is very close to TL, so I'm not sure this was intended.
but is very close to TL, so I'm not sure this was intended.
Let l(i, k) and r(i, k) be the leftmost and rightmost trampolines reachable given that you start at location I and use exactly 2k jumps. There are distinct values to compute and each one can be computed in
distinct values to compute and each one can be computed in  if you maintain min/max range trees on the l and r values from the previous level for
if you maintain min/max range trees on the l and r values from the previous level for 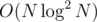 precomputation.
precomputation.
With all of these precomputed, you can binary search for the answer in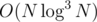 time naively because it takes
time naively because it takes 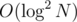 time to compute for a specific starting location the range given the l and r values. To cut off a logarithmic factor, instead of binary searching directly, maintain the ranges explicitly and attempt to lift the answer by powers of two in decreasing order — this removes a logarithmic number of range tree queries and is therefore.
time to compute for a specific starting location the range given the l and r values. To cut off a logarithmic factor, instead of binary searching directly, maintain the ranges explicitly and attempt to lift the answer by powers of two in decreasing order — this removes a logarithmic number of range tree queries and is therefore. 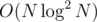 .
.
We are in the process of writing the editorial for the contest, which we will share here (probably soon after the Codeforces contest ends).
The link can be found in this post. Thanks for waiting!
How to solve problem J?
I liked J a lot. Suppose the box is reguler m-gon, and the cake is n-gon. Let's solve the problem from opposite direction. If the box is of size 1, what is the largest cake? Suppose the distance of a vertex of cake, from center is d. Draw the circle. It will intersect the box in several places. From there you can deduce some condition like: "this angle to this angle forbidden region for a cake's vertex, next this part allowed, ...". If you play a bit, you will figure out because of symmetry these angular gaps are equal, I mean its like: "t1, t2, t1, t2 ..." where t1+t2 = 2pi/m (suppose t1 is allowed and t2 is forbidden). If you think a bit, you will understand, for all the vertex angles of the cake MODULO (t1+t2) has to be in [0, t1]. We can always put a vertex of the cake at 0, so: all the other vertex are at: i*2pi/n for i = [0, n — 1]. To make the cake biggest, we actually need to find out the largest value of i*2pi/n mod 2pi/m, now if you play around a bit, you will find that for this i, mi mod n is the largest. Say g = gcd(m, n) and m'=m/g, n'=m/g. Then largest mi mod n = g(n'-1). Now go back and use this value along the chain to figure out the largest cake size.
Sorry for not so clear description, but this is how I solved it.
Where I can find these problems?