Techkriti 2017 and samsung research India brings forward International Online Programing Contest (IOPC) with a chance to grab your pile from INR 1,20,000. This is a rated contest of 3 hrs and will start at 15:00 IST on the 21st of April,2017. There is a little under 12 hours left till the contest starts.
The contest is hosted on codechef.
Contest page : https://www.codechef.com/IOPC2017.
Note that the contest is an individual rated contest on Codechef.
The problem setters are utkarshl, kaushal02 and dwivedi with triveni and Dopahkiin as testers.
The prize distribution is as follows:
1.The international first,second and third get 20%,17% and 13% of total money respectively.
2.The 4th and 5th positions (international) get 10% & 8% respectively. positions 6-10 get 1.6% each.
3.The first, second and third in India get 10,8 and 6 percentage of total
4. In case if someone is eligible for more than 1 prize, he gets the larger one only.
Hoping for a huge response from everyone. May the Force be with you!











Auto comment: topic has been updated by ajs97 (previous revision, new revision, compare).
We have not received the prize money from IOPC 2015.
The codechef contest drop down list says Techkranti — IOPC 2017. xD
Where does this fail for this problem ? I just simulated everything using segment tree.
segment tree is not required.Its just basic recursion. Its a variant of standard version of Josephus problem.
get_ac function takes int k, while it overflows in main — various similar mistakes like this. I just simulated everything using BIT and it worked fine.
Nothing would overflow. i have #define int long long in the code.
How to solve Christmas Time?
Read up on [Partition Function](https://en.wikipedia.org/wiki/Partition_(number_theory)#/Generating_function). You can calculate P(n) in O(sqrtN) using generalized pentagonal numbers. Then query for N, M reduces to range product of P(i), for i over the range [M, M+N-1] which you can do in O(1). Overall time complexity is O(NsqrtN + Q).
Let A(n) be the number of ways to distribute n sweets . Then A(n) = A(n - 1) + A(n - 2) - A(n - 5) - A(n - 7).... i.e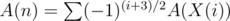 where X(i) is the ith pentagonal number. Rest is just building prefix product of this array.
where X(i) is the ith pentagonal number. Rest is just building prefix product of this array.
My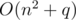 solution with
solution with 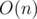 space complexity passed in Java. Was this expected or the time limit was bit too relaxed for Java?
space complexity passed in Java. Was this expected or the time limit was bit too relaxed for Java?
Can someone please explain the approach for https://www.codechef.com/problems/IOPC17G/
See this code — https://www.codechef.com/viewsolution/13376017
If the intervals intersect, it is the right end point of the interval that ends first. Else, let [a,b] be the first interval and [l,r] the second with b<r. Consider the naive solution of checking every number from b to 1 in decreasing order. What is the condition for a given x? It is that a multiple of x lies both in [a,b] and [l,r] => (a-1)/x<b/x and (l-1)/x<r/x. Now, consider x' such that x' = x-1 and b/x = b/x' and r/x = r/x' then (a-1)/x'>=(a-1)/x, so there is no need to check x'. So from a given x we need to check only next smaller number x' such that b/x' or r/x' is different. This is a major optimization since there are only O(sqrt(r)) different r/x. So, from a given x next x' = max(r/(r/x+1),b/(b/x+1)). Complexity = O(sqrt(r)) for a test case.
Thanks.