One of my friend recently asked me the following problem:
"Given an array a1, a2, ..., an and a number K (n ≤ 105, ai ≤ 109). Is there a way split the array into K disjoint sub-arrays (don't have to be contiguous) such that sum of each sub-array is equal to each other (and equal to 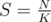 )?"
)?"
My teacher came up with the following greedy solution: for each sub-array, keep choosing the maximum number such that sum of sub-array with that number is still smaller or equal to S. When it's impossible to add more number from a to this sub-array, check if the current sum is equal to S.
However, both my teacher and me are unable to neither prove the correctness of the solution nor find a counter-example for it. Is this greedy solution always optimal? How to prove (or disprove) it? Thanks in advance.










That greedy is wrong — same reason why you can't do knapsack greedily
n = 6, k = 2 sum = 48
2 2 4 5 17 18
you will find 18 5 and terminate.
I guess that problem is np complete.
Thanks for pointing out the counter example.