The first problem I will be discussing here, is "Plant", where a group of dwarves planted a very interesting recursive plant!! (Maybe the dream of any housewife? :p )

• Solution's "entangled" recursive behaviour

More formally, we have a triangle, that on each new year is filled with one triangle on its inside, according to the following rules:

• If the triangle is pointing up, it's filled with one triangle pointing down, now having 3 smaller triangles upwards and one triangle downwards.

• If the triangle is pointing down, it is filled with one triangle pointing up, now having 3 smaller triangles downwards and one triangle upwards.

These two rules will be the basis to build our solution.

Let's denote as f(U, n) the number of upwards and downwards triangles that will be generated, if starting from year n with an upwards triangle and similarly f(D,n) the number of upwards and downwards triangles generated if we start on year n, with a downwards triangle.

We now see that, if we start on year 1, with both an upwards triangle and a downwards triangle, we will get:

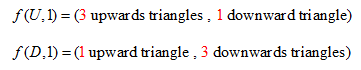
obviously, by this notation, the answer to the original problem will be f(U,n-1) (we start on year n-1, and finish at year n, and will only count the number of upwards triangles there)

• Assembling the matrix and understanding the exponentiation

So, as we can see there's more to this problem than a simple recursive relationship, as the number of up and down triangles after n years will depend on eachother's values. Fortunately, we have a very powerful tool on our arsenal as programmers which is matrix manipulation and more specifically, matrix exponentiation.

As we identified the need of using a matrix to modelate our system initial state, it follows naturally that matrices will need to be used to simulate the evolution (on this case the plant growth rate) of it as well.

Our matrix can be assembled by merging the numbers highlighted in red above, so:

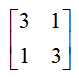
will be the matrix that will model our system and allow us to get a solution, as now it's only a matter of computing the Nth power of this matrix to obtain the answer!!

• Implementation of the idea on a programming language

To implement our idea, we now need to apply any algorithm we know of that does matrix exponentiantion, but, for n as large as 1000000000000000000, a naive exponentiation algorithm won't run in time, and the trick is to use the generalized form of exponentiation by squaring applied to matrices, which can be seen here (more information about the original method extended with modular exponentiation can be found on "Introduction to Algorithms" by Cormen, Leiserson, Rivest & Stein, p.879, Chapter 31, 2nd edition).

Now, to show the implementation, I decided to use Python, as there was an already coded fast exponentiantion algorithm on a GCJ editorial (Round1A 2008), and also, because I think that the Python code is more readable and more suitable for tutorial purposes:

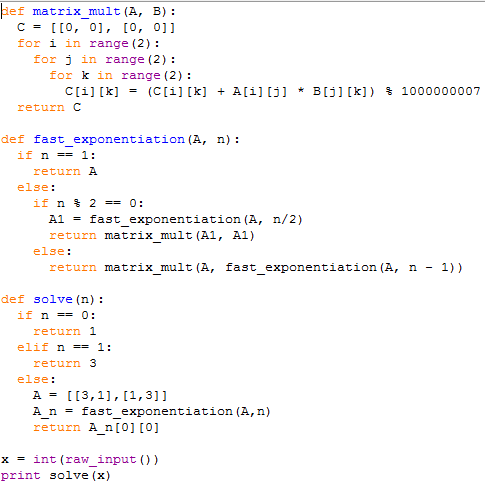
• Final remarks

My next goal now, is to be able to replicate this code on C++, in order to get better and better!!

Also, this was my first "editorial" here, I am not sure if you liked it, if it was too long, confuse, etc, etc, but as this is a work in progress any critics and new ideas for future posts will be welcome!

Best regards,

Bruno