Hello everyone!
I was solving a problem (from a Bulgarian competition) which is about the game Lights Out — https://en.m.wikipedia.org/wiki/Lights_Out_(game). In the problem you are given a NxM table (N*M<=1000) — the initial configuration of the game. You whant to make all the cells equal to zero. You should print a way to do this.
The problem can be solved with meet in the middle and bitmask dp, with the given constraints. Another way is using Gauss elimination modulo 2 with N*M equations for each cell. But this approach is O((N * M)3). It actually can be reduced to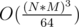 
with a bitset.
In the editorial of the problem it is said that there exists a solution for much larger data — N,M<=500, using Gauss elimination but it isn't explained. If someone knows it can he/she explain it. I will appreciate your help!
It is enough to fix the configuration of the first row. The configuration of the second is uniquely determined and than, you can assure that line i is ok by fixing line i + 1 with already fixed line i — 1. So after these operations, you have for each cell on the last row, a way of obtaining it out of cells on the first row. Now, you are sure that all the lines up to N — 1 have the lights in the desired configuration, so all it remains is to assert that the last line verify the conditions. So you'll have a N equations system with N values to be determined(the values on the first line). For obtaining the configuration of each cell (including internal ones), based on the first line you can keep just the last 3 lines configurations and get O(N^3) time complexity. The gauss is O(N^3) as well, and for both of them you can use bitset to get a 1/64 constant.